Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao
Câu hỏi:
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB = 2a. Thể tích khối tứ diện OO'AB theo a là:
A. \(V = \frac{{\sqrt 3 {a^3}}}{8}\)
B. \(V = \frac{{\sqrt 3 {a^3}}}{4}\)
C. \(V = \frac{{\sqrt 3 {a^3}}}{6}\)
D. \(V = \frac{{\sqrt 3 {a^3}}}{{12}}\).
Trả lời:
Đáp án đúng là: D
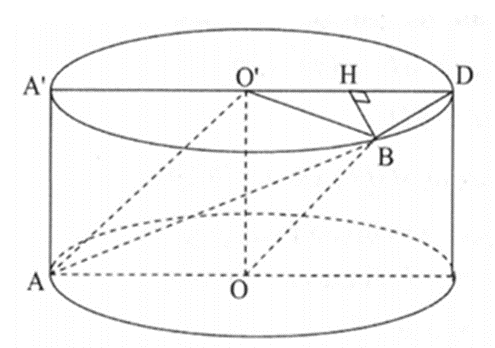
Kẻ đường sinh AA’. Gọi D là điểm đối xứng A’ qua O’ và H là hình chiếu của B trên đường thẳng A’D
Ta có \(\left\{ \begin{array}{l}BH \bot A'D\\BH \bot {\rm{AA'}}\end{array} \right. \Rightarrow BH \bot \left( {AO{\rm{O}}'A'} \right)\)
Vì tam giác ABA’ vuông tại A’ nên theo định lý Pytago có:
\(A'B = \sqrt {A{B^2} - A'{A^2}} = \sqrt {{{\left( {2{\rm{a}}} \right)}^2} - {a^2}} = a\sqrt 3 \)
Vì tam giác DBA’ vuông tại B nên theo định lý Pytago có:
\(BD = \sqrt {A'{D^2} - A'{B^2}} = \sqrt {{{\left( {2{\rm{a}}} \right)}^2} - {{\left( {a\sqrt 3 } \right)}^2}} = a\)
Mà O’B = O’D = a
Suy ra tam giác O’BD đều có BH là đường cao
Do đó \(BH = \frac{{a\sqrt 3 }}{2}\)
Diện tích tam giác AOO’ là: \[{{\rm{S}}_{AOO'}} = \frac{1}{2}OA.OO' = \frac{1}{2}{a^2}\]
Thể tích khối tứ diện OO'AB theo a là:
\(V = \frac{1}{3}.BH.{S_{AO{\rm{O}}'}} = \frac{1}{3}.\frac{{\sqrt 3 a}}{2}.\frac{{{a^2}}}{2} = \frac{{\sqrt 3 {a^3}}}{{12}}\)
Vậy ta chọn đáp án D.

