Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC, DB
Câu hỏi:
Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC, DB. Đường thẳng EF lần lượt cắt AB, CD tại H, K. Chứng minh rằng \(\widehat {KHB} = \widehat {HKC}\)
Trả lời:
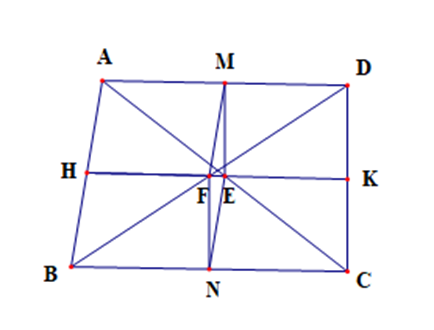
Gọi M là trung điểm của AD, N là trung điểm của BC
Xét tam giác ACD có M, E lần lượt là trung điểm của AD, AC
Suy ra ME là đường trung bình
Do đó ME // CD, \(ME = \frac{1}{2}C{\rm{D}}\) (1)
Xét tam giác BCD có N, F lần lượt là trung điểm của BC, BD
Suy ra NF là đường trung bình
Do đó NF // CD, \(NF = \frac{1}{2}C{\rm{D}}\) (2)
Xét tam giác ACB có N, E lần lượt là trung điểm của BC, AC
Suy ra NE là đường trung bình
Do đó NE // AB, \(NE = \frac{1}{2}AB\) (3)
Xét tam giác ABD có M, F lần lượt là trung điểm của AD, BD
Suy ra MF là đường trung bình
Do đó MF // AB, \(MF = \frac{1}{2}AB\) (4)
Từ (1), (2), (3) và (4) suy ra \(\left\{ \begin{array}{l}ME//NF//C{\rm{D}}\\MF//NE//AB\\ME = NF = \frac{1}{2}C{\rm{D}}\\MF = NE = \frac{1}{2}AB\end{array} \right.\)
Mà AB = CD nên NF = NE
Suy ra tam giác NFE cân tại N
Do đó \(\widehat {NF{\rm{E}}} = \widehat {{\rm{NEF}}}\)
Vì NE // AB nên \(\widehat {KHB} = \widehat {NEK}\) (hai góc đồng vị)
Vì NF // CD nên \(\widehat {HKC} = \widehat {NFH}\) (hai góc đồng vị)
Suy ra \(\widehat {KHB} = \widehat {HKC}\)
Vậy \(\widehat {KHB} = \widehat {HKC}\).

