Cho hình trụ có chiều cao bằng 2a và diện tích xung quanh là πa^2. Bán kính
Câu hỏi:
Cho hình trụ có chiều cao bằng 2a và diện tích xung quanh là π. Bán kính đáy của hình trụ là:
A.
B.
C.
D.
Trả lời:
Đáp án D
Từ giả thiết ta có:
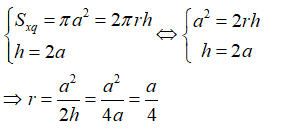
Câu hỏi:
Cho hình trụ có chiều cao bằng 2a và diện tích xung quanh là π. Bán kính đáy của hình trụ là:
A.
B.
C.
D.
Trả lời:
Đáp án D
Từ giả thiết ta có:
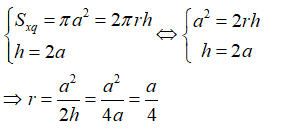
Câu 1:
Tam giác ABC vuông cân đỉnh A có cạnh huyền là a. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo thành hình nón (N). Diện tích xung quanh của hình nón (N) là:
Câu 2:
Hình nón (N) có đường sinh gấp hai lần bán kính đáy. Góc ở đỉnh của hình nón là:
Câu 3:
Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng:
Câu 4:
Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được:
Câu 5:
Cho khối trụ có diện tích toàn phần 5π và bán kính đáy là a. Thể tích khối trụ là:
Câu 6:
Hình trụ (H) có diện tích toàn phần là 8π(c) và thể tích khối trụ là 3π(c). Tính chiều cao của hình trụ ta được bao nhiêu kết quả?
Câu 7:
Hình trụ (H) có tỉ số diện tích xung quanh và diện tích toàn phần là 1/3. Biết rằng thể tích khối trụ là 4π. Bán kính đáy của hình trụ là:
Câu 8:
Ta dùng hai hình chữ nhật có cùng kích cỡ để làm thành hai hình trụ (H1) và (H2) bằng cách quay các hình chữ nhật đó, lần lượt theo chiều dài và chiều rộng. Tỉ số hai diện tích xung quanh hình trụ (H1) và hình trụ (H2) là:
