Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều
Câu hỏi:
Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều cạnh a và nằm trên hai mặt phẳng vuông góc với nhau. Bán kính mặt cầu ngoại tiếp hình tứ diện là:
A.
B.
C.
D.
Trả lời:
Đáp án D
Gọi H là trung điểm của CD. Khi đó ta có AH ⊥ (BCD), BH ⊥ (ACD). Gọi P, Q lần lượt là tâm của các tam giác đều BCD và ACD. Dựng hình chữ nhật HPIQ thì nó là hình vuông và I là tâm mặt cầu ngoại tiếp tứ diện. Khi đó ta có bán kính mặt cầu là 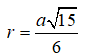
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao a.
Xem lời giải »
Câu 2:
Hình trụ (H) có diện tích xung quanh là 6π(c) và thể tích khối trụ là 9π(c). Chiều cao của hình lăng trụ là:
Xem lời giải »
Câu 3:
Cho hình nón tròn xoay có đường cao 12cm và đường kính đáy 10cm. Độ dài đường sinh của hình nón là:
Xem lời giải »
Câu 4:
Một hình nón có đường kính đáy là 2a, góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a.
Xem lời giải »
Câu 5:
Cho hình chóp tam giác đều S.ABC, mặt phẳng (SBC) tạo với đáy một góc bằng 30o và SA = 2a. Thể tích khối cầu ngoại tiếp hình chóp S.ABC là:
Xem lời giải »
Câu 6:
Một cái tháp khổng lồ có thân là hình trụ và mái là một nửa hình cầu. Người ta muốn sơn toàn bộ mặt ngoài của tháp (kể cả mái). Tính diện tích S cần sơn (làm tròn đến mét vuông).
Xem lời giải »