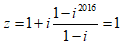Cho số phức z thỏa z = 1+ i+ i^2+ i^3+...+ i^2016. Khi đó phần thực và phần ảo của z lần lượt là

Câu hỏi:

Cho số phức z thỏa z = 1+ i+ i²+ i³+...+ i²⁰¹⁶. Khi đó phần thực và phần ảo của z lần lượt là

A. 0 và -1.

B. 0 và 1.

C. 1 và 1.

D. 1 và 0.

Trả lời:

Chọn D.

Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = i .

Do đó :

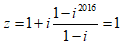
Vậy phần thực và phần ảo của z là 1 và 0.

Câu 1:

Cho số phức z = ( 3 - 2i)(1 + i) ² . Môđun của $w = i z + \bar{z}$ là

Câu 2:

Cho số phức z thỏa mãn điều kiện $(2 + i) z + \frac{1 - i}{1 + i} = 5 - i$ . Môđun của số phức W = 1 + 2z + z² có giá trị là:

Câu 3:

Cho số phức z = -3 + 2i. Tính P = |z + 1 – i|.

Câu 4:

Cho hai số phức z₁= 3 - 2i; z₂= -2 + i Tính P = | z₁ + z₂|.

Câu 5:

Giá trị của biểu thức S = 1+ i²+ i⁴+ ...+ i^4k là

Câu 6:

Cho số phức z = 1+ ( 1+ i) + ( 1+i) ²+ ...+ (1+ i) ²⁶ . Phần thực của số phức z là

Câu 7:

Cho số phức z = x + y.i thỏa mãn z³ = 2 - 2i. Cặp số là(x;y)

Câu 8:

Cho số phức z = 3 + i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:

Các dạng bài tập Toán lớp 12