Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho

Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho $\overrightarrow{BH}=\frac{1}{3}\overrightarrow{HC}$. Điểm M di động nằm trên BC sao cho $\overrightarrow{BM}=x\overrightarrow{BC}$. Tìm x sao cho độ dài của $\overrightarrow{MA}+\overrightarrow{GC}$ đạt giá trị nhỏ nhất.

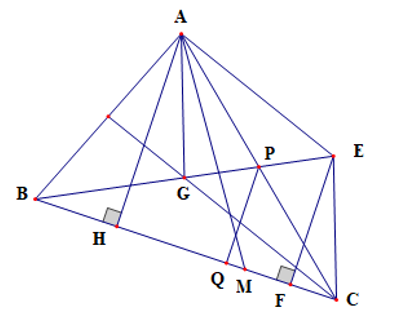
Dựng hình bình hành AGCE

Ta có: $\overrightarrow{MA}+\overrightarrow{GC}=\overrightarrow{MA}+\overrightarrow{AE}=\overrightarrow{ME}$

Kẻ EF ⊥ BC (F ∈ BC)

Khi đó $\left|\overrightarrow{MA}+\overrightarrow{GC}\right|=\left|\overrightarrow{ME}\right|=ME\ge EF$

Do đó $\left|\overrightarrow{MA}+\overrightarrow{GC}\right|$ đạt giá trị nhỏ nhất khi M ≡ F

Gọi P là trung điểm của AC, Q là hình chiếu vuông góc của P lên BC

Vì AGCE là hình bình hành, P là trung điểm của AC

Suy ra P là trung điểm của GE

Do đó $GP=PE=\frac{1}{2}GE$

Vì G là trọng tâm tam giác ABC, BP là trung tuyến

Suy ra $BG=\frac{2}{3}BP,GP=\frac{1}{3}BP$

Ta có: BE = BP + PE

Hay $BE=BP+\frac{1}{3}BP=\frac{4}{3}BP$

Xét ∆BPQ và ∆BEF có

$\widehat{FBE}$ là góc chung;

$\widehat{BQP}=\widehat{BFE}=90°$

Suy ra: ∆BPQ ∽ ∆BEF (g.g)

Do đó $\frac{BP}{BE}=\frac{BQ}{BF}=\frac{3}{4}\Rightarrow \overrightarrow{BF}=\frac{4}{3}\overrightarrow{BQ}$

Xét DAHC có P là trung điểm của AC và AH // PQ (vì cùng vuông góc với BC)

Suy ra Q là trung điểm của CH

Hay $\overrightarrow{HQ}=\frac{1}{2}\overrightarrow{HC}$; mà $\overrightarrow{BH}=\frac{1}{3}\overrightarrow{HC}$

Ta có: $\overrightarrow{BQ}=\overrightarrow{BH}+\overrightarrow{HQ}=\frac{1}{3}\overrightarrow{HC}+\frac{1}{2}\overrightarrow{HC}=\frac{5}{6}\overrightarrow{HC}=\frac{5}{6}.\frac{3}{4}\overrightarrow{BC}=\frac{5}{8}\overrightarrow{BC}$

Do đó: $\overrightarrow{BF}=\frac{4}{3}\overrightarrow{BQ}=\frac{5}{6}\overrightarrow{BC}$

Vậy $x=\frac{5}{6}$.