Cho tam giác ABC, D là trung điểm AB, E là trung điểm AC
Câu hỏi:
Cho tam giác ABC, D là trung điểm AB, E là trung điểm AC. Vẽ F sao cho E là trung điểm DF. Chứng minh:
a) DB = CF.
b) ∆BDC = ∆FCD.
c) DE // BC và .
Trả lời:
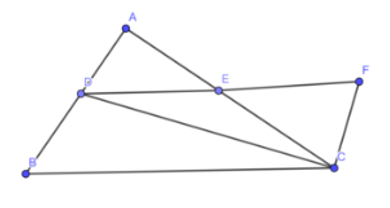
a) Xét tam giác AED và CEF có:
EA = EC
(đối đỉnh)
ED = EF
⇒ ∆AED = ∆CEF (c.g.c)
⇒ DA = CF
Mà DA = DB nên DB = CF
b) ∆AED = ∆CEF nên:
Suy ra: AB // CF
⇒ (so le trong)
Xét tam giác BDC và FCD có:
DC chung
BD = CF
⇒ ∆BDC = ∆FCD (c.g.c)
c) ∆BDC = ∆FCD nên
Suy ra: DE // BC (2 góc so le trong bằng nhau)
Lại có BC = DF = 2DE
Nên: .


