Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài .
Câu hỏi:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài .
Trả lời:
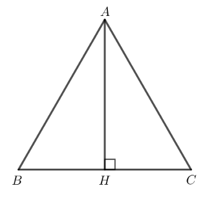
AH là đường cao vừa là đường phân giác nên
Hay
Lại có:
Suy ra: .
Câu hỏi:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài .
Trả lời:

AH là đường cao vừa là đường phân giác nên
Hay
Lại có:
Suy ra: .
Câu 1:
Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho . Điểm M di động nằm trên BC sao cho . Tìm x sao cho độ dài của đạt giá trị nhỏ nhất.
Câu 4:
Cho tam giác ABC có góc C nhọn, AH và BK là hai đường cao, HK = , diện tích tứ giác ABHK bằng 7 lần diện tích tam giác CHK. Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng?
Câu 6:
Cho tam giác ABC đều có cạnh bằng . Gọi M là trung điểm của AC. Tính độ dài vectơ .
Câu 7:
Cho tam giác ABC, điểm D đối xứng vs A qua B, E đối xứng B qua C, F đối xứng C qua A Gọi G là giao điểm của đường trung tuyến AM. Trong tam giác ABC với trung tuyến DN của tam giác DEF Gọi I, K lần lượt là trung điểm của GA và GD.
1) Chứng minh tứ giác MNIK là hình bình hành.
2) Chứng minh tam giác ABC và tam giác DEF có cùng trọng tâm.
Câu 8:
Cho tam giác ABC, đường trung tuyến AD. Gọi M là một điểm trên cạnh AC sao cho . Gọi O là giao điểm của BM và AD. Chứng minh rằng:
a, O là trung điểm của AD.
b, .
