Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu cùa H

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu cùa H lên AB và AC.

a) Chứng minh: AM.AB = AN.AC.

b) Chứng minh: $\frac{S_{A M N}}{S_{A C B}} = \sin^{2} B . \sin^{2} C$

Trả lời:

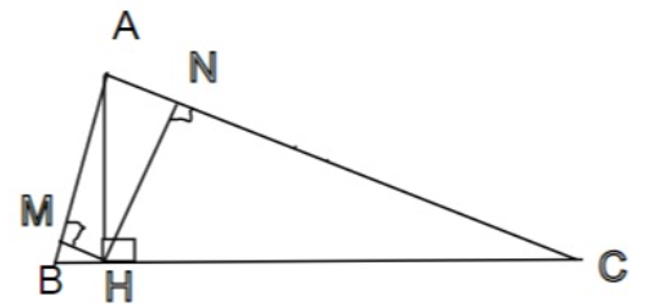
Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu cùa H (ảnh 1)

a) Có : AH là đường cao của tam giác ABC ⇒ $\hat{A H B} = 90 °$

Tam giác AHB vuông tại H có AM là đường cao

⇒ AM.AB = AH²

Tam giac AHC vuong tai H có AN là đường cao

⇒ AN.AC = AH²

Nên AM.AB =AN.AC

b) Tam giác AHB vuông tại H nên $\sin B = \frac{A H}{A B}$

Tam giác AHC vuông tại H ⇒ $\sin C = \frac{A H}{A C}$

Áp dụng công thức tính diện tích theo định lý sin, ta có:

Lại có: $S_{A B C} = \frac{1}{2} . A B . A C . \sin A$

$S_{A M N} = \frac{1}{2} . A M . A N . \sin A$

Suy ra: $\frac{S_{A M N}}{S_{A B C}} = \frac{\frac{1}{2} . A M . A N . \sin A}{\frac{1}{2} . A B . A C . \sin A} = \frac{A M . A N}{A B . A C} = \frac{A H^{2} . A H^{2}}{A B^{2} . A C^{2}} = {(\frac{A H}{A B})}^{2} . {(\frac{A H}{A C})}^{2} = \sin^{2} B . \sin^{2} C$