Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Câu hỏi:
Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Trả lời:
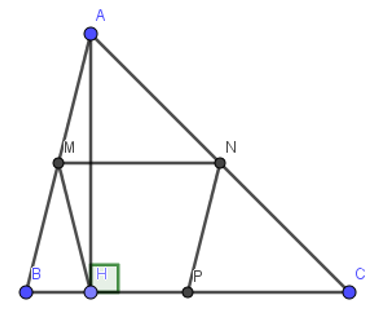
M, N lần lượt là trung điểm AB,AC nên MN là đường trung bình của tam giác ABC ứng với cạnh BC
⇒MN // BC hay MN // HP
⇒ MNPH là hình thang (∗)
Mặt khác:
Tam giác vuông ABH có HM là đường trung tuyến ứng với cạnh huyền nên (bổ đề quen thuộc)
⇒ Tam giác MHB cân tại M.
⇒
Mà (hai góc đồng vị với NP // AB)
⇒
⇒
Hay (**)
Từ (∗); (∗∗) ⇒ MNPH là hình thang cân (đpcm).


