Cho tam giác ABC vuông ở A, đường cao AH. Biết AH = 6cm và BC = 13cm. Tính AB, AC.
Câu hỏi:
Cho tam giác ABC vuông ở A, đường cao AH. Biết AH = 6cm và BC = 13cm. Tính AB, AC.
Trả lời:
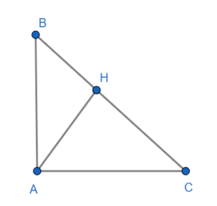
Ta có: AH2 = BH.CH = 62 = 36 (1)
BH + HC = BC = 13(cm) (2)
Thế (2) vào (1) ta có: (13 – HC).HC = 36
⇔ 13HC – HC2 – 36 = 0
⇔
Nếu HC = 9cm thì BH = 4cm
AB2 = BH.BC ⇒
AC =
Nếu HC = 4cm thì BH = 9cm
AB2 = BH.BC ⇒
AC = .


