Lý thuyết Nguyên hàm - Toán lớp 12

Lý thuyết Nguyên hàm

Tài liệu Lý thuyết Nguyên hàm Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về Nguyên hàm từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết

I. NGUYÊN HÀM VÀ TÍNH CHẤT

1. Nguyên hàm

    Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.

    Định lí:

    1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

    2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

    Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C

2. Tính chất của nguyên hàm

    Tính chất 1: (∫f(x)dx)' = f(x) và ∫f'(x)dx = f(x) + C

    Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.

    Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx

3. Sự tồn tại của nguyên hàm

    Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

4. Bảng nguyên hàm của một số hàm số sơ cấp

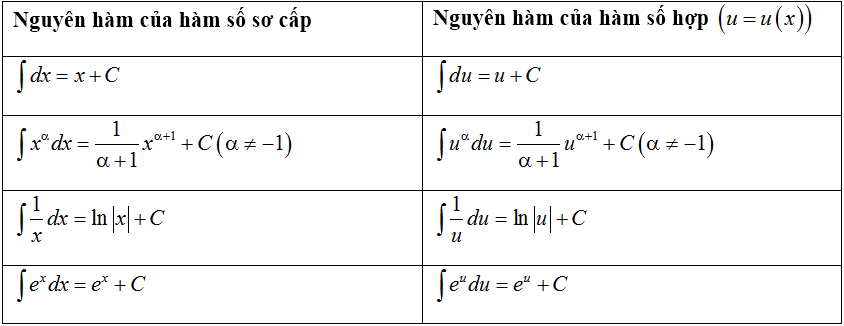
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM

1. Phương pháp đổi biến số

    Định lí 1: Nếu ∫f(u)du = F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì

    ∫f(u(x))u'(x)dx = F(u(x)) + C

    Hệ quả: Nếu u = ax + b (a ≠ 0) thì ta có ∫f(ax + b)dx = (1/a)F(ax + b) + C

2. Phương pháp nguyên hàm từng phần

    Định lí 2: Nếu hai hàm số u = u(x) và y = y(x) có đạo hàm liên tục trên K thì

    ∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dx

    Hay ∫udv = uv - ∫vdu

B. Kĩ năng giải bài tập

    - Tìm nguyên hàm bằng phương pháp biến đổi trực tiếp.

    - Tìm nguyên hàm bằng phương pháp đổi biến số.

    - Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần.