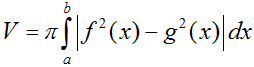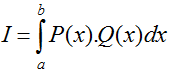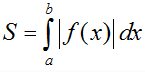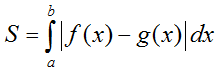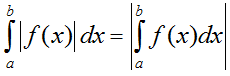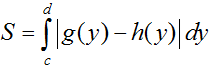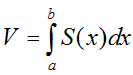Lý thuyết tổng hợp chương Nguyên hàm, Tích phân và ứng dụng - Toán lớp 12
Lý thuyết tổng hợp chương Nguyên hàm, Tích phân và ứng dụng
Tài liệu Lý thuyết tổng hợp chương Nguyên hàm, Tích phân và ứng dụng Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về Nguyên hàm, Tích phân và ứng dụng từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết
** NGUYÊN HÀM
1. Bảng nguyên hàm của một số hàm số sơ cấp

2. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
* Phương pháp đổi biến số
Định lí 1: Nếu ∫f(u)du = F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì
∫f(u(x))u'(x)dx = F(u(x)) + C
Hệ quả: Nếu u = ax + b (a ≠ 0) thì ta có ∫f(ax + b)dx = (1/a)F(ax + b) + C
* Phương pháp nguyên hàm từng phần
Định lí 2: Nếu hai hàm số u = u(x) và y = y(x) có đạo hàm liên tục trên K thì
∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dx
Hay ∫udv = uv - ∫vdu
** TÍCH PHÂN
1. Tính chất của tích phân
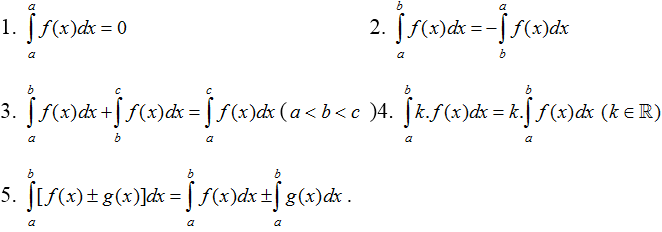
2. Một số phương pháp tính tích phân
Dạng 1: Tính tích phân theo công thức
Dạng 2: Dùng tính chất cận trung gian để tính tích phân
Sử dụng tính chất 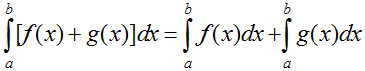
Dạng 3: Phương pháp đổi biến số
* Đổi biến số dạng 1
Cho hàm số f liên tục trên đoạn [a; b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên đoạn [a; b] và α ≤ u(x) ≤ β. Giả sử có thể viết f(x) = g(u(x))u'(x), x ∈ [a; b] với g liên tục trên đoạn [α; β]. Khi đó, ta có
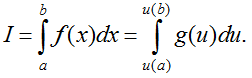
Dấu hiệu nhận biết và cách tính tính phân


* Đổi biến số dạng 2
Cho hàm số f liên tục và có đạo hàm trên đoạn [a; b]. Giả sử hàm số x = φ(t) có đạo hàm và liên tục trên đoạn [α; β](*) sao cho φ(α) = a,φ(β) = b và a ≤ φ(t) ≤ b với mọi t ∈ [α; β]. Khi đó:
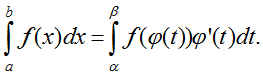
Một số phương pháp đổi biến: Nếu biểu thức dưới dấu tích phân có dạng
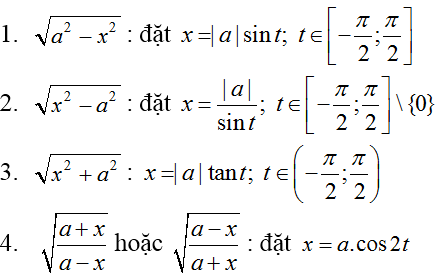
Dạng 4: Phương pháp tính tích phân từng phần.
Định lí : Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm và liên tục trên đoạn [a; b] thì
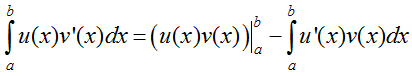
hay viết gọn là 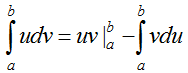
| Dạng hàm |
P(x): Đa thức Q(x): sin(kx) hay cos(kx) |
P(x): Đa thức Q(x): ekx |
P(x): Đa thức Q(x): ln(ax + b) |
P(x): Đa thức Q(x): 1/sin2x hay 1/cos2x |
| Cách đặt |
* u = P(x) * dv là Phần còn lại của biểu thức dưới dấu tích phân |
* u = P(x) * dv là Phần còn lại của biểu thức dưới dấu tích phân |
* u = ln(ax + b) * dv = P(x)dx |
* u = P(x) * dv là Phần còn lại của biểu thức dưới dấu tích phân |
Thông thường nên chú ý: “Nhất log, nhì đa, tam lượng, tứ mũ”.
** ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
1. Diện tích hình phẳng
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a, x = b được xác định:
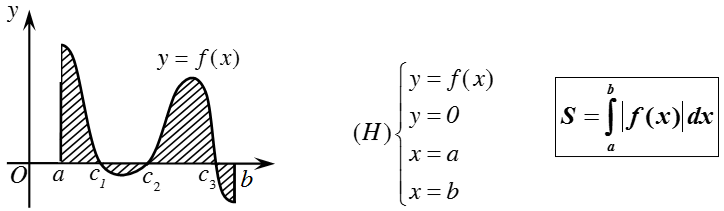
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a, x = b được xác định: :
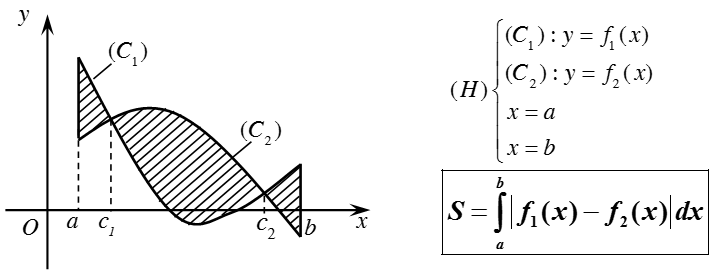
Chú ý:
- Nếu trên đoạn [a; b], hàm số f(x) không đổi dấu thì:
- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
- Diện tích của hình phẳng giới hạn bởi các đường x = g(y), x = h(y) và hai đường thẳng y = c, y = d được xác định:
2. Thể tích vật thể và thể tích khối tròn xoay
a) Thể tích vật thể:
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, (a ≤ x ≤ b). Giả sử S(x) là hàm số liên tục trên đoạn [a; b].
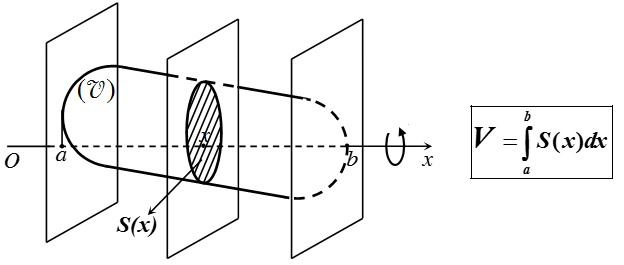
Khi đó, thể tích của vật thể B được xác định:
b) Thể tích khối tròn xoay:
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x) , trục hoành và hai đường thẳng x = a, x = b quanh trục Ox:
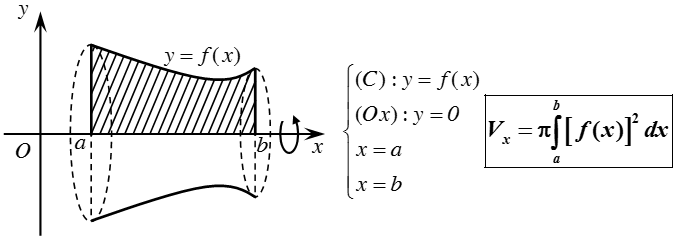
Chú ý:
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x = g(y), trục hoành và hai đường thẳng y = c, y = d quanh trục Oy:
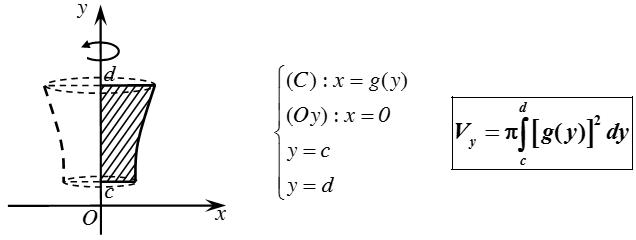
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x), y = g(x) và hai đường thẳng x = a, x = b quanh trục Ox: