Tập nghiệm của bất phương trình log 0,8 (x^2 +x) < log 0,8 (-2x+4)
Câu hỏi:
Tập nghiệm của bất phương trình là
A.
B.
C.
D. Một kết quả khác
Trả lời:
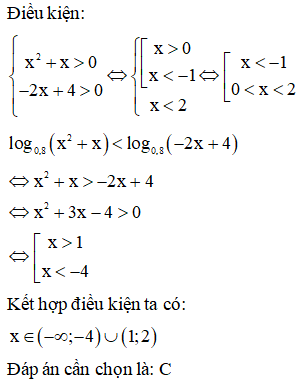
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
Xác định tập nghiệm S của bất phương trình
Xem lời giải »
Câu 4:
Bất phương trình có bao nhiêu nghiệm nguyên?
Xem lời giải »
Câu 5:
Tìm tập hợp nghiệm S của bất phương trình
Xem lời giải »
Câu 6:
Bất phương trình có bao nhiêu nghiệm nguyên?
Xem lời giải »
Câu 7:
Tìm tập nghiệm S của bất phương trình
Xem lời giải »
Câu 8:
Số nghiệm nguyên của bất phương trình là
Xem lời giải »
