Tập nghiệm của bất phương trình log 3 x nhỏ hơn hoặc bằng log 1/3 (2x)
Câu hỏi:
Tập nghiệm của bất phương trình là nửa khoảng (a;b]. Giá trị của bằng
A. 1
B. 4
C.
D. 8
Trả lời:
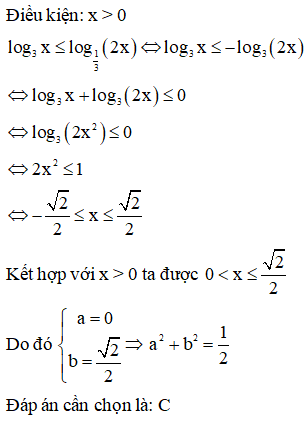
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tập hợp nghiệm của bất phương trình là
Xem lời giải »
Câu 2:
Tập nghiệm của bất phương trình có dạng S=[a;b]. Khi đó b-a bằng:
Xem lời giải »
Câu 3:
Số nghiệm nguyên dương của bất phương trình
Xem lời giải »
Câu 4:
Cho hàm số . Hỏi khẳng định nào sau đây là sai?
Xem lời giải »
Câu 5:
Bất phương trình có tập nghiệm là khoảng (a;b). Giá trị của 5b-a bằng:
Xem lời giải »
Câu 7:
Tập nghiệm của bất phương trình là . Khi đó ab bằng:
Xem lời giải »
Câu 8:
Cho hàm số y=f(x). Hàm số y=f’(x) có đồ thị như hình bên. Biết . Tìm tất cả các giá trị của m để bất phương trình nghiệm đúng với mọi

Xem lời giải »
