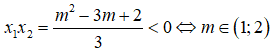Tìm m để hàm số y = -x^3 + (2m + 1)x^2 - (m^2 - 3m +2)x - 4 có cực đại, cực tiểu nằm
Câu hỏi:
Tìm m để hàm số có cực đại, cực tiểu nằm về hai phía so với trục tung
A. m ∈ (1; 2)
B. m ∈ [1; 2]
C. m ∈ (- ∞; 1) ∪ (2; +∞)
D. m ∈ (- ∞; 1] ∪ [2; +∞)
Trả lời:
Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm trái dấu.
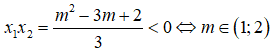
Chọn A
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm m để có hai điểm cực trị tại thỏa mãn
Xem lời giải »
Câu 2:
Tìm m để hàm số luôn đồng biến trên từng khoảng xác định của nó
Xem lời giải »
Câu 3:
Tìm m để phương trình có 6 nghiệm phân biệt
Xem lời giải »
Câu 4:
Tìm m để hàm số nghịch biến trên khoảng (1; 4)
Xem lời giải »
Câu 5:
Đồ thị hàm số có đường tiệm cận ngang có phương trình là
Xem lời giải »
Câu 6:
Hệ số góc của tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị hàm số với trục tung bằng
Xem lời giải »
Câu 7:
Cho đồ thị hàm số Gọi là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016. Khi đó bằng:
Xem lời giải »