Tìm số thực x; y để hai số phức z1 = 9y^2 – 4 – 10xi^5 và z2 = 8y^2 + 20i^11 là liên hợp của nhau?
Câu hỏi:
Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Trả lời:
Chọn D.
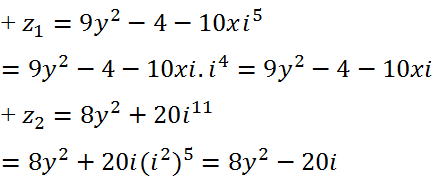
+ z1 và z2 là liên hợp của nhau khi và chỉ khi:
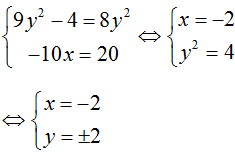
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm số phức z thỏa mãn hệ thức và
Xem lời giải »
Câu 2:
Cho số phức z thỏa mãn z2 - 6z + 13 = 0 . Giá trị của là:
Xem lời giải »
Câu 3:
Cho số phức z thỏa . Viết z dưới dạng z = a + bi. Khi đó tổng a + b có giá trị bằng bao nhiêu?
Xem lời giải »
Câu 4:
Có bao nhiêu số phức z thỏa mãn: và
Xem lời giải »

