Tìm tập hợp tất cả các giá trị của tham số m để phương trình log 2 x-log 2 (x-2)=m

❮ Bài trước Bài sau ❯

Câu hỏi:

Tìm tập hợp tất cả các giá trị của tham số m để phương trình $\log_{2} x - \log_{2} (x - 2) = m$ có nghiệm

A. $1 \leq m < + \infty$

B. $1 < m < + \infty$

C. $0 \leq m < + \infty$

D. $0 < m < + \infty$

Trả lời:

Phương trình đã cho tương đương với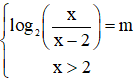

Để phương trình đã cho có nghiệm thì đường thẳng y = m cắt đồ thị hàm số $y = \log_{2} f (x)$ với $f (x) = \frac{x}{x - 2}$ trên khoảng $(2; + \infty)$

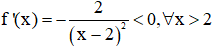Có và 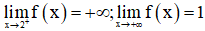nên ta có các tập giá trị của các hàm số là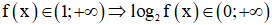

Vậy $0 < m < + \infty$

Đáp án cần chọn là: D.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Biết rằng phương trình $\log_{3} (3^{x + 1} - 1) = 2 x + \log_{\frac{1}{3}} 2$ có hai nghiệm $x_{1}$ và $x_{2}$ . Hãy tính tổng $S = 27^{x_{1}} + 27^{x_{2}}$

Xem lời giải »

Câu 2:

Tìm m để phương trình $4^{x} - 2^{x + 3} + 3 = m$ có đúng 2 nghiệm $x \in (1; 3)$

Xem lời giải »

Câu 3:

Tìm giá trị của tham số m để phương trình $9^{x} - m . 3^{x + 2} + 9 m = 0$ có hai nghiệm phân biệt $x_{1}; x_{2}$ thỏa mãn $x_{1} + x_{2} = 3$

Xem lời giải »

Câu 4:

Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có 2 nghiệm phân biệt $9^{1 - x} + 2 (m - 1) 3^{1 - x} + 1 = 0$

Xem lời giải »

Câu 5:

Giá trị nguyên nhỏ nhất của tham số m để phương trình $\log_{3} x - \log_{3} (x - 2) = m$ có nghiệm là

Xem lời giải »

Câu 6:

Tổng tất cả các nghiệm của phương trình $\log_{3} (7 - 3^{x}) = 2 - x$ bằng:

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Tìm tập hợp tất cả các giá trị của tham số m để phương trình log 2 x-log 2 (x-2)=m

Xem thêm bài tập Toán có lời giải hay khác: