Trong không gian Oxyz, cho đường thẳng d: x-1 / 1= y -2 / 2 = z- 3 / 1
Câu hỏi:
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (α): x + y -z – 2 = 0. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng (α), đồng thời vuông góc và cắt đường thẳng d?
Trả lời:
Chọn C
Phương trình tham số của đường thẳng 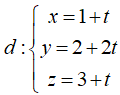
Lấy I ∈ d => I (1 + t; 2 + 2t; 3+ t), I ∈ (α) => 1 + t + 2 + 2t – (3 + t) - 2 = 0 ó t = 1 => I (2; 4; 4)
Vectơ chỉ phương của d là 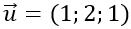
Vectơ chỉ pháp tuyến của (α) là 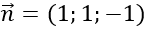
Ta có 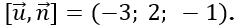
Đường thẳng cần tìm qua điểm I (2; 4; 4), nhận một VTCP có tọa độ là (-3; 2; -1) nên có
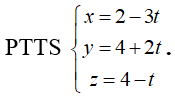
Kiểm tra A (5; 2; 5) ∈ Δ3 (với t = -1) , thấy A (5; 2; 5) thỏa mãn phương trình (*)
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho mặt phẳng (α): 2x + y -2z – 2 = 0, đường thẳng và điểm . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng Δ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng.
Xem lời giải »
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD (tham khảo hình vẽ bên).
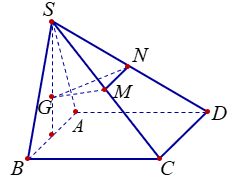
Tính côsin của góc giữa hai mặt phẳng (GMN) và (ABCD)
Xem lời giải »
Câu 3:
Trong không gian Oxyz, cho mặt phẳng x – z – 3 = 0 và điểm M (1; 1; 1). Gọi A là điểm thuộc tia Oz. Gọi B là hình chiếu của A lên (α). Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB bằng:
Xem lời giải »
Câu 4:
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục Oz sao cho MA2 + MB2 đạt giá trị nhỏ nhất.
Xem lời giải »


