Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23)
Câu hỏi:
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + ()2 + (z - 7)2 = 72. Mặt phẳng (P): x + by + cz + d = 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là
A. b + c + d = 2
B. b + c + d = 4
C. b + c + d = 3
D. b + c + d = 1
Trả lời:
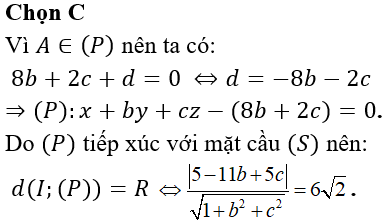
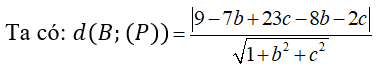
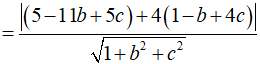
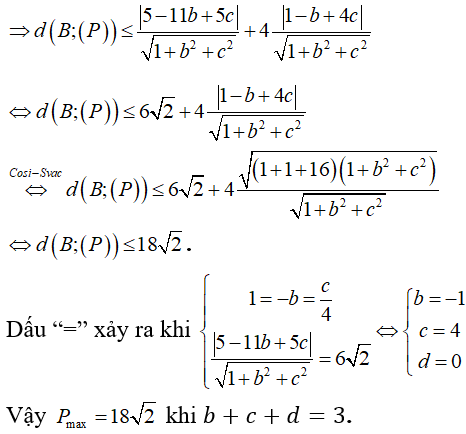
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 = 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng:
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; -1; 3). Tìm điểm M trên mặt phẳng (Oxy) sao cho lớn nhất.
Xem lời giải »
Câu 3:
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh bên bằng cạnh đáy. Đường thẳng MN (M ∈ A'C, N ∈ BC') là đường vuông góc chung của A'C và BC'. Tỷ số NB/NC' bằng:
Xem lời giải »
Câu 4:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x + y -2z + m = 0 và mặt cầu (S): x2 + y2 + z2 - 2x + 4y -6z - 2= 0. Có bao nhiêu giá trị nguyên của m để mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
Xem lời giải »
Câu 5:
Trong không gian với hệ trục Oxyz, cho hai điểm M (1; 2; 1); N (-1; 0; -1). Có bao nhiêu mặt phẳng (P) qua M, N cắt trục Ox, trục Oy lần lượt tại A, B (A ≠ B) sao cho AM = √3BN
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB = 2/3. Khi đó độ dài OM lớn nhất bằng:
Xem lời giải »
Câu 7:
Trong không gian Oxyz, cho đường thẳng và điểm A(3;2;0). Điểm đối xứng của điểm A qua đường thẳng d có tọa độ là:
Xem lời giải »
Câu 8:
Trong không gian Oxyz cho ba điểm A (1; 2; 3), B (1; 0; -1), C (2; -1; 2). Điểm D thuộc tia Oz sao cho độ dài đường cao xuất phát từ đỉnh D của tứ diện ABCD bằng có tọa độ là:
Xem lời giải »

