Trong không gian Oxyz, cho mặt cầu (S) có phương trình x^2+y^2+z^2-4x+2y-2z-3=0

Câu hỏi:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 4 x + 2 y - 2 z - 3 = 0$ và điểm $A (5; 3; - 2)$ . Một đường thẳng d thay đổi luôn đi qua A và luôn cắt mặt cầu tại hai điểm phân biệt $M, N$ .

Tính giá trị nhỏ nhất của biểu thức $S = A M + 4 A N$ .

A. $S_{\min} = 30$ .

$S_{\min} = 20$ .

$S_{\min} = 5 \sqrt{34} - 9$ .

$S_{\min} = \sqrt{34} - 3$ .

Trả lời:

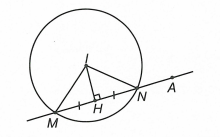
Media VietJack

Mặt cầu $(S)$ có tâm $I (2; - 1; 1)$ , bán kính $R = \sqrt{2^{2} + {(- 1)}^{2} + 1^{2} - (- 3)} = 3$ .

Ta có: $A I = \sqrt{{(2 - 5)}^{2} + {(- 1 - 3)}^{2} + {(1 + 2)}^{2}} = \sqrt{34} > R$ nên A nằm ngoài mặt cầu $(S)$ .

Ta lại có: $S = A M + 4 A N$ .

Đặt $A M = x, x \in [\sqrt{34} - 3; \sqrt{34} + 3]$ .

Mà $A M . A N = A I^{2} - R^{2} = 34 - 9 = 25 \Rightarrow A N = \frac{25}{A M}$ .

Do đó: $S = f (x) = x + \frac{100}{x}$ với $x \in [\sqrt{34} - 3; \sqrt{34} + 3]$ .

Ta có: $f^{'} (x) = 1 - \frac{100}{x^{2}} = \frac{x^{2} - 100}{x} < 0$ với $x \in [\sqrt{34} - 3; \sqrt{34} + 3]$ .

Do đó: $\min_{[\sqrt{34} - 3; \sqrt{34} + 3]} f (x) = f (\sqrt{34} + 3) = 5 \sqrt{34} - 9$ .

Dấu “=” xảy ra $\Leftrightarrow A, M, N, I$ thẳng hàng và $A M = \sqrt{34} + 3; A N = \sqrt{34} - 3$ .

Chọn C.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(-2,-2,1), A(1,2,-3) và đường thẳng $d : \frac{x + 1}{2} = \frac{y - 5}{2} = \frac{z}{- 1}$ .Tìm một vectơ chỉ phương $\vec{u}$ của đường thẳng D đi qua , vuông góc với đường thẳng đồng thời cách điểm một khoảng bé nhất.

Xem lời giải »

Câu 2:

Trong không gian Oxyz, cho hai điểm A(9,6,11), B(5,7,2) và điểm M di động trên mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 36$ .

Giá trị nhỏ nhất của $A M + 2 M B$ bằng

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2,-2,4), B(-3,3,-1) và đường thẳng

$d : \frac{x - 5}{2} = \frac{y - 2}{- 1} = \frac{z}{- 1}$ . Xét M là điểm thay đổi thuộc d, giá trị nhỏ nhất của

$2 M A^{2} + 3 M B^{2}$ bằng

Xem lời giải »

Câu 4:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1,0,3), B(-3,1,3), C(1,5,1). Gọi $M (x_{0}; y_{0}; z_{0})$ thuộc mặt phẳng tọa độ $(O x y)$ sao cho biểu thức $T = 2 |\vec{M A}| + |\vec{M B} + \vec{M C}|$ có giá trị nhỏ nhất. Giá trị của $x_{0} - y_{0}$ bằng

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1,2,-3),B(-2,-2,1) và mặt phẳng $(α)$ có phương trình $2 x + 2 y - z + 9 = 0$ . Gọi M là điểm thay đổi trên mặt phẳng $(α)$ sao cho M luôn nhìn đoạn AB dưới một góc vuông. Xác định phương trình đường thẳng MB khi MB đạt giá trị lớn nhất.

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Trong không gian Oxyz, cho mặt cầu (S) có phương trình x^2+y^2+z^2-4x+2y-2z-3=0

Xem thêm bài tập Toán có lời giải hay khác: