Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6) và ba điểm B, C, D
Câu hỏi:
Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6) và ba điểm B, C, D cùng thuộc mặt phẳng (Oyz). Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Lập phương trình mặt phẳng (MNP)
A. x + 1 = 0
B. x - 1 = 0
C. y + z - 1 = 0
D. x = 1 + t, y = -2, z = 3
Trả lời:
Đáp án B
* Tam giác ABC có MN là đường trung bình nên MN // BC (1)
Tam giác ACD có NP là đường trung bình nên NP // CD (2)
Từ (1) và (2) suy ra: (MNP) song song mp( BCD) hay (MNP) song song mp(Oyz).
* Mà mặt phẳng (Oyz) có 1 vecto pháp tuyến là (1; 0; 0) nên mặt phẳng (MNP) có VTPT (1; 0; 0).
* Điểm O(0; 0; 0). Gọi I(1; -2; 3) là trung điểm của AO. Suy ra; điểm I thuộc mặt phẳng (MNP).
* Phương trình mặt phẳng (MNP) là:
1(x- 1) + 0(y+ 2) + 0( z- 3) =0 hay x- 1= 0
Chọn B.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Một hình chóp có 40 cạnh. Hình chóp đó có bao nhiêu mặt?
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) lần lượt có phương trình là: 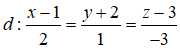
(P): 2x + y - 3z - 4 = 0. Trong những khẳng định dưới đây, khẳng định nào đúng?
Xem lời giải »
Câu 6:
Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6), B(1;1;1), C(0;3;0), D(0;0;3). Viết phương trình tham số của đường thẳng d chứa đường cao AH của tứ diện ABCD
Xem lời giải »
Câu 7:
Trong không gian Oxyz, cho hai đường thẳng cắt nhau: : x = 1 + t, y = 1, z = 1 - t, : x = -t, y = 2 + t, z = 1. Viết phương trình của mặt phẳng (P) chứa hai đường thẳng ,
Xem lời giải »
Câu 8:
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y - 3z + 1 = 0; 4x - 2y + ( + n)z - n = 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau
Xem lời giải »

