Trong không gian Oxyz, cho tứ diện S.ABC có S(0;0;1), A(1;0;1), B(0;1;1), C (0;0;2)
Câu hỏi:
Trong không gian Oxyz, cho tứ diện S.ABC có S(0;0;1), A(1;0;1), B(0;1;1), C (0;0;2). Hỏi tứ diện S.ABC có bao nhiêu mặt phẳng đối xứng?
A. 6
B. 1
C. 0
D. 3
Trả lời:
Chọn D
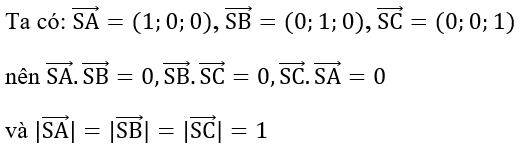
Tức là tứ diện SABC có các cạnh SA, SB, SC bằng nhau và đôi một vuông góc.
Vậy tứ diện SABC có tất cả ba mặt phẳng đối xứng đó là:
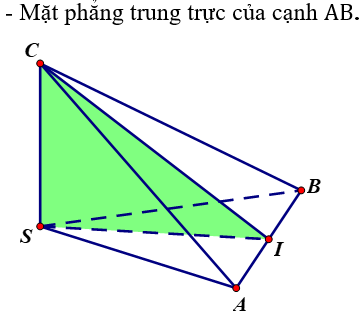
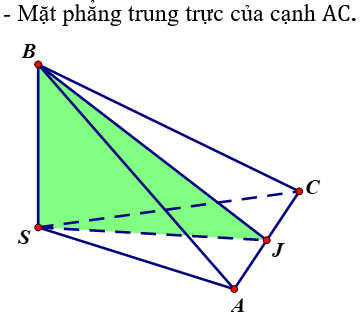
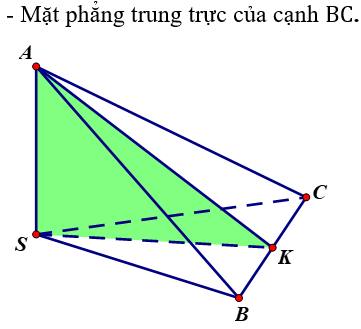
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho ba điểm A(0;0;-1), B(-1;1;0), C(1;0;1). Tìm điểm M sao cho 3MA2 + 2MB2 - MC2 đạt giá trị nhỏ nhất.
Xem lời giải »
Câu 3:
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
Xem lời giải »
Câu 4:
Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
Xem lời giải »
Câu 5:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là: .
Cho ba điểm A, M, B nằm trên mặt cầu (S) sao cho góc AMB = . Diện tích tam giác AMB có giá trị lớn nhất bằng?
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(2;1;3), B(1;-1;2), C(3;-6;1). Điểm M(x;y;z) thuộc mặt phẳng (Oyz) sao cho MA2 + MB2 + MC2 đạt giá trị nhỏ nhất. Tính giá trị của biểu thức P = x+y+z
Xem lời giải »
Câu 7:
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
Xem lời giải »
Câu 8:
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD', điểm N thuộc đoạn BD sao cho AM = DN = x, (0 < x < a√2/2). Tìm x theo a để đoạn MN ngắn nhất.
Xem lời giải »

