Trong không gian Oxyz, mặt cầu (S) tâm I (2; 5; 3) cắt đường thẳng d: x-1 / 2 = y / 1 =z -2 / 2
Câu hỏi:
Trong không gian Oxyz, mặt cầu (S) tâm I (2; 5; 3) cắt đường thẳng 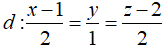 tại hai điểm phân biệt A, B với chu vi tam giác IAB bằng 10 + . Phương trình nào sau đây là phương trình của mặt cầu (S)?
tại hai điểm phân biệt A, B với chu vi tam giác IAB bằng 10 + . Phương trình nào sau đây là phương trình của mặt cầu (S)?
A. (x - 2)² + (y - 5)² + (z - 3)² = 100.
B. (x - 2)² + (y - 5)² + (z - 2)² = 7.
C. (x - 2)² + (y - 5)² + (z - 3)² = 25.
D. (x - 2)² + (y - 5)² + (z - 3)² = 28.
Trả lời:
Chọn C
Gọi R là bán kính của mặt cầu, H là trung điểm của AB.
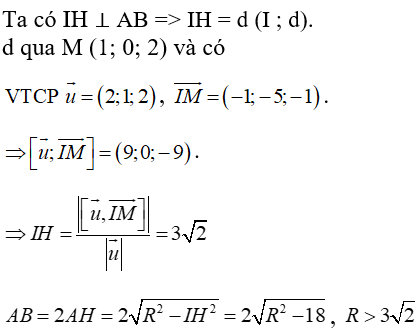
Chu vi tam giác IAB là
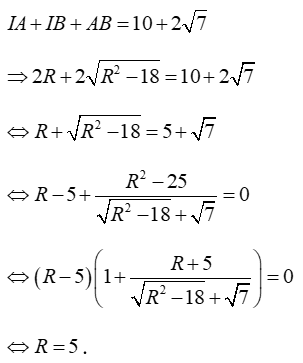
Mặt cầu (S) có tâm I (2; 5; 3), bán kính R = 5.
Phương trình mặt cầu (S) là: 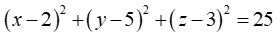
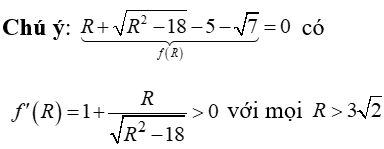
nên phương trình có nghiệm duy nhất R=5.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho (P): x - 2y + 2z - 5 = 0, A (-3;0;1), B (1;-1;3). Viết phương trình đường thẳng d đi qua A, song song với (P) sao cho khoảng cách từ B đến d là lớn nhất.
Xem lời giải »
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và . Trên đường thẳng d₁ lấy hai điểm A, B thỏa mãn AB=3. Trên đường thẳng d₂ lấy hai điểm C, D thỏa mãn CD=4. Tính thể tích V của tứ diện ABCD.
Xem lời giải »
Câu 3:
Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại A, góc ABC = , BC = 2a. Gọi D là điểm thỏa mãn . Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn BC sao cho BC = 4BH. Biết SA tạo với đáy một góc 600. Góc giữa hai đường thẳng AD và SC bằng:
Xem lời giải »
Câu 4:
Trong không gian Oxyz, cho điểm M (1;1;2). Mặt phẳng (P) qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất. Gọi 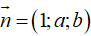 là một véc tơ pháp tuyến của (P). Tính S = a³ - 2b.
là một véc tơ pháp tuyến của (P). Tính S = a³ - 2b.
Xem lời giải »
![]() tại hai điểm phân biệt A, B với chu vi tam giác IAB bằng 10 + . Phương trình nào sau đây là phương trình của mặt cầu (S)?
tại hai điểm phân biệt A, B với chu vi tam giác IAB bằng 10 + . Phương trình nào sau đây là phương trình của mặt cầu (S)?
