Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + z -1 = 0
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + z -1 = 0 và điểm A (0; -2; 3), B (2; 0; 1). Điểm M (a; b; c) thuộc (P) sao cho MA + MB nhỏ nhất.
Giá trị của a2 + b2 + c2 bằng:
A. 41/4
B. 9/4
C. 7/4
D. 3
Trả lời:
Chọn B
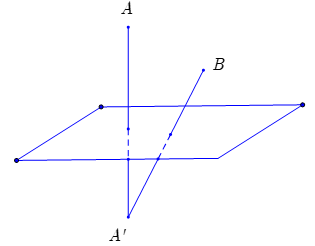
Ta có A, B cùng nằm về một phía của (P). Gọi A' đối xứng với A qua (P) suy ra A' (-2; 2; 1). Ta có MA + MB = MA' + MB ≥ BA'. Dấu bằng xảy ra khi M là giao điểm của BA' và (P). Xác định được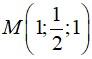 
. Suy ra Chọn B
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho hai điểm M(0;1;3), N(10;6;0) và mặt phẳng (P): x - 2y + 2z -10 = 0. Điểm I(-10; a; b) thuộc mặt phẳng (P) sao cho |IM - IN| lớn nhất. Khi đó tổng T = a + b bằng:
Xem lời giải »
Câu 2:
Trong không gian tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 và mặt phẳng (P): x + 2y - 2z - 2 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính là:
Xem lời giải »
Câu 3:
Trong không gian tọa độ Oxyz cho mặt cầu (S): x2 + y2 + z2 + 4x - 6y + m = 0 và đường thẳng Δ là giao tuyến của hai mặt phẳng (α): x + 2y - 2z - 4 = 0 và (β): 2x - 2y - z + 1 = 0. Đường thẳng Δ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn AB = 8 khi:
Xem lời giải »
Câu 4:
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông cân tại A, cạnh BC = a√6. Góc giữa mặt phẳng (AB'C) và mặt phẳng (BCC'B') bằng 600. Tính thể tích V của khối lăng trụ ABC.A'B'C'?
Xem lời giải »
