Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm , có tâm thuộc mặt phẳng , đồng thời có bán kính nhỏ nhất, hãy tính bán kính R của mặt cầu (S)?
A. 1
B.
C. 2
D.
Trả lời:
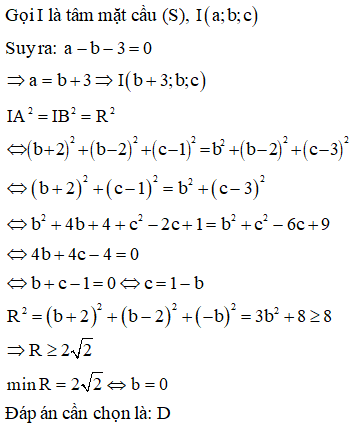
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và 2 mặt phẳng (P) và (Q) lần lượt có phương trình . Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng d, tiếp xúc với hai mặt phẳng (P) và (Q)
Xem lời giải »
Câu 2:
Trong khôn gian Oxyz, cho biết có hai mặt cầu có tâm nằm trên đường thẳng , tiếp xúc đồng thời với hai mặt phẳng và . Gọi là bán kính của hai mặt cầu đó. Tỉ số bằng:
Xem lời giải »
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và hai mặt phẳng . Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiêp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S)
Xem lời giải »
Câu 4:
Trong không gian Oxyz, cho 3 điểm A(0;1;1), B(3;0;-1) và C(0;21;-19) mặt cầu . Điểm M thuộc mặt cầu (S) sao cho tổng đạt giá trị nhỏ nhất, khi đó, độ dài vec tơ là:
Xem lời giải »

