Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và hai mặt phẳng . Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiêp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S)
A.
B.
C.
D.
Trả lời:
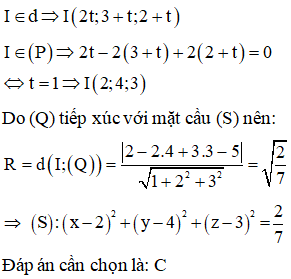
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và 2 mặt phẳng (P) và (Q) lần lượt có phương trình . Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng d, tiếp xúc với hai mặt phẳng (P) và (Q)
Xem lời giải »
Câu 2:
Trong khôn gian Oxyz, cho biết có hai mặt cầu có tâm nằm trên đường thẳng , tiếp xúc đồng thời với hai mặt phẳng và . Gọi là bán kính của hai mặt cầu đó. Tỉ số bằng:
Xem lời giải »
Câu 3:
Trong không gian Oxyz, cho 3 điểm A(0;1;1), B(3;0;-1) và C(0;21;-19) mặt cầu . Điểm M thuộc mặt cầu (S) sao cho tổng đạt giá trị nhỏ nhất, khi đó, độ dài vec tơ là:
Xem lời giải »
Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-y-2z+1=0 và ba điểm . Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB. AC, BC?
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho 3 điểm A(6;0;0), B(0;6;0), C(0;0;6). Hai mặt cầu có phương trình và cắt nhau theo đường tròn (C). Hỏi có bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa (C) và tiếp xúc với ba đường thẳng AB, BC, CA?
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.
Xem lời giải »

