Tứ diện ABCD có AB=2, CD+2 căn 2, góc ABC=góc DAB=90độ và góc giữa AD, BC bằng 45 độ
Câu hỏi:
Tứ diện ABCD có AB=2,CD=2√2 ^ABC=^DAB=90° và góc giữa AD, BC bằng 45°. Khi đó, bán kính mặt cầu ngoại tiếp tứ diện là:
A. √2
B. √3
C. 2√3
D. √5
Trả lời:
Dựng hình chữ nhật ABED. Ta có mặt cầu tâm I ngoại tiếp tứ diện ABCD cũng phải đi qua điểm E.
Do đó I là tâm mặt cầu ngoại tiếp tứ diện BCDE.
Ta có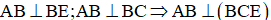 
Vì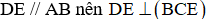 
Dựng tam giác vuông cân COE trong mặt phẳng (BCE) sao cho B và O nằm cùng phía với CE
Ta chứng minh được O là tâm đường tròn ngoại tiếp ∆BCE. Dựng hình chữ nhật MEOI với M là trung điểm DE thì I là giao điểm của mặt phẳng trung trực của DE với trục của đường tròn ngoại tiếp ∆BCE nên I là tâm mặt cầu ngoại tiếp tứ diện BCDE.
Ta có:
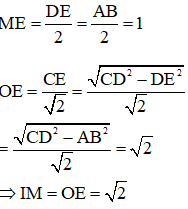
(vì tam giác CED vuông tại E)
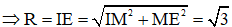
Đáp án cần chọn là: B
