100 Bài tập Giá trị lớn nhất, nhỏ nhất của hàm số có lời giải (cơ bản) - Toán lớp 12

---

100 Bài tập Giá trị lớn nhất, nhỏ nhất của hàm số có lời giải (cơ bản)

Link tải 100 Bài tập Giá trị lớn nhất, nhỏ nhất của hàm số có lời giải (cơ bản)

Với 100 Bài tập Giá trị lớn nhất, nhỏ nhất của hàm số có lời giải (cơ bản) Toán lớp 12 tổng hợp 100 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giá trị lớn nhất, nhỏ nhất của hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1. Giá trị nhỏ nhất của hàm số y = x³ – 3x+ 5 trên đoạn [0; 2] là:

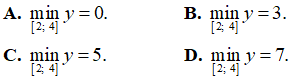
Lời giải:

Đáp án: B

Nhận xét: Hàm số f(x) liên tục trên [0;2]

Ta có y' = 3x² - 3 = 3(x² - 1);

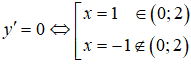
y(1) = 3; y(0) = 5; y(2) = 7.

Do đó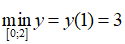

Bài 2. Giá trị nhỏ nhất của hàm số f(x) = x³ – 3x² – 9x + 35 trên đoạn [-4; 4] là:

Lời giải:

Đáp án: C

Nhận xét: Hàm số f(x) liên tục trên [-4; 4]

Ta có f'(x) = 3x² - 6x - 9;

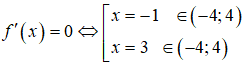
f(-4) = -41; f(-1) = 40; f(3) = 8; f(4) = 15.

Do đó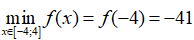

Bài 3. Giá trị lớn nhất của hàm số f(x) = x³ – 8x² + 16x – 9 trên đoạn [1; 3] là:

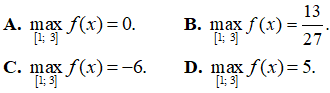
Lời giải:

Đáp án: B

Nhận xét: Hàm số f(x) liên tục trên [1;3]

Ta có f'(x) = 3x² - 16x + 16;

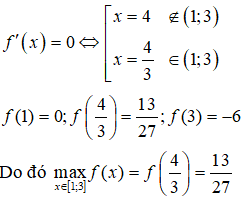
Bài 4. Giá trị lớn nhất của hàm số f(x)= x⁴ – 2x² + 1 trên đoạn [0; 2] là:

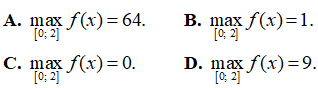
Lời giải:

Đáp án: D

Nhận xét: Hàm số f(x) liên tục trên [0;2]

Ta có f'(x) = 4x³ - 4x = 4x(x² - 1)

Xét trên (0; 2) . Ta có f'(x) = 0 ⇔ x = 1; Khi đó f(1) = 0; f(0) = 1; f(2) = 9

Do đó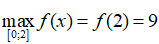

Bài 5. Giá trị nhỏ nhất của hàm số y= x. (x+ 2). (x+ 4). (x+ 6) + 5 trên nữa khoảng [-4; +∞] là:

Lời giải:

Đáp án: B

Nhận xét: Hàm số f(x) liên tục trên [-4; +∞]

Ta có: y = (x² + 6x)(x² + 6x + 8) + 5. Đặt t = x² + 6x. Khi đó y = t2 + 8t + 5

Xét hàm số g(x) = x² + 6x với x ≥ -4. Ta có g'(x) = 2x + 6; g'(x) = 0⇔ x = -3

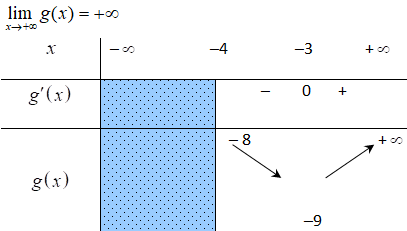
Suy ra t ∈ [-9; +∞]

Yêu cầu bài toán trở thành tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = h(t) = t2 + 8t + 5 với t ∈ [-9; +∞]. Ta có h'(t) = 2t + 8; h'(t) = 0 ⇔ t = -4;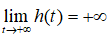

Bảng biến thiên

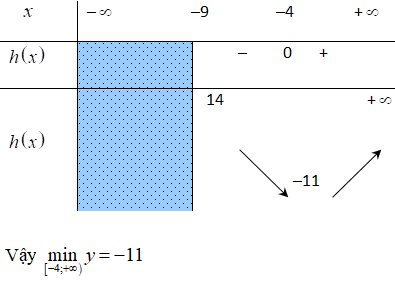
Bài 6. Giá trị nhỏ nhất của hàm số 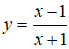trên đoạn [0; 3] là:

Lời giải:

Đáp án: C

Nhận xét: Hàm số đã cho liên tục trên [0;3]

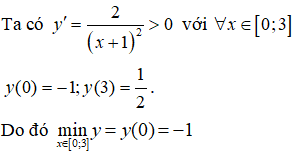
Bài 7. Giá trị nhỏ nhất của hàm số 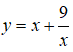trên đoạn [2; 4] là:

Lời giải:

Đáp án: A

Nhận xét: Hàm số đã cho liên tục trên [2;4]

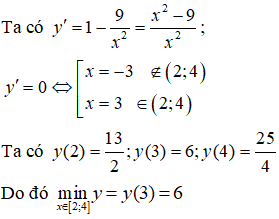
Bài 8. Giá trị nhỏ nhất của hàm số 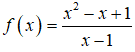trên khoảng (1;+∞) là:

Lời giải:

Đáp án: B

Hàm số xác định ∀ x ∈ (1;+∞)

Nhận xét: Hàm số f(x) liên tục trên

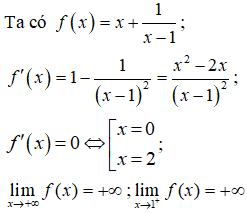
Bảng biến thiên

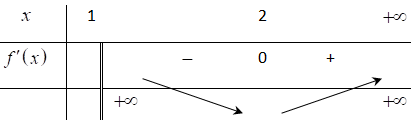
Từ bảng biến thiên ta có: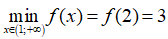

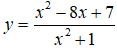
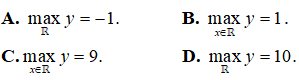
Bài 9. Giá trị lớn nhất của hàm số là:

Lời giải:

Đáp án: C

Hàm số xác định ∀ x ∈ R

Nhận xét: Hàm số f(x) liên tục trên R

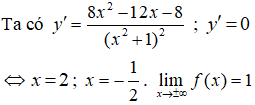
Bảng biến thiên

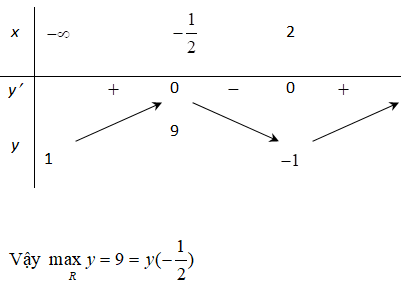
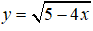
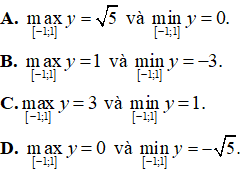
Bài 10. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-1; 1] là:

Lời giải:

Đáp án: C

Điều kiện xác định: 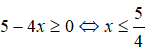. Suy ra hàm số xác định ∀ x ∈ [-1; 1]

Nhận xét: Hàm số f(x) liên tục trên đoạn [-1; 1]

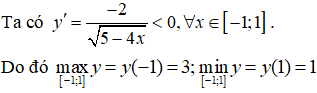
Bài 11. Giá trị lớn nhất của hàm số 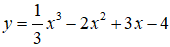trên đoạn [1; 5] là:

Lời giải:

Đáp án: A

TXĐ: D = R. Ta có: y' = x² -4x + 3; y' = 0 ⇔ x² - 4x + 3 = 0 ⇔ x = 1 hoặc x = 3.

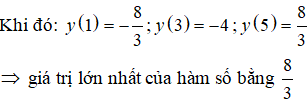
Bài 12. Giá trị lớn nhất của hàm số 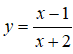trên đoạn [0; 2] là:

Lời giải:

Đáp án: A

TXĐ: D = R\{-2}.

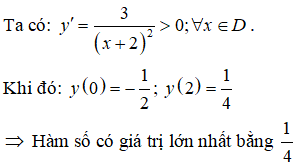
Bài 13. Cho hàm số 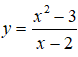. Khẳng định nào sau đây đúng về giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [3; 4]:

A. Hàm số có giá trị nhỏ nhất bằng 3/2.

B. Hàm số có giá trị lớn nhất bằng 2.

C. Hàm số có giá trị lớn nhất bằng 6.

D. Hàm số có giá trị lớn nhất bằng 13/2 và giá trị nhỏ nhất bằng 6.

Lời giải:

Đáp án: D

TXĐ: D = R \ 2.

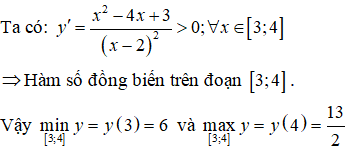
Bài 14. Hàm số y = x² +2x+ 1 có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0; 1] lần lượt là y₁; y₂. Khi đó tích y₁.y₂ bằng:

A. 5.     B. -1.     C. 4.     D. 1.

Lời giải:

Đáp án: C

TXĐ: D = R.

y' = 2x + 2; y' = 0 ⇔ 2x + 2 = 0 ⇔ x = -1 ∉ [0; 1]. y(0) = 1; y(1) = 4 suy ra y₁.y₂ = 4

Bài 15. Hàm số 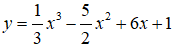đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [1; 3] tại điểm có hoành độ lần lượt là x₁ ; x₂. Khi đó tổng x₁ + x₂ bằng

A. 2.     B. 5.     C. 4.     D. 3.

Lời giải:

Đáp án: D

TXĐ: D = R. Ta có: y ' = x² - 5x + 6; y' = 0 ⇔ x² - 5x + 6 = 0 ⇔ x = 2 hoặc x = 3

Khi đó:

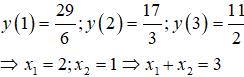
Bài 16. Hàm số 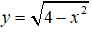đạt giá trị nhỏ nhất tại x. Giá trị của x là:

A. x = 3

B. x = 0 hoặc x = 2 .

C. x = 0

D. x = - 2 hoặc x = 2.

Lời giải:

Đáp án: D

TXĐ: D = [-2; 2].

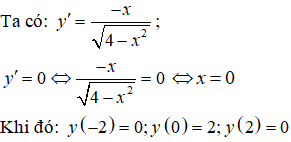
Hàm số đạt giá trị nhỏ nhất tại điểm có hoành độ x = ±2

Bài 17. Hàm số y = (x - 1)² + (x + 3)² có giá trị nhỏ nhất bằng:

A. 3.     B. -1.     C. 10.     D. 8.

Lời giải:

Đáp án: D

TXĐ: D = R. Ta có: y = (x - 1)² + (x + 3)² = 2x² + 4x + 10.

Ta có: y' = 4x + 4; y' = 0 ⇔ x = -1;

Bảng biến thiên:

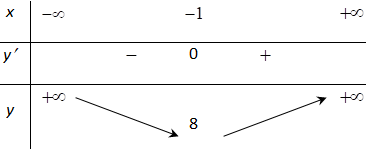
Từ BBT ta thấy hàm số có giá trị nhỏ nhất bằng 8 .

Bài 18. Giá trị nhỏ nhất của hàm số 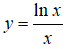trên đoạn [1; e] bằng là:

Lời giải:

Đáp án: A

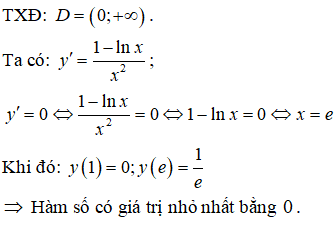
Bài 19. Hàm số 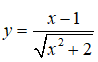đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [-3; 0] lần lượt tại x₁; x₂. Khi đó x₁.x₂ bằng:

A. 2.     B. 0.     C. 6.     D. √2.

Lời giải:

Đáp án: B

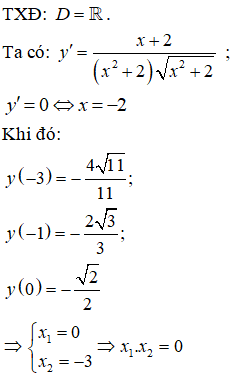
Bài 20. Hàm số 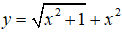có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1; 1] lần lượt là:

Lời giải:

Đáp án: B

TXĐ : D = R.

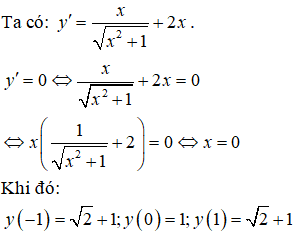
Bài 21. Giá trị lớn nhất của hàm số 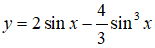trên [0; π] là:

Lời giải:

Đáp án: D

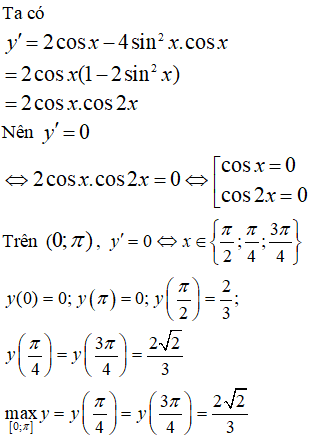
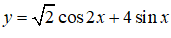
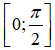
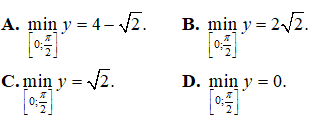
Bài 22. Giá trị nhỏ nhất của hàm số trên đoạn là:

Lời giải:

Đáp án: C

TXĐ: D = R. Ta có

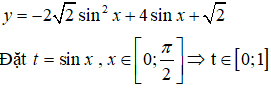
Khi đó, bài toán trở thành tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

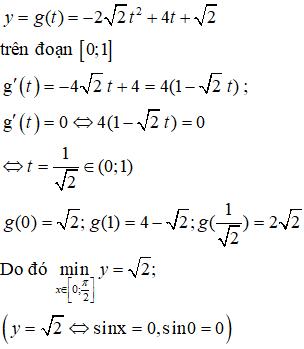
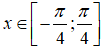
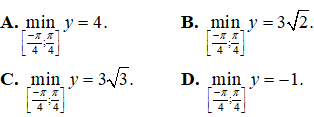
Bài 23. Giá trị nhỏ nhất của hàm số y = 5cosx - cos5x với là:

Lời giải:

Đáp án: A

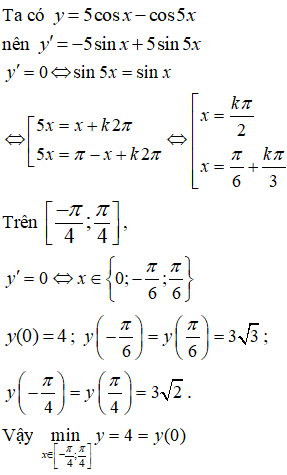
Bài 24. Hàm số y = sinx+ 1 đạt giá trị lớn nhất trên đoạn 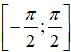bằng:

Lời giải:

Đáp án: A

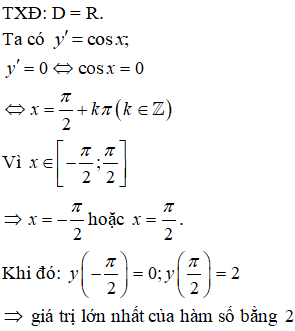
Bài 25. Hàm số y = cos2x - 3 đạt giá trị nhỏ nhất trên đoạn [0 ; π] bằng:

A. - 4     B. - 3     C.- 2     D. 0

Lời giải:

Đáp án: A

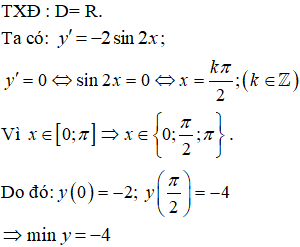
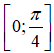
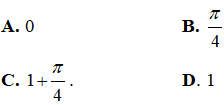
Bài 26. Hàm số y = tanx + x đạt giá trị nhỏ nhất trên đoạn tại điểm có hoành độ bằng:

Lời giải:

Đáp án: A

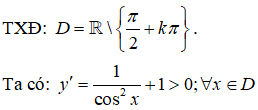
⇒ Hàm số đồng biến trên D ⇒ min y = 0.

Bài 27. Hàm số y= sinx+ cosx có giá trị nhỏ nhất, giá trị lớn nhất lần lượt là:

Lời giải:

Đáp án: B

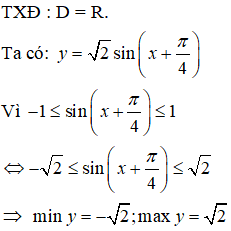
Bài 28. Hàm số y = 3sinx- 4sin³x có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:

A. 3;-4     B. 1; 0

C. 1; -1     D. 0; -1

Lời giải:

Đáp án: C

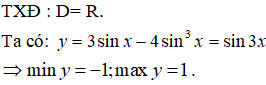
Bài 29. Hàm số y = sin²x + 2 có giá trị nhỏ nhất, giá trị lớn nhất lần lượt bằng:

A. 0; 2     B. 1; 3

C. 1; 2     D. 2; 3

Lời giải:

Đáp án: D

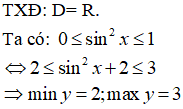
Bài 30. Hàm số y = - 9sinx – sin3x có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0; π] lần lượt là:

A. 8; 0     B. 0; - 8

C. 1; -1     D. 0; -1

Lời giải:

Đáp án: B

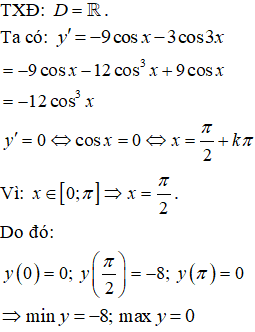
Bài 31. Hàm số 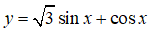có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:

Lời giải:

Đáp án: D

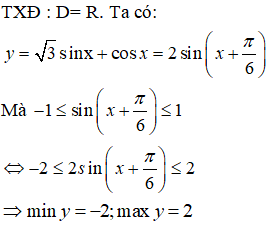
Bài 32. Hàm số y = cos²x - 2cosx - 1 có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn [0; π] lần lượt bằng y₁ ; y₂. Khi đó tích y₁. y₂ có giá trị bằng:

Lời giải:

Đáp án: B

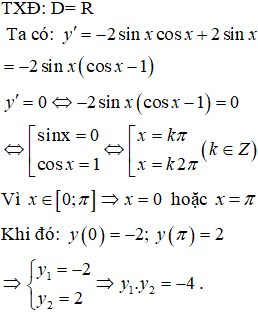
Bài 33. Hàm số y = cos2x + 2sinx có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 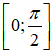lần lượt là y₁; y₂. Khi đó tích y₁. y₂ có giá trị bằng:

Lời giải:

Đáp án: A

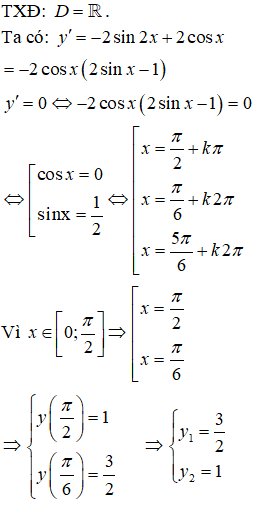
Bài 34. Hàm số y = cos2x – 4sinx + 4 có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn 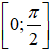là:

Lời giải:

Đáp án: C

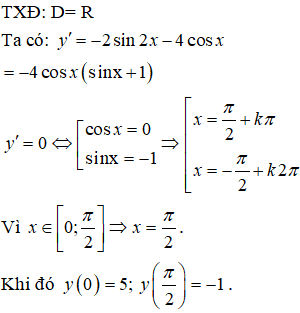
Bài 35. Hàm số y = tanx+ cotx đạt giá trị lớn nhất trên đoạn 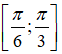tại điểm có hoành độ là:

Lời giải:

Đáp án: C

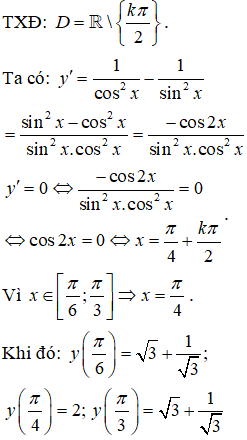
Bài 36. Hàm số y = cosx(sinx+ 1) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0; π] lần lượt là:

Lời giải:

Đáp án: C

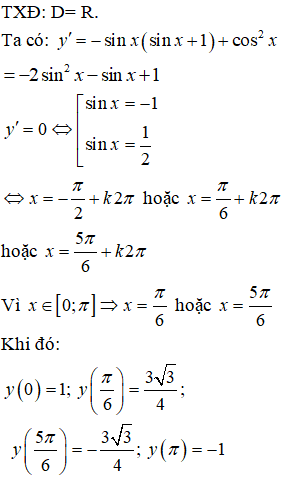
Bài 37. Hàm số y = sin³x+ cos³x có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0; π] lần lượt là y₁; y₂. Khi đó hiệu y₁ - y₂ có giá trị bằng:

A. 4     B. 1     C. 3     D. 2

Lời giải:

Đáp án: D

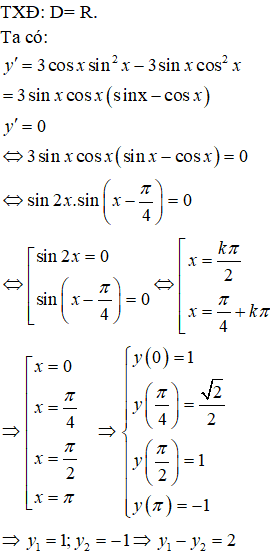
Bài 38. Giá trị nhỏ nhất của hàm số y = e^x(x² - x - 1) trên đoạn [0;2] là

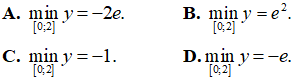
Lời giải:

Đáp án: D

Bài 39. Giá trị nhỏ nhất của hàm số y = e^x(x² - 3) trên đoạn [-2; 2]?

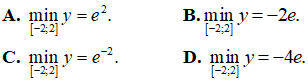
Lời giải:

Đáp án: B

Hàm số y = e^x(x² - 3) liên tục trên đoạn [-2 ; 2]

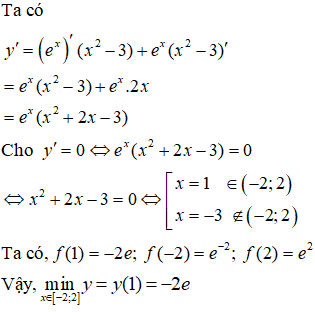
Bài 40. Giá trị lớn nhất của hàm số y = e^x + 4e^-x + 3x trên đoạn [1 ; 2] bằng

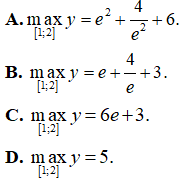
Lời giải:

Đáp án: A

Hàm số y = e^x + 4e^-x + 3x liên tục trên đoạn [1; 2]