120 Bài tập Tính đơn điệu của hàm số có lời giải (cơ bản) - Toán lớp 12

---

120 Bài tập Tính đơn điệu của hàm số có lời giải (cơ bản)

Link tải 120 Bài tập Tính đơn điệu của hàm số có lời giải (cơ bản)

Với 120 Bài tập Tính đơn điệu của hàm số có lời giải (cơ bản) Toán lớp 12 tổng hợp 120 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính đơn điệu của hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1. Tìm khoảng nghịch biến của hàm số y = x⁴ – 6x² + 8x+ 1.

Lời giải:

Đáp án: B

Hàm số đã cho xác định trên D = R.

Đạo hàm: y’ = 4x³ – 12x + 8.

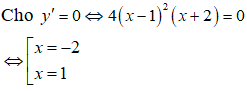
Bảng biến thiên :

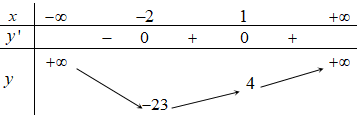
Dựa vào bảng biến thiên, hàm số nghịch biến trên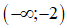

Bài 2. Tìm khoảng đồng biến của hàm số y= x⁴ + 4x+ 6.

Lời giải:

Đáp án: A

Tập xác định: D = R.

Tính: y’= 4x³ + 4. Cho y’= 0 khi 4x³ + 4 = 0 ⇔ x = -1

Bảng biến thiên:

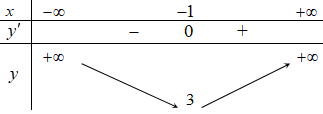
Dựa vào bảng biến thiên, hàm số đồng biến trên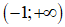

Bài 3. Cho hàm số f(x) có đạo hàm trên (a; b). Khẳng định nào sau đây là sai?

A. Nếu f’(x) > 0 ∀ x ∈ (a; b) thì hàm số f(x) đồng biến trên khoảng (a; b).

B. Hàm số f(x) nghịch biến trên khoảng (a; b) khi và chỉ khi 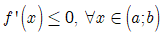và f’(x)= 0 chỉ tại một hữu hạn điểm x (a; b).

C. Nếu hàm số f(x) đồng biến trên khoảng (a; b) thì f’(x) > 0; ∀ x ∈ (a; b) .

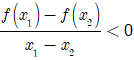
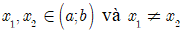
D. Hàm số f(x) nghịch biến trên khoảng (a; b) khi và chỉ khi với mọi

Lời giải:

Đáp án: C

Sửa lại cho đúng là Nếu hàm số f(x) đồng biến trên (a; b) thì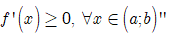

Bài 4. Khẳng định nào sau đây là đúng?

A. Nếu hàm số f(x) đồng biến trên (a; b) , hàm số g(x) nghịch biến trên (a;b) thì hàm số f(x) + g(x) đồng biến trên (a; b) .

B. Nếu hàm số f(x) đồng biến trên (a; b) , hàm số g(x) nghịch biến trên (a; b) và đều nhận giá trị dương trên (a; b) thì hàm số f(x) . g(x) đồng biến trên (a; b) .

C. Nếu các hàm số f(x); g(x) đồng biến trên (a; b) thì hàm số f(x).g(x) đồng biến trên (a; b).

D. Nếu các hàm số f(x); g(x) nghịch biến trên (a; b) và đều nhận giá trị âm trên (a; b) thì hàm số f(x). g(x) đồng biến trên (a; b) .

Lời giải:

Đáp án: D

A sai: Vì tổng của hàm đồng biến với hàm nghịch biến không kết luận được điều gì.

B sai: Để cho khẳng định đúng thì g(x) đồng biến trên (a; b) .

C sai: Hàm số f(x); g(x) phải là các hàm dương trên (a; b) mới thoả mãn.

D đúng.

Bài 5. Khẳng định nào sau đây là sai?

A. Nếu hàm số f(x) đồng biến trên (a;b) thì hàm số - f(x) nghịch biến trên (a; b).

B. Nếu hàm số f(x) đồng biến trên (a; b) thì hàm số 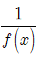nghịch biến trên (a; b).

C. Nếu hàm số f(x) đồng biến trên (a; b) thì hàm số f(x) + 10 đồng biến trên (a; b) .

D. Nếu hàm số f(x) đồng biến trên (a; b) thì hàm số - f(x) - 10 nghịch biến trên (a; b).

Lời giải:

Đáp án: B

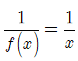
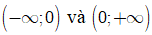
Ví dụ hàm số f(x) = x đồng biến trên R, trong khi đó hàm số nghịch biến trên . Do đó B sai.

Bài 6. Nếu hàm số y= f(x) đồng biến trên khoảng (-1; 2) thì hàm số y= f(x+2) đồng biến trên khoảng nào trong các khoảng sau đây?

A. (-1;2)     B. (1;4)     C. (-3; 0)     D. (-2; 4)

Lời giải:

Đáp án: C

Tịnh tiến đồ thị hàm số y= f(x) sang trái 2 đơn vị, ta sẽ được đồ thị của hàm số

y= f(x+ 2). Khi đó, do hàm số f(x) liên tục và đồng biến trên khoảng (-1; 2) nên hàm số y= f(x+ 2) đồng biến trên (- 3; 0).

Cách trắc nghiệm nhanh.

Ta có x + 2 ∈ (-1; 2) nên – 1 < x+2 < 2

Suy ra: - 3 < x < 0.

Bài 7. Nếu hàm số y= f(x) đồng biến trên khoảng (0; 2) thì hàm số y= f(2x) đồng biến trên khoảng nào?

A. (0; 2)     B. (0;4)     C. (0; 1)     D. (-2;0)

Lời giải:

Đáp án: C

Tổng quát: Hàm số y= f(x) liên tục và đồng biến trên khoảng (a; b) thì hàm số y= f(nx) liên tục và đồng biến trên khoảng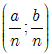

Cách trắc nghiệm nhanh.

Ta có : 2x ∈ (0; 2) nên 0 < 2x < 2

Suy ra: 0 < x < 1.

Bài 8. Cho hàm số 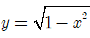. Khẳng định nào sau đây là đúng?

A. Hàm số đã cho đồng biến trên [0;1].

B. Hàm số đã cho đồng biến trên toàn tập xác định

C. Hàm số đã cho nghịch biến trên [0; 1].

D. Hàm số đã cho nghịch biến trên toàn tập xác định.

Lời giải:

Đáp án: C

Tập xác định D= [-1; 1].

Đạo hàm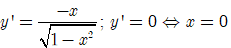

Bảng biến thiên:

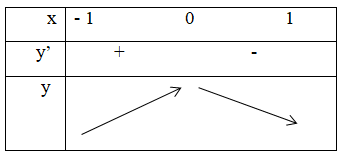
Suy ra được hàm số nghịch biến trên [0;1].

Bài 9. Hàm số 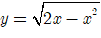nghịch biến trên khoảng nào đã cho dưới đây

A. (0; 2)     B. (0;1)     C. (1; 2)     D. (-1;1)

Lời giải:

Đáp án: C

Tập xác định D= [0; 2].

Đạo hàm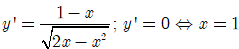

Bảng biến thiên:

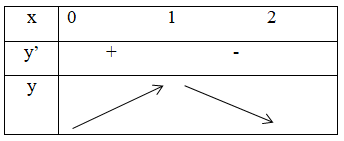
suy ra được hàm số nghịch biến trên khoảng (1; 2).

Bài 10. Cho hàm số 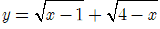. Mệnh đề nào sau đây là đúng?

A. Hàm số đã cho nghịch biến trên (1; 4).

B. Hàm số đã cho nghịch biến trên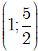

C. Hàm số đã cho nghịch biến trên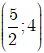

D. Hàm số đã cho nghịch biến trên R.

Lời giải:

Đáp án: C

Tập xác định: D= [1; 4].

Đạo hàm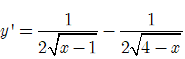

Xét phương trình

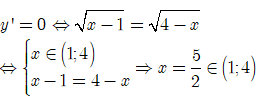
Bảng biến thiên:

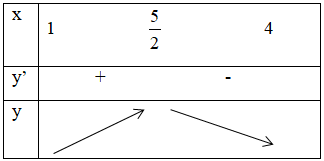
Dựa vào bảng biến thiên, suy ra được hàm số nghịch biến trên khoảng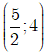

Bài 11. Hàm số nào sau đây đồng biến trên R?

Lời giải:

Đáp án: B

Xét phương án B. y = 2x – sin2x + 5

Nên đạo hàm: y’= 2 – 2cos2x = 2(1- cos2x) ≥ 0; ∀ x ∈ R

Và y’= 0 khi cos2x = 1.

Phương trình cos2x = 1 có vô số nghiệm nhưng các nghiệm tách rời nhau nên hàm số đồng biến trên R

Bài 12. Hàm số nào sau đây đồng biến trên R?

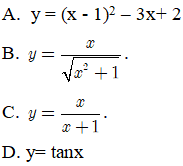
Lời giải:

Đáp án: B

Xét hàm số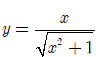

Hàm số có tập xác định D= R.

Ta có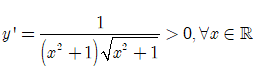

Suy ra hàm số đồng biến trên R.

Bài 13. Khẳng định nào sau đây là sai?

A. Hàm số y = 2x + cosx đồng biến trên R.

B. Hàm số y = - x³ – 3x +1 nghịch biến trên R.

C. Hàm số 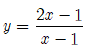đồng biến trên mỗi khoảng xác định.

D. Hàm số y = 2x⁴ + x² + 1 nghịch biến trên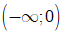

Lời giải:

Đáp án: C

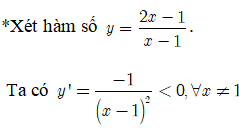
Suy ra hàm số nghịch biến trên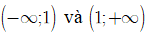

Bài 14. Cho hàm số y= f(x) liên tục trên R và có bảng biến thiên như sau:

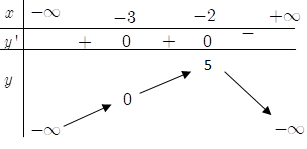
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?

I. Hàm số đã cho đồng biến trên các khoảng 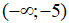và (-3; -2).

II. Hàm số đã cho đồng biến trên khoảng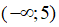

III. Hàm số đã cho nghịch biến trên khoảng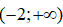

IV. Hàm số đã cho đồng biến trên khoảng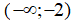

A. 1     B. 2     C. 3     D .4

Lời giải:

Đáp án: A

Nhìn vào bảng biến thiên ta thấy đồ thị hàm số đã cho đồng biến trên khoảng ; nghịch biến trên khoảng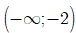

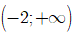
Suy ra II là sai; III: đúng và IV là đúng.

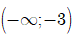
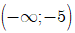
Ta thấy khoảng chứa khoảng nên I Đúng.

Vậy chỉ có II sai.

Bài 15. Cho hàm số y= f(x) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?

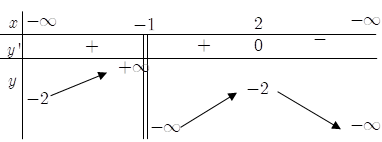
A. Hàm số đã cho đồng biến trên các khoảng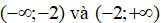

B. Hàm số đã cho đồng biến trên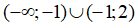

C. Hàm số đã cho đồng biến trên khoảng (0;2) .

D. Hàm số đã cho đồng biến trên(-2; 2).

Lời giải:

Đáp án: C

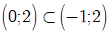
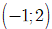
Vì , mà hàm số đồng biến trên khoảng nên suy ra C đúng.

Bài 16. Cho hàm số y= f(x) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?

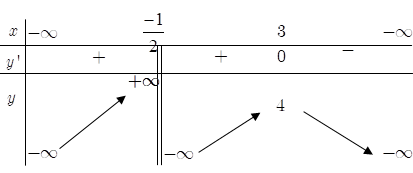
A. Hàm số đã cho đồng biến trên các khoảng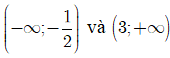

B. Hàm số đã cho đồng biến trên khoảng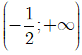

C. Hàm số đã cho nghịch biến trên khoảng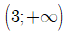

D. Hàm số đã cho đồng biến trên khoảng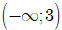

Lời giải:

Đáp án: C

Dựa vào bảng biến thiên ta thấy hàm số

● Đồng biến trên các khoảng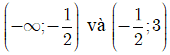

● Nghịch biến trên khoảng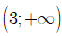

Bài 17. Tìm khoảng đồng biến của hàm số: y= - x³ + 6x² – 9x+ 4.

Lời giải:

Đáp án: B

Hàm số đã cho xác định trên D= R.

Tính y’= - 3x² + 12x – 9.

Cho y’= 0 hay – 3x² + 12x - 9 = 0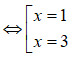

Bảng biến thiên:

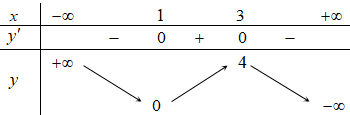
Dựa vào bảng biến thiên,hàm số đồng biến trên (1; 3).

Bài 18. Cho hàm số: y= f(x) = x³ + 3x² + 3x+ 2. Hãy chọn câu đúng :

A. Hàm số f(x) nghịch biến trên R.

B. Hàm số f(x) đồng biến trên R.

C. Hàm số f(x) không đổi trên R.

D. Hàm số f(x) nghịch biến trên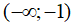

Lời giải:

Đáp án: B

Hàm số đã cho xác định trên D = R.

Tìm y’ = 3x² + 6x + 3.

Cho y’ = 0 hay 3x² + 6x + 3 = 0 ⇔ x = -1

Bảng biến thiên:

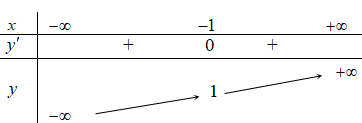
Dựa vào bảng biến thiên, hàm số đồng biến trên D= R.

Bài 19. Tìm khoảng đồng biến của hàm số: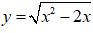

Lời giải:

Đáp án: B

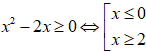
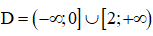
Hàm số đã cho xác định khi: nên tập xác định:

Ta có: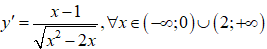

Hàm số không có đạo hàm tại: x = 0 ; x = 2.

Cho 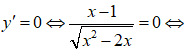x - 1 = 0 hay x = 1.

Bảng biến thiên:

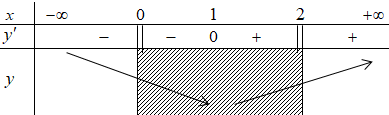
Dựa vào bảng biến thiên, hàm số đồng biến trên .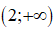

Bài 20. Tìm khoảng đồng biến của hàm số: .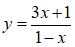

Lời giải:

Đáp án: C

Hàm số xác định và liên tục trên D = R\ {1}.

Tìm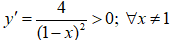

Bảng biến thiên:

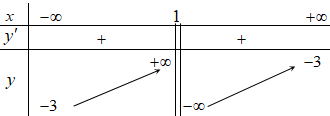
Hàm số đã cho đồng biến trên các khoảng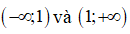

Bài 21. Tìm khoảng nghịch biến của hàm số: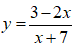

Lời giải:

Đáp án: C

Hàm số đã cho xác định và liên tục trên D = R\ {- 7}.

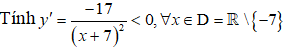
Bảng biến thiên:

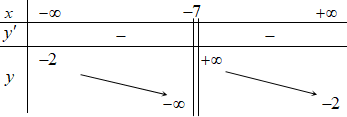
Hàm số đã cho luôn nghịch biến trên: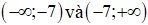

Bài 22. Tìm khoảng nghịch biến của hàm số: .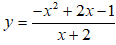

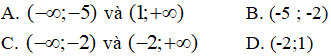
Lời giải:

Đáp án: A

Hàm số đã cho xác định trên: D = R\ {-2}.

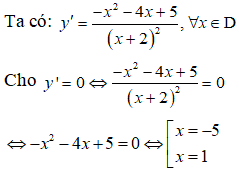
Bảng biến thiên

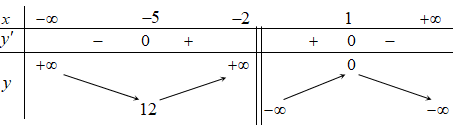
Dựa vào bảng biến thiên, hàm số nghịch biến trên: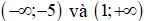

Bài 23. Tìm khoảng đồng biến của hàm số: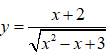

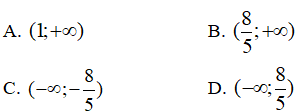
Lời giải:

Đáp án: D

Hàm số đã cho xác định khi: x² - x + 3 > 0 đúng ∀ x ∈ R .

Do đó; hàm số đã cho xác định trên D = R.

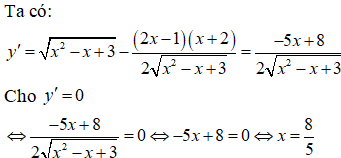
Bảng biến thiên:

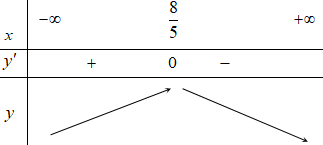
Hàm số đã cho đồng biến trên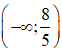

Bài 24. Cho hàm số: y= f(x) = x- sinx, x ∈ [0; π]. Hãy chọn câu đúng

A. Hàm số f(x) đồng biến trên (0; π)

B. Hàm số f(x) nghịch biến trên (0; π)

C. Hàm số f(x) không đổi trên (0; π)

D. Hàm số f(x) nghịch biến trên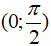

Lời giải:

Đáp án: A

* Hàm số đã cho xác định trên đoạn [0 ; π]

Ta có y’= 1- cosx.

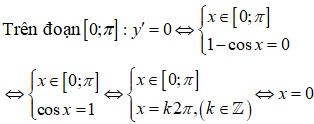
Bảng biến thiên

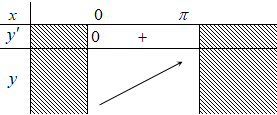
Dựa vào bảng biến thiên, hàm số đã cho đồng biến trên (0; π)

Bài 25. Tìm các khoảng đồng biến của hàm số: y= 2sinx+ cos2x, x ∈ [0; π]

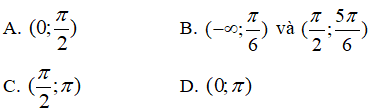
Lời giải:

Đáp án: B

Hàm số đã cho xác định trên đoạn [0; π]

Ta có: y’= 2cosx - 2sin2x = 2cosx- 4. sinx. cosx = 2cosx(1 - 2sinx), x ∈ [0; π]

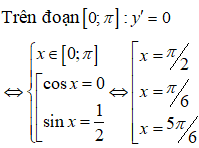
Bảng biến thiên

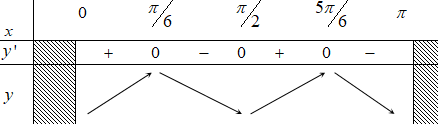
Dựa vào bảng biến thiên, hàm số đồng biến trên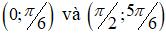

Bài 26. Tìm các khoảng nghịch biến của hàm số: y= sin2x+ cosx, x ∈ [0; π].

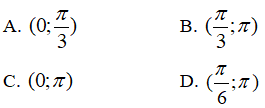
Lời giải:

Đáp án: B

Hàm số đã cho xác định trên đoạn [0; π]

Ta có: y’= 2sinx.cosx - sinx = sinx(2cosx - 1).

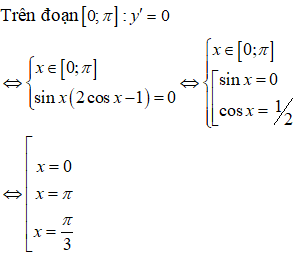
Bảng biến thiên

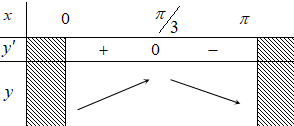
Dựa vào bảng biến thiên, hàm số nghịch biến trên: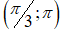

Bài 27. Biết rằng hàm số y= - x³ + 3x- 4 đồng biến trên khoảng (a; b). Tính a+ b?

A. -1     B. 2     C. - 2     D. 0

Lời giải:

Đáp án: D

Tập xác định : D= R. Ta có y’= - 3x² + 3

Xét phương trình y’= 0 ⇔ x = ± 1

Bảng xét dấu y’

Từ bảng xét dấu của y’ ta có hàm số đồng biến trên (-1 ; 1).

Suy ra : a= -1 và b= 1 nên a+ b= 0.

Bài 28. Cho hàm số y= 2x³ + 6x² + 6x- 1995. Mệnh đề nào dưới đây sai?

A. Hàm số đã cho đồng biến trên R.

B. Hàm số đã cho nghịch biến trên R.

C. Trên khoảng 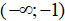hàm số đã cho đồng biến.

D. Trên khoảng 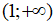hàm số đã cho đồng biến.

Lời giải:

Đáp án: B

+ Tập xác định : D= R.

+ Đạo hàm : y’ = 6x² + 12x + 6 = 6(x+ 1)² ≥ 0; ∀ x ∈ R

(Dấu "=" chỉ xảy ra tại x = - 1)

Suy ra hàm số đồng biến trên R.

Bài 29. Cho hàm số f(x) xác định trên (a;b), với x₁; x₂ bất kỳ thuộc (a;b). Khẳng định nào sau đây là đúng?

A. Hàm số f(x) đồng biến trên (a; b) khi và chỉ khi x₁ < x₂ ⇔ f(x₁) > f(x₂).

B. Hàm số f(x) nghịch biến trên (a; b) khi và chỉ khi x₁ < x₂ ⇔ f(x₁) = f(x₂).

C. Hàm số f(x) đồng biến trên (a; b) khi và chỉ khi x₁ > x₂ ⇔ f(x₁) < f(x₂).

D. Hàm số f(x) nghịch biến trên (a; b) khi và chỉ khi x₁ > x₂ ⇔ f(x₁) < f(x₂) .

Lời giải:

Đáp án: D

Ta xét các phương án:

* A sai. Sửa lại cho đúng là: x₁ < x₂ ⇔ f(x₁) < f(x₂).

* B sai: Sửa lại cho đúng là: x₁ < x₂ ⇔ f(x₁) > f(x₂).

* C sai: Sửa lại cho đúng là: x₁ > x₂ ⇔ f(x₁) > f(x₂).

* D đúng (theo định nghĩa).

Bài 30. Khẳng định nào sau đây là đúng?

A. Hàm số f(x) đồng biến trên (a; b) khi và chỉ khi 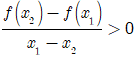với mọi x₁; x₂ ∈ (a; b) và x₁ ≠ x₂.

B. Hàm số f(x) đồng biến trên (a; b) khi và chỉ khi x₂ > x₁ ⇔ f(x₁) > f(x₂).

C. Nếu hàm số f(x) đồng biến trên (a; b) thì đồ thị của nó đi lên từ trái sang phải trên (a; b).

D. Hàm số f(x) đồng biến trên (a; b) thì đồ thị của nó đi xuống từ trái sang phải trên (a; b).

Lời giải:

Đáp án: C

Ta xét các phương án :

* A sai: Sửa lại cho đúng là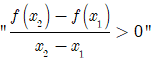

* B sai: Sửa lại cho đúng là: x₂ > x₁ ⇔ f(x₂) > f(x₁).

* C đúng (theo dáng điệu của đồ thị hàm đồng biến).

* D sai (đối nghĩa với đáp án C).