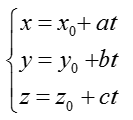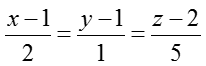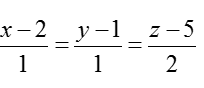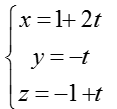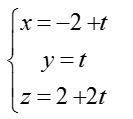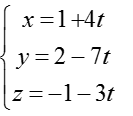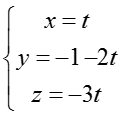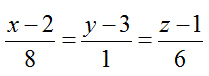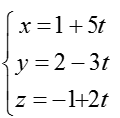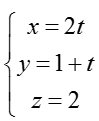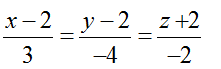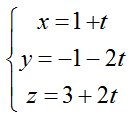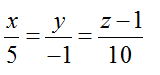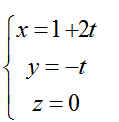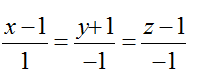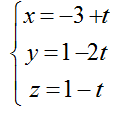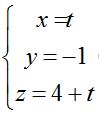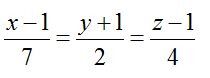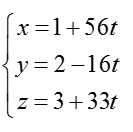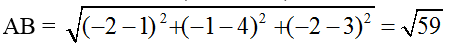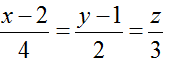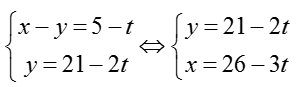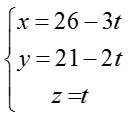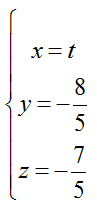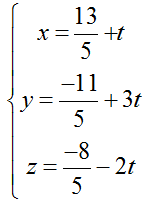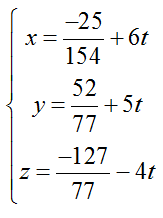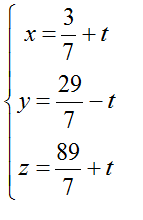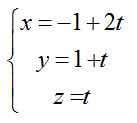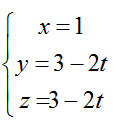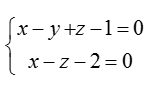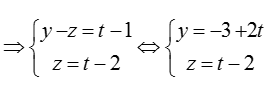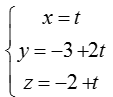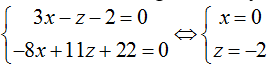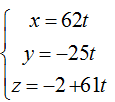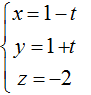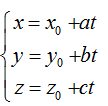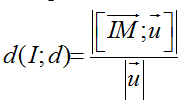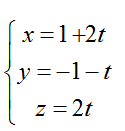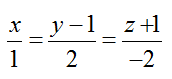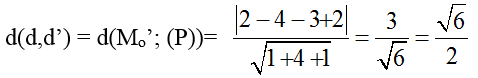Bài tập Viết phương trình đường thẳng trong đề thi Đại học có lời giải (19 dạng) - Toán lớp 12

---

Bài tập Viết phương trình đường thẳng trong đề thi Đại học có lời giải (19 dạng)

Với Bài tập Viết phương trình đường thẳng trong đề thi Đại học có lời giải (19 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Viết phương trình tham số và phương trình chính tắc của đường thẳng d biết d đi qua điểm M và có vectơ chỉ phương u^→ = (a; b; c)

1. Phương pháp giải

Nếu đường thẳng d đi qua điểm M(x_o; y_o; z_o) và vecto chỉ phương u→ ( a; b; c) thì

+ Phương trình tham số của đường thẳng d:

+ Phương trình chính tắc của đường thẳng d ( với a.b.c ≠ 0 ) là:

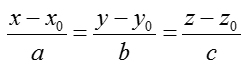
* Chú ý:

+ Nếu đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (α) thì vectơ chỉ phương của đường thẳng d cùng phương với vectơ pháp tuyến của mặt phẳng (α) vì d ⊥(α)

+ Nếu đường thẳng d// ∆ thì đường thẳng d nhận vecto u_d^→ = u_Δ^→ làm vecto chỉ phương .

2. Ví dụ minh họa

Ví dụ 1: Cho đường thẳng ∆ biết ∆ đi qua A (2 ; 1 ; 5) và có vectơ chỉ phương u→=(1;1;2). Tìm mệnh đề đúng

A. Phương trình chính tắc của đường thẳng d:

B. Phương trình tham số của đường thẳng d: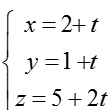

C. Phương trình tham số của đường thẳng d: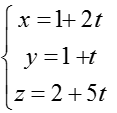

D. Phương trình chính tắc của đường thẳng d: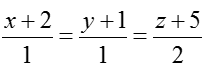

Hướng dẫn giải:

Phương trình tham số của đường thẳng ∆ là:

Trong đó t là tham số

Phương trình chính tắc của đường thẳng ∆ là:

Chọn B.

Ví dụ 2: Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng ∆ đi qua A(1;0; -1) và vuông góc với mặt phẳng (P): 2x - y + z + 9 = 0. Tìm mệnh đề đúng?

A. Vậy phương trình tham số của ∆ là

B. Phương trình chính tắc của ∆ là

C. Vậy phương trình tham số của ∆ là: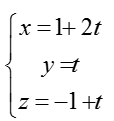

D. Phương trình chính tắc của ∆ là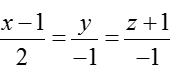

Hướng dẫn giải:

Vì đường thẳng ∆ vuông góc với mặt phẳng (α) nên vectơ chỉ phương của ∆ là:

u_∆→ = n_α→ = (2; -1;1)

Vậy phương trình tham số của ∆ là

Phương trình chính tắc của ∆ là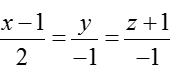

Chọn A.

Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d biết d đi qua A (1; 2; 3) và song song với (d’): 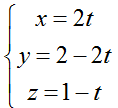. Tìm mệnh đề sai

A. Một vecto chỉ phương của đường thẳng d là u→ ( -4; 4; 2)

B. Vậy phương trình tham số của d là

C. Phương trình chính tắc của d là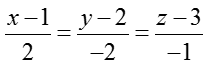

D. đường thẳng d không có phương trình chính tắc

Hướng dẫn giải:

Vì đường thẳng d // d’ nên vectơ chỉ phương của d là: u_d→ = u_d'→ = ( 2; -2; -1)

Vậy phương trình tham số của d là

Phương trình chính tắc của d là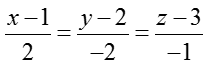

Chọn D.

Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng d biết d đi qua A (0; 2; -1) và song song với (d’): 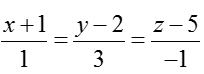. Tìm mệnh đề sai ?

A. Điểm M(2; 8; - 3) thuộc đường thẳng d.

B. Phương trình tham số của đường thẳng d:

C. Đường thẳng d song song với mặt phẳng (P) : x+ 3y- z+ 10= 0

D. Phương trình chính tắc của đường thẳng d: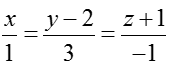

Hướng dẫn giải:

Vì đường thẳng d // d’ nên vectơ chỉ phương của d là: u_d→ = u_d'→ = ( 1; 3; -1)

Vậy phương trình tham số của d là

Cho t= 2 ta được điểm M ( 2; 8; -3) thuộc đường thẳng d

Phương trình chính tắc của d là:

Mặt phẳng (P): x+ 3y – z+ 10= 0 có vecto pháp tuyến n→( 1; 3; -1)

=> Vecto chỉ phương của đường thẳng d là vecto pháp tuyến của măt phẳng (P)

=> đường thẳng d vuông góc với mặt phẳng (P).

=> C sai

Chọn C.

Dạng 2.Viết phương trình đường thẳng d là giao tuyến của hai mặt phẳng cắt nhau (P) và (Q) hoặc đường thẳng d đi qua M và song song với 2 mặt phẳng cắt nhau (P) và (Q).

1. Phương pháp giải

Cách 1:

+ Cả hai trường hợp đều suy ra u_d→⊥n_P→ và u_d→⊥n_Q→

Mà (P) và (Q) cắt nhau nên VTCP của d là u_d→⊥ [n_P→; n_Q→]

+ Tìm một điểm M thuộc đường thẳng d.

+ Đường thẳng d đi qua M và nhận vecto u_d→⊥ [n_P→; n_Q→] làm vecto chỉ phương

=> phương trình tham số và phương trình chính tắc của đường thẳng

Cách 2:

Nếu d là giao tuyến của hai mặt phẳng cắt nhau (P) và (Q) thì với mỗi điểm

M ( x; y;z) thuộc d là nghiệm của hệ phương trình:

phương trình (P) và Phương trình (Q) (*)

Đặt x= t ( hoặc y = t hoặc z = t) thay vào hệ (*) rồi rút y; z theo t

Từ đó suy ra phương trình của đường thẳng d.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ tọa độ Oxyz; gọi d là giao tuyến của hai mặt phẳng (α): x- 3y + z = 0 và (α’): x+y – z +4 = 0. Viết phương trình tham số của đường thẳng d

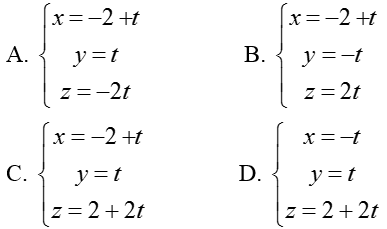
Hướng dẫn giải:

Ta tìm một điểm thuộc đường thẳng d bằng cách cho y = 0 trong hệ (*)

Ta có hệ

Vậy điểm M_o( -2; 0; 2) thuộc đường thẳng d.

Do u_α→ ( 1;-3; 1); n'_α→( 1; 1; -1)

Vectơ chỉ phương của đường thẳng d là u→(1;1;2)

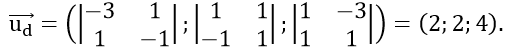
Chọn 1 vectơ chỉ phương của đường thẳng d là u→(1; 1;2)

Vậy phương trình tham số của d là:

Chọn C.

Ví dụ 2: Trong không gian với hệ tọa độ Oxyz; gọi d là giao tuyến của mặt phẳng (P): y – 2z + 3 = 0 và mặt phẳng tọa độ (Oyz).

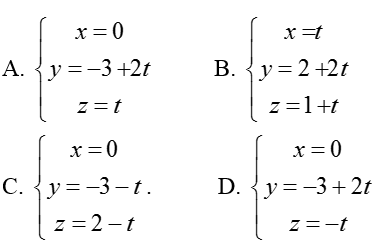Chọn 1 vectơ chỉ phương của đường thẳng d là (1; 1;2)

Hướng dẫn giải:

Mặt phẳng (Oyz) có phương trình x= 0

Điểm M (x; y; z)∈ d khi tọa độ của M là nghiệm của hệ phương trình:

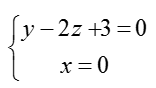
Đặt z= t ta được: 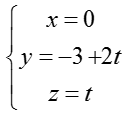là phương trình đường thẳng d

Chọn A.

Ví dụ 3: Viết phương trình đường thẳng d đi qua A (1; 2; - 1) và song song với đường thẳng giao tuyến của hai mặt phẳng (α):x+ y - z + 3= 0 và (α’): 2x – y+ 5z – 4= 0

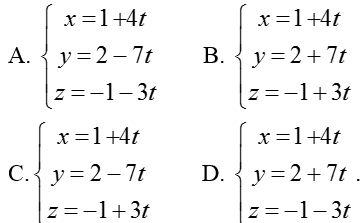
Hướng dẫn giải:

Vecto pháp tuyến của hai mặt phẳng là: n_α→(1; 1; -1); n_α'→(2; -1; 5)

Vectơ chỉ phương của đường thẳng d là

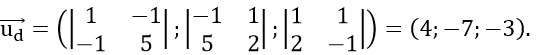
Vậy phương trình đường thẳng d là

Chọn A.

Ví dụ 4: Viết phương trình đường thẳng d là giao tuyến của hai mặt phẳng (α): 2x+ y + 1= 0 và (β): x- y + z – 1 = 0

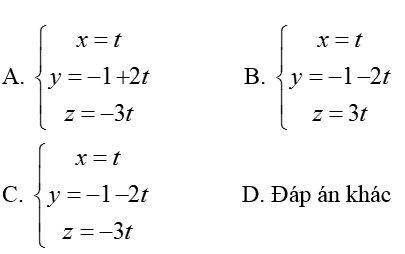
Hướng dẫn giải:

Vecto pháp tuyến của hai mặt phẳng n_α→(2; 1; 0) và n_β→(1; -1; 1)

Vectơ chỉ phương của đường thẳng d là

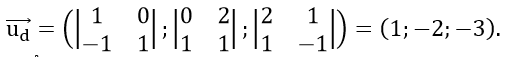
Điểm M (x; y; z) ∈ d khi đó tọa độ của M là nghiệm của hệ phương trình:

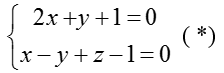
Ta tìm một điểm thuộc đường thẳng d bằng cách cho x = 0 trong hệ (*)

Ta có hệ

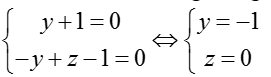
Vậy điểm M_o (0; -1; 0) thuộc đường thẳng d.

Vậy phương trình đường thẳng d là

Chọn C.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng ∆ là giao tuyến của hai mặt phẳng (α): x - 2y – z + 10= 0 và (β): 2x+2y – 3z – 40= 0 . Phương trình đường thẳng d đi qua điểm M(2; 3; 1) và song song với đường thẳng ∆ là

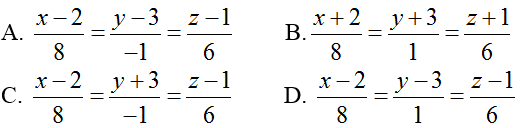
Hướng dẫn giải:

Mặt phẳng (α) có vec tơ pháp tuyến n_α→(1; -2; -1)

Mặt phẳng (β) có vec tơ pháp tuyến n_β→(2; 2; -3)

Đường thẳng d đi qua điểm M và có vectơ chỉ phương là u_d→ = [n_α→;n_α→] =( 8;1; 6)

Vậy phương trình của d là:

Chọn D.

Dạng 3. Viết phương trình đường thẳng d đi qua điểm M, song song với mặt phẳng (P) và vuông góc với đường thẳng d’ (d’ không vuông góc với (P)).

1. Phương pháp giải

Do đường thẳng song song với mặt phẳng ( P) và vuông góc với đường thẳng d’ nên

Suy ra u_d→⊥n_P→ và u_d→⊥ u_d'→

Mà d’ không vuông góc với (P)

Nên VTCP của d là u_d→ = [n_P→;u_d'→]

+ Đường thẳng d đi qua điểm M( đã biết) và nhận vecto u_d→ làm vecto chỉ phương

=> phương trình tham số và phương trình chính tắc của đường thẳng d.

2. Ví dụ minh họa

Ví dụ 1: Viết phương trình đường thẳng d đi qua điểm M (1; 2; -1), song song với mặt phẳng (P): x + y – z = 3 và vuông góc với đường thẳng d’: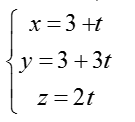

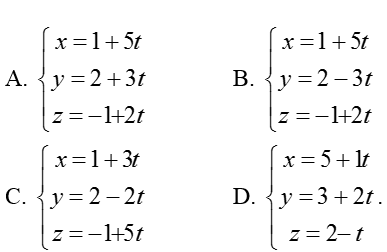
Hướng dẫn giải:

Vecto pháp tuyến của mặt phẳng (P) là n_P→(1; 1; -1)

Vecto chỉ phương của đường thẳng d’ là: u_d'→(1; 3; 2)

Do đường thẳng d song song với mặt phẳng (P) và vuông góc với đường thẳng d’ nên một vecto chỉ phương của đường thẳng d là: u^→ = [n_P^→; u_d'^→] =( 5; -3; 2)

d đi qua điểm M (1; 2; -1)

Vậy phương trình đường thẳng d là

Chọn B.

Ví dụ 2: Viết phương trình đường thẳng d đi qua điểm M (0; 1; 2), song song với mặt phẳng (Oxy) và vuông góc với đường thẳng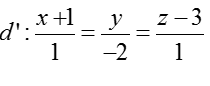

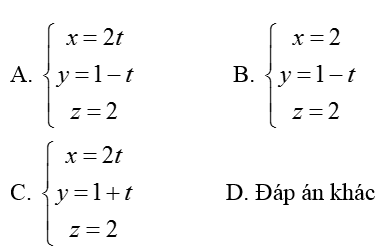
Hướng dẫn giải:

Phương trình mặt phẳng (Oxy) là: z= 0; vecto pháp tuyến của mặt phẳng này là n_Oxy→(0; 0; 1)

Vecto chỉ phương của đường thẳng d’ là u_d'→(1; -2; 1)

Do đường thẳng d song song với mặt phẳng (Oxy) và vuông góc với đường thẳng d’ nên một vecto chỉ phương của đường thẳng d là: u^→ = [u_d'^→;n_Oxy^→] = ( 2; 1; 0)

d đi qua điểm M (0; 1; 2)

Vậy phương trình đường thẳng d là

Chọn C.

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz ; cho mặt phẳng (P) : y- 2z- 1= 0 và đường thẳng ∆ : 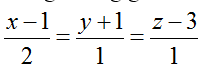. Phương trình chính tắc đường thẳng d đi qua điểm B( 2 ; 2 ; - 2) song song với (P) và vuông góc với ∆ là

Hướng dẫn giải:

Dường thẳng ∆ có vectơ chỉ phương u_∆→(2 ; 1 ;1)

Mặt phẳng (P) có vectơ pháp tuyến n_P→(0 ; 1 ; - 2).

Gọi u_d→ là vectơ chỉ phương của d.

Do đường thẳng d song song với mặt phẳng (P) và vuông góc với đường thẳng ∆ nên một vecto chỉ phương của đường thẳng d là: u_d^→= [n_P^→; u_Δ^→] = ( 3;-4; -2)

Vậy phương trình chính tắc của d là:

Chọn D.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): x- 2y+ 2z- 5= 0 và hai điểm A(0; 0; 1); B( 1; -1; 3). Trong các đường thẳng đi qua A và song song với (P), đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất có phương trình là.

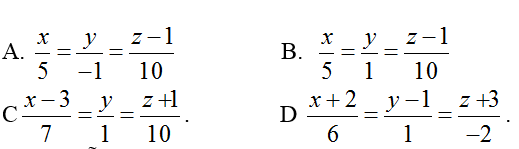
Hướng dẫn giải:

Gọi d là đường thẳng cần tìm

+ Gọi mặt phẳng (Q) qua A( -3; 0;1) và song song với (P).

Khi đó: (Q) có dạng: x- 2y+ 2z + D= 0

Thay tọa độ điểm A vào phương trình ( Q) ta được : -3- 2.0+ 2.1+ D= 0

=> D = 1

Vậy phương trình ( Q): x- 2y + 2z +1= 0

+ Gọi K; H lần lượt là hình chiếu của B lên d; (Q).

Ta có: d( B; d) = BK ≥BH

Do đó AH là đường thẳng cần tìm.

+ Mặt phẳng ( Q) có vectơ pháp tuyến n_Q→(1; -2; 2)

BH qua B và có vectơ chỉ phương u_BH→ = n_Q→(1; -2; 2)

=> Phương trình đường thẳng BH là:

Do H ∈ BH nên H( 1+ t; - 1- 2t; 3+ 2t). Do H thuộc mp (P) nên

1+ t – 2(- 1- 2t) + 2( 3+ 2t ) – 5= 0 => t= -4/9

Do đó H(5/9; -1/9; 19/9)

+ Đường thẳng d đi qua điểm A(0; 0; 1) và có vectơ chỉ phương

u_d→ = AH→ = 1/9(5;-1;10)

Vậy phương trình của d là

Chọn A.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): x- 2y+ 2z- 5= 0; điểm A(2;1; 1); B( -1; 2; 3) . Mặt phẳng (Q) song song với mặt phẳng (P) và đi qua A. Viết phương trình đường thẳng d đi qua M(1;0; 0) đồng thời song song với (P) và vuông góc với đường thẳng OB?

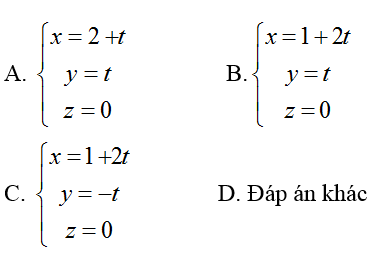
Hướng dẫn giải:

+ Mặt phẳng (Q) qua A(2; 1;1) và song song với (P).

Khi đó (Q) có dạng: x- 2y+ 2z + D= 0

Thay tọa độ điểm A vào phương trình ( Q) ta đưọc: 2- 2.1 + 2.1+ D= 0

=> D = - 2

Vậy phương trình ( Q): x- 2y +2z - 2= 0

Mặt phẳng ( Q) có vecto pháp tuyến n→(1; -2; 2)

+ Đường thẳng OB có vecto chỉ phương là OB→( -1; 2; 3)

+ Đường thẳng d đi qua điểm M(1;0 ; 0) và có vectơ chỉ phương là :

u→ = [n→; OB→] = ( -10; 5; 0) = - 5( 2; -1; 0)

Vậy phương trình của d là

Chọn C.

Dạng 4. Viết phương trình đường thẳng d đi qua một điểm M; nằm trong mặt phẳng (P) và vuông góc với đường thẳng ∆ (hoặc song song với mặt phẳng (Q) ).

1. Phương pháp giải

+ Tìm vecto chỉ phương của đường thẳng ∆: u_∆→

+ Tìm vecto pháp tuyến của mặt phẳng (P) và (Q): n_P→; n_Q→

+ Trong cả hai trường hợp ta đều có một vecto chỉ phương của đường thẳng d là:

u→ = [u_∆→; n_P→] hoặc [n_P→; n_Q→]

+ Khi đó; đường thẳng d: đi qua điểm M và có vecto chỉ phương u→

=> phương trình đường thẳng d:

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng ∆: và mặt phẳng (P): x- 2y+ 3z+ 10 = 0. Viết phương trình đường thẳng d đi qua M( 1; -1; 1); nằm trong mặt phẳng (P) và vuông góc với đường thẳng ∆?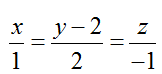

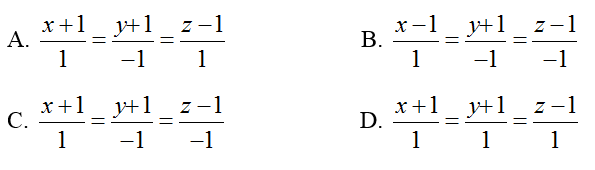
Hướng dẫn giải:

+ Đường thẳng ∆ có vecto chỉ phương u_∆→( 1; 2; -1)

Mặt phẳng ( P) có vecto pháp tuyến n→( 1; -2; 3).

+ Do đường thẳng d nằm trong mặt phẳng (P) và vuông góc với đường thẳng ∆ nên một vecto chỉ phương của đường thẳng d là:

u→ = [u_∆→; n→] = ( 4; - 4; - 4) chọn ( 1; -1; -1) .

=> Phương trình đường thẳng d cần tìm

Chọn B.

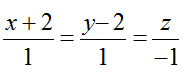
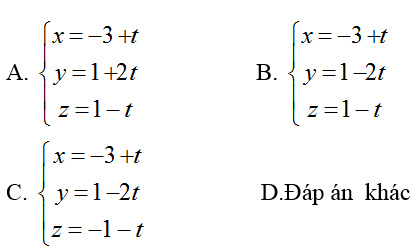
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng ∆ : và mặt (P): x+ 2y – 3z+ 4= 0. Phương trình tham số của đường thẳng d nằm trong (P) , cắt và vuông góc đường thẳng ∆ là:

Hướng dẫn giải:

+ Tìm giao điểm M của ∆ và mặt phẳng ( P):

Điểm M( - 2+ t; 2+ t;- t) thuộc ∆.

Thay tọa độ M vào phương trình (P) ta được:

- 2+ t+ 2(2+ t) – 3( - t) + 4= 0 ⇔ - 2+ t + 4 + 2t + 3t + 4= 0

⇔ 6t+ 6= 0 nên t= -1 => M ( - 3; 1; 1)

+ Mặt phẳng (P) có vectơ pháp tuyến u_P→( 1; 2;-3)

+ Đường thẳng ∆ có vectơ chỉ phương u_∆→( 1; 1; -1)

+ Do đường thẳng d nằm trong mặt phẳng (P)và vuông góc với đường thẳng ∆ nên một vecto chỉ phương của đường thẳng d là : u^→=[n_P^→;u_∆^→] = (1; -2; -1)

+ Đường thẳng d đi qua điểm M( -3; 1; 1) và có vectơ chỉ phương là u→ = (1; -2; -1)

Vậy phương trình tham số của d là:

Chọn B.

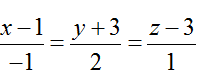
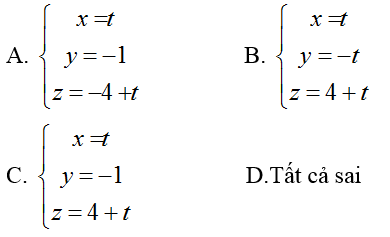
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng d: và mặt phẳng (P): 2x+ y- 2z + 9= 0. Gọi A là giao điểm của d và (P). Phương trình tham số của đường thẳng ∆ nằm trong (P), đi qua điểm A và vuông góc với d là

Hướng dẫn giải:

+ Điểm A là giao điểm của đường thẳng d và (P).

=> Tọa độ A( 1- t; - 3+ 2t; 3+ t)

Thay tọa độ điểm A vào phương trình mặt phẳng (P) ta được :

2( 1- t) + ( -3+ 2t) – 2( 3+ t) + 9= 0

⇔ 2- 2t- 3+ 2t – 6 – 2t + 9= 0 ⇔ - 2t+ 2= 0

⇔ t= 1 nên A(0; -1; 4)

+ Mặt phẳng ( P) có vectơ pháp tuyến n_P→( 2; 1; - 2)

+ Đường thẳng d có vectơ chỉ phương u_d→( -1;2; 1)

+ Do đường thẳng ∆ nằm trong (P) và vuông góc với d nên một vecto chỉ phương của ∆ là:

u→ = [n_P→;u_d→] = (5; 0; 5) chọn ( 1; 0;1)

+ Đường thẳng ∆ đi qua điểm A(0; - 1; 4) và có vectơ chỉ phương là ( 1; 0;1)

Vậy phương trình tham số của ∆

Chọn C.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho hai điểm A( -1; -1; -1) và B(1;2;0). Mặt phẳng (P): 3x- 2y+ z- 10= 0 . Đường thẳng d đi qua M( -1; 2;2) nằm trong mặt phẳng (P) và vuông góc với đường thẳng AB. Trong các đường thẳng sau đường thẳng nào song song với đường thẳng d?

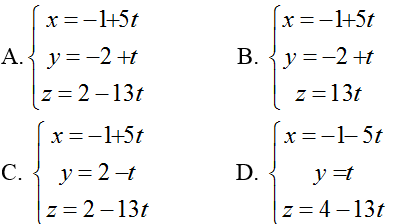
Hướng dẫn giải:

+ Đường thẳng AB có vecto chỉ phương AB→( 2; 3; 1)

+ Mặt phẳng (P) có vecto pháp tuyến n→(3; -2; 1) .

+ Do đường thẳng d nằm trong mặt phẳng (P) và vuông góc với đường thẳng AB nên một vecto chỉ phương của đường thẳng d là [AB^→; n^→] = (5; 1; -13)

=> Phương trình đường thẳng d:

=> Đường thẳng d’: song song với đường thẳng d( có cùng vecto chỉ phương và điểm M không thuộc đường thẳng d’) .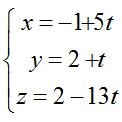

Chọn A.

Dạng 5. Viết phương trình đường thẳng ∆ đi qua A; cắt d và song song với mặt phẳng (P)

1. Phương pháp giải

+ Gọi giao điểm của đường thẳng d và ∆ là M

=> Tọa độ của M( ..) ( theo tham số t; dựa vào phương trình đường thẳng d) .

=> Đường thẳng ∆ nhận vecto AM→( ....) làm vecto chỉ phương.

+ Mặt phẳng (P) có vecto pháp tuyến n→

+ Do đường thẳng ∆ song song với mặt phẳng (P) nên ta có; n→.u→ = 0 => Phương trình ẩn t

=> t=...=> tọa độ điểm M

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ tọa độ Oxyz; cho điểm A(1; 2; -1) và đường thẳng d: 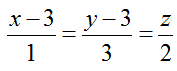. Phương trình đường thẳng đi qua điểm A, cắt d và song song với mặt phẳng (Q): x+ y- z+ 3= 0 là:

Hướng dẫn giải:

Gọi ∆ là đường thẳng cần tìm

+ Gọi giao điểm của hai đường thẳng d và ∆ là B .

Do B thuộc d nên B( 3+ t; 3+ 3t; 2t) => AB→( 2+ t;1+ 3t; 2t+ 1)

+ Mặt phẳng ( Q) có vectơ pháp tuyến n_Q→( 1; 1; -1)

+ Do đường thẳng ∆ song song với mặt phẳng (Q) nên AB→⊥n_Q→

=> AB^→. n_Q^→ ⇔ 1( 2+ t)+ 1( 1+ 3t)- 1( 2t+ 1) = 0

⇔ 2+ t+1+ 3t – 2t- 1= 0 ⇔ 2t + 2= 0

⇔ t= - 1

+ Đường thẳng ∆ đi qua A( 1; 2; -1) và nhận vecto AB→(1; - 2; - 1) làm vecto chỉ phương nên phương trình của ∆ là:

Chọn A.

Ví dụ 2: Cho hai điểm A( 1;1;0) và B( 2; -1; 2). Viết phương trình đường thẳng d đi qua M(1;0;0) cắt đường thẳng AB và song song với mặt phẳng (P): 2x+ y+ z- 1= 0.

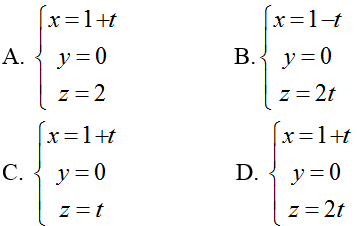
Hướng dẫn giải:

+ Đường thẳng AB: đi qua A( 1; 1;0); nhận vectơ AB→(1; -2; 2) làm vecto chỉ phương

=> Phương trình AB:

+ Gọi giao điểm của đường thẳng d và AB là H(1+ t; 1-2t;2t)

+ đường thẳng d nhận vecto MH→( t; 1- 2t; 2t ) làm vecto chỉ phương .

+ Mặt phẳng (P) nhận vecto n→( 2; 1;1) làm vecto pháp tuyến.

+ Do đường thẳng d song song với mặt phẳng (P) nên MH→.n→ = 0 ⇔ 2t + 1( 1- 2t) + 1.2t= 0

⇔ 2t+ 1= 0 ⇔ t= 1/2 => H(3/2;0;1)

+ Đường thẳng d đi qua M( 1; 0;0) và nhận vecto MH→(1/2;0;1) làm vecto chỉ phương; chọn vecto ( 1; 0; 2)

=> Phương trình đường thẳng d:

Chọn D.

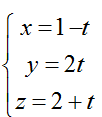
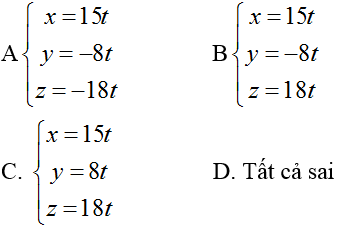
Ví dụ 3: Cho đường thẳng d: ba điểm A(1;1;1); B( -2; 1; -1) và C( 1; 0;2). Viết phương trình đường thẳng ∆ qua O cắt d và song song với mặt phẳng (ABC)

Hướng dẫn giải:

+ Ta có: AB→(-3; 0; -2); BC→(3; -1; 3)

Mặt phẳng (ABC) nhận vecto n→[AB→;BC→] = ( -2; 3;3) làm vecto pháp tuyến.

+ Gọi giao điểm của đường thẳng d và ∆ là M( 1-t; 2t; 2+ t)

Đường thẳng ∆ nhận vecto OM→( 1-t; 2t; 2+t) làm vecto chỉ phương

+ Do đường thẳng d song song với mặt phẳng (ABC) nên: n→. OM→ = 0

⇔ -2(1- t) + 3.2t + 3.( 2+ t) = 0 ⇔ - 2+ 2t+ 6t+ 6+ 3t = 0

⇔ 11t+ 4= 0 ⇔ t = -4/11

+ Đường thẳng OM: qua O nhận vecto OM→(15/11; -8/11; 18/11) làm VTCP chọn n→(15; - 8;18)

=> Phương trình OM:

Chọn B.

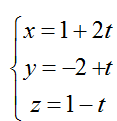
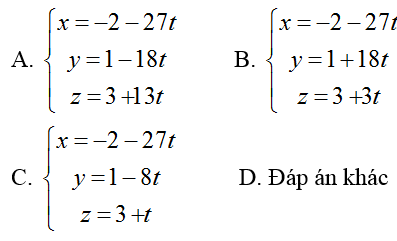
Ví dụ 4: Cho đường thẳng d: và mặt phẳng (P): 2x- 3y- 1= 0. Viết phương trình đường thẳng ∆ đi qua M( -2; 1; 3) cắt đường thẳng d và song song với mặt phẳng (P).

Hướng dẫn giải:

+ Mặt phẳng (P) có vecto pháp tuyến n→(2; -3; 0).

+ Gọi giao điểm của đường thẳng d và ∆ là A( 1+2t; - 2+ t;1- t).

+ Đường thẳng ∆ nhận vecto MA→( 3+ 2t; - 3+ t; -2- t) làm vecto chỉ phương.

Do đường thẳng ∆ song song với mặt phẳng (P) nên MA→.n→ = 0

⇔ 2( 3+ 2t) – 3( - 3+ t) + 0( - 2- t) = 0

⇔ 6+ 4t+ 9 – 3t = 0 ⇔t= -15

+ Đường thẳng ∆: đi qua M( -2; 1; 3) và nhận vecto MA→(- 27; -18; 13) làm vecto chỉ phương nên phương trình

Chọn A.

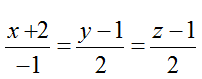
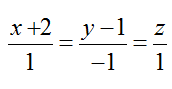
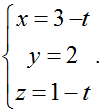
Ví dụ 5: Cho mặt phẳng (P) chứa đường thẳng d₁ : và song song với d₂: . Đường thẳng d có phương trình: . Gọi đường thẳng ∆ đi qua M( 0; -1; 1); cắt d và song song với (P). Tìm giao điểm của đường thẳng d và ∆?

A. ( - 4; 2; -6)    B. (1; 2; - 1)     C. ( 0; 2; - 2)    D. (6; 2; 4)

Hướng dẫn giải:

+ Đường thẳng d₁ có vecto chỉ phương u₁→(-1; 2; 2) và đi qua A(-1; 2; 2)

+ Đường thẳng d₂ có vecto chỉ phương u₂→(1; -1; 1)

=> Mặt phẳng (P) có vecto pháp tuyến n→= [u₁→; u₂→] = ( 4; 3; -1).

+ Gọi giao điểm của d và ∆ là H( 3- t; 2; 1- t )

Đường thẳng ∆ nhận vecto MH→(3- t; 3; - t ) làm vecto chỉ phương.

+ Do đường thẳng ∆ song song với (P) nên: n→. MH→ = 0

⇔ 4(3- t)+ 3. 3 – 1( -t) = 0

⇔ 12- 4t +9 + t= 0 ⇔ 21- 3t= 0 ⇔t= 7

=> Giao điểm của đường thẳng d và ∆ là H( - 4; 2; - 6)

Chọn A.

Dạng 6. Viết phương trình đường thẳng d đi qua điểm M và vuông góc với hai đường thẳng d₁ và d₂ (d₁ và d₂ là hai đường thẳng chéo nhau).

1. Phương pháp giải

+ Gọi u_d→; u_d1→; u_d2→ lần lượt là vecto chỉ phương của đườg thẳng d; d₁ và d₂

+ Do đường thẳng d vuông góc với cả hai đường thẳng d₁ và d₂ nên u_d→⊥u_d1→; u_d→⊥u_d2→

+ Mà d₁ và d₂ chéo nhau

=> Vecto chỉ phương của d là u_d→ = [u_d1→; u_d2→]

Sau đó, áp dụng định nghĩa phương trình tham số và phương trình chính tắc của đường thẳng

2. Ví dụ minh họa

Ví dụ 1: Viết phương trình đường thẳng d đi qua A (2; -1; 1) và vuông góc với hai đường thẳng lần lượt có vectơ chỉ phương là u₁^→(-1; 1; -2) và u₂^→(1; -2; 0)

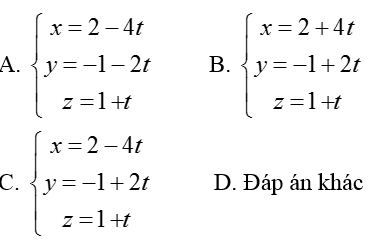
Hướng dẫn giải:

Do đường thẳng d vuông góc với 2 đường thẳng lần lượt có vecto chỉ phương là u₁→; u₂→ nên một vectơ chỉ phương của đường thẳng d là u→= [u₁→; u₂→] = (-4; -2; 1)

d đi qua điểm A (2; -1; 1)

Vậy phương trình đường thẳng d là

Chọn A.

Ví dụ 2: Viết phương trình đường thẳng d đi qua A (1; 2; 3) và vuông góc với hai đường thẳng

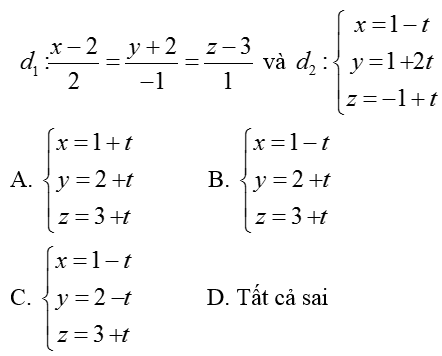
Hướng dẫn giải:

+ Vecto chỉ phương của hai đường thẳng d₁; d₂ lần lượt là u₁→( 2; -1; 1) và u₂→(-1; 2; 1)

+ Do đường thẳng d vuông góc với 2 đường thẳng lần lượt có vecto chỉ phương là u₁→; u₂→

Nên 1 VTCP của đường thẳng d là u_d→ = [u₁→; u₂→] = (- 3; -3; 3), chọn VTCP (-1; -1; 1)

Mà d đi qua điểm A (1; 2; 3) nên phương trình đường thẳng d là

Chọn C

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz ; cho hai điểm A(1 ;-1 ;1) ; B(-1 ; 2 ; 3) và đường thẳng ∆ : 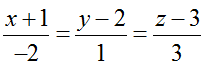. Phương trình đường thẳng d đi qua điểm A, đồng thời vuông góc với hai đường thẳn AB và ∆ là

Hướng dẫn giải:

Ta có: AB→( -2; 3; 2).

Đường thẳng ∆ có vectơ chỉ phương u_∆→( -2; 1; 3)

Do đường thẳng d vuông góc với hai đường thẳng AB và ∆ nên một vecto chỉ phương của đường thẳng d là: u→ = [u_∆→; AB→] = ( -7;-2; -4) chọn vecto ( 7;2; 4)

Vậy phương trình chính tắc của d là:

Chọn B.

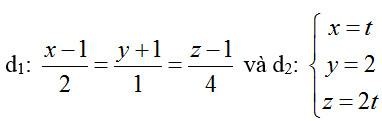
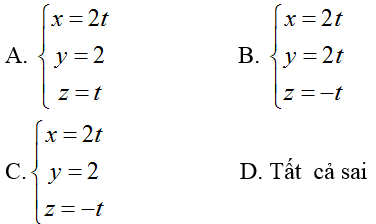
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng . Phương trình đường thẳng ∆ đi qua điểm A(0;2; 0) và vuông góc với hai đường thẳng d₁; d₂ là

Hướng dẫn giải:

Đường thẳng d₁ có vectơ chỉ phương u₁→( 2; 1; 4)

Đường thẳng d₂ có vectơ chỉ phương u₂→(1;0; 2)

Do đường thẳng ∆ vuông góc với hai đường thẳng d₁ và d₂ nên một vecto chỉ phương của đường thẳng ∆ là: u→ = [u₁→; u₂→] = ( 2;0;-1)

Vậy phương trình tham số của ∆ là

Chọn C.

Dạng 7. Viết phương trình đường thẳng d đi qua điểm M đồng thời cắt cả hai đường thẳng d₁ và d₂

1. Phương pháp giải

Cách 1:

• Bước 1: Viết phương trình mặt phẳng α đi qua điểm M và chứa đường thẳng d₁

• Bước 2: Tìm giao điểm A = α ∩ d₂

• Bước 3: Đường thẳng cần tìm là đường thẳng đi qua 2 điểm M, A

Cách 2:

• Bước 1: Viết phương trình mặt phẳng (α) đi qua điểm M và chứa đường thẳng d₁

• Bước 2: Viết phương trình mặt phẳng (β) đi qua điểm M và chứa đường thẳng d₂

• Bước 3: Đường thẳng cần tìm d = α ∩ β

Cách 3:

Gọi A, B lần lượt là giao điểm của d và d₁, d và d₂

Đường thẳng d đi qua M nên A, B, M thẳng hàng

=> MA→; MB→ cùng phương nên MA→ = k.MB→

2. Ví dụ minh họa

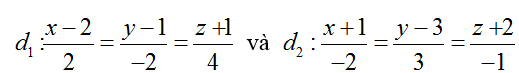
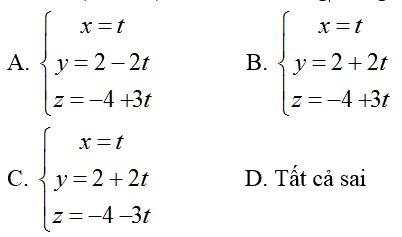
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz. Cho đường thẳng . Viết phương trình đường thẳng ∆ đi qua điểm A(0; 2; -4) và cắt hai đường thẳng d₁ và d₂

Hướng dẫn giải:

+ Gọi (P) là mặt phẳng đi qua A và chứa d₁

Đường thẳng d₁ qua B( 2 ; 1 ; -1) và có vecto chỉ phương u_d1→(2 ;-2 ; 4)

Ta có AB→(2 ; -1 ;3)

Mặt phẳng (P) có một vecto phap tuyến là [u_d1→; MA→] = (-2 ; 2 ; 2)

+ Gọi (Q) là mặt phẳng đi qua A và chứa d₂

Đường thẳng d₂ qua C(-1; 3; -2) và có vecto chỉ phương u_d2→(-2; 3;-1)

Ta có: AC→(- 1; 1;2)

Mặt phẳng (Q) có một vecto phap tuyến là [u_d2→; AC→] = ( 7; 5; 1)

+ Khi đó đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (P) và (Q).

=> Một vecto chỉ phương của đường thẳng ∆ là [n_P→; n_Q→] = (-8; 16; -24) = -8( 1; -2; 3)

Do vậy phương trình ∆ là:

Chọn A.

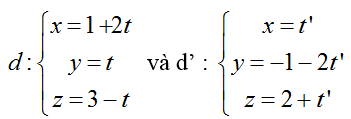
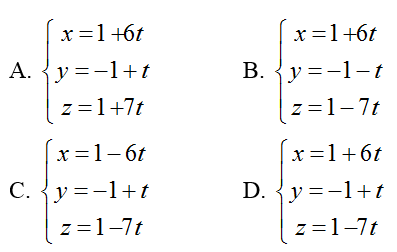
Ví dụ 2: Phương trình đường thẳng ∆ đi qua và cắt cả hai đường thẳng là :

Hướng dẫn giải:

Chọn D

+ Gọi (P) là mặt phẳng chứa đường thẳng d và đi qua điểm A.

Đường thẳng d đi qua điểm B( 1;0 ;3) và có vecto chỉ phương u₁→( 2 ; 1 ; -1)

Ta có AB→(0 ;1 ; 2)

Mặt phẳng (P) có một vecto pháp tuyến là n₁→ = [u₁→; AB→] = ( 3 ; -4 ; 2).

+ Gọi (Q) =là mặt phẳng đi qua A và chứa d’

Đường thẳng d’ qua C( 0; -1; 2) và có vecto chỉ phương u₂→(1; -2; 1)

Ta có AC→( -1; 0; 1)

Mặt phẳng (Q) có một vecto pháp tuyến là n₂→ = [u₂→; AC→] = ( -2 ; -2 ; -2)

+ Đường thẳng ∆ là giao tuyến của hai mặt phẳng (P) và (Q) nên đường thẳng ∆ có vectơ chỉ phương là [n₁→;n₂→] = (12; 2; -14) = 2( 6; 1; -7) và đi qua A nên có phương trình tham số là:

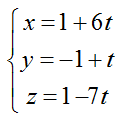
Chọn D.

Ví dụ 3: Viết phương trình đường thẳng d đi qua M (1; 1; 0) và cắt hai đường thẳng:

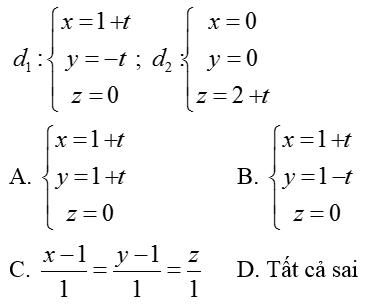
Hướng dẫn giải:

Chọn A.

- Một điểm thuộc d₁ là : A (1; 0; 0)

=> MA→(0; -1; 0)

Mặt phẳng α đi qua điểm M và chứa đường thẳng d₁ có VTPT là u_α→ = [MA→; u_d1→] = (0; 0; 1)

Phương trình mặt phẳng α là:

0.(x – 1) + 0. (y – 1) + 1. (z – 0) = 0 hay z = 0

- Giao điểm B = α ∩ d₂ là (0; 0; 0)

- Đường thẳng cần tìm là đường thẳng đi qua 2 điểm M, B

Vectơ chỉ phương của d là BM→(1;1; 0)

Vậy phương trình đường thẳng d là:

Ví dụ 4: Viết phương trình đường thẳng d biết d đi qua điểm A (1; 2; 3) và cắt hai đường thẳng

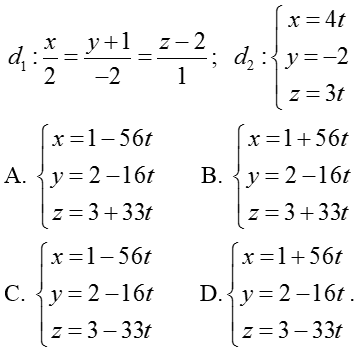
Hướng dẫn giải:

- Đường thẳng d₁ có vecto chỉ phương u_d1→(2; -2; 1). Một điểm M thuộc d₁ là M (0; -1; 2)

=> MA^→(1; 3; 1)

Mặt phẳng α đi qua điểm A và chứa đường thẳng d₁ có vectơ pháp tuyến là:

n_α→ = [MA→; u₁→] = ( 5;1; -8)

- Đường thẳng d₂ có vecto chỉ phương u₂→(4; 0; 3). Một điểm thuộc d₂ là N (0; -2; 0)

=> NA→( 1; 4; 3)

Mặt phẳng β đi qua điểm A và chứa đường thẳng d₂ có VTPT là n_β→ = [NA→; u₂→] =(12; 9; -16)

- Đường thẳng cần tìm d = (α) ∩ (β)

Vectơ chỉ phương của d là u_d→ = [n_α→; n_β→] = ( 56, -16, 33)

Vậy phương trình đường thẳng d là:

Chọn B.

Dạng 8. Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng d₁ và cắt đường thẳng d₂.

1. Phương pháp giải

Cách 1:

- Viết PT mặt phẳng (P) đi qua A và vuông góc với đường thẳng d₁

- Tìm giao điểm B = (P) ∩ d₂

- Đường thẳng cần tìm là đường thẳng đi qua 2 điểm A, B

Cách 2:

- Viết PT mặt phẳng (P) đi qua A và vuông góc với đường thẳng d₁

- Viết PT mặt phẳng (Q) đi qua A và chứa đường thẳng d₂

- Đường thẳng d cần tìm là d = (P) ∩ (Q)

2. Ví dụ minh họa

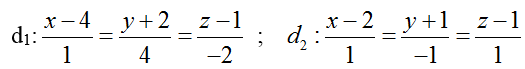
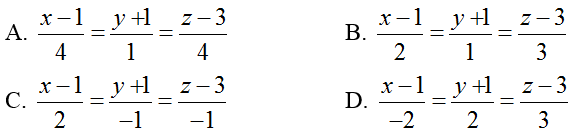
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, cho điểm A( 1; - 1; 3) và hai đường thẳng .Viết phương trình đường thẳng d đi qua điểm A vuông góc với đường thẳng d₁ và cắt đường thẳng d₂.

Hướng dẫn giải:

+ Gọi ( P) là mặt phẳng qua A vuông góc với đương thẳng d₁.

Đường thẳng d₁ có vecto chỉ phương là ( 1; 4; -2) nên một vecto pháp tuyến của mặt phẳng (P) là: n→( 1; 4; -2)

=> Phương trình mặt phẳng (P) là: 1( x-1) + 4( y+1) – 2( z- 3) =0

Hay x+ 4y – 2z + 9= 0

+Gọi giao điểm của đường thẳng d₂ và mặt phẳng ( P) là điểm B

Do B thuộc d₂ nên tọa độ B( 2+ t; - 1- t; 1+ t) . Thay tọa độ điểm B vào phương trình mặt phẳng (P) ta được : 2+ t + 4( - 1- t) – 2( 1+ t) + 9= 0

⇔ 2+ t- 4 – 4t- 2- 2t + 9= 0

⇔ - 5t+ 5= 0 ⇔ t= 1

=> B( 3; -2; 2)

+ Đường thẳng d cần tìm là đường thẳng AB: Đi qua A(1; -1;3) nhận vecto AB→(2; -1;- 1)

=> Phương trình chính tắc của đường thẳng AB:

Chọn C.

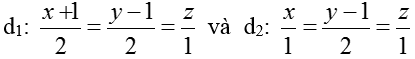
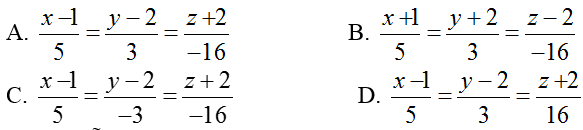
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng . Phương trình đường thẳng d đi qua điểm A( 1; 2; -2) vuông góc với d₁ và cắt d₂ là:

Hướng dẫn giải:

+ Gọi giao điểm của của d và d₂ là B.

Do B thuộc d₂ nên tọa độ B( t; 1+ 2t; t) => AB→( t- 1; 2t- 1; t+ 2) .

+ Đường thẳng d₁ có vectơ chỉ phương u₁→ ( 2; 2; 1)

+ Do đường thẳng d vuông góc với d₁ nên AB→ ⊥u₁→

AB→ . u₁→ = 0

⇔ 2( t-1) + 2( 2t- 1) + 1(t+ 2) = 0

⇔ 2t – 2 + 4t – 2+ t+ 2= 0

⇔ 7t- 2= 0 nên t = 2/7

+ Đường thẳng d đi qua điểm A ( 1; 2; - 2) và có vectơ chỉ phương AB→(-5/7; -3/7; 16/7)

chọn vecto chỉ phương ( 5; 3; - 16)

Vậy phương trình của d là

Chọn A.

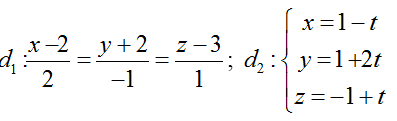
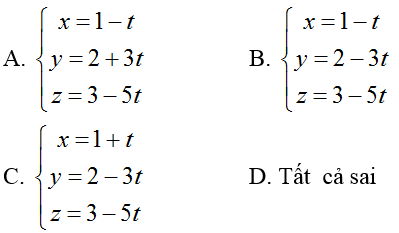
Ví dụ 3: Cho hai đường thẳng ; và điểm A (1; 2; 3). Viết phương trình đường thẳng d đi qua A,vuông góc với d₁và cắt d₂.

Hướng dẫn giải:

- Gọi mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng d₁ có VTPT là n_P→ = u_d1→

=> n_P→ = (2; -1; 1)

Phương trình mặt phẳng (P) là:

2.(x – 1) – 1 . (y – 2) + 1. (z – 3) = 0 hay 2x – y + z – 3 = 0

-Gọi giao điểm của mặt phẳng (P) và đường thẳng d₂ là B

B thuộc d₂ nên tọa độ B( 1- t; 1+ 2t; - 1+ t)

Thay tọa độ ( B) vào phương trình mặt phẳng (P) ta được:

2( 1- t) – ( 1+ 2t) + ( - 1+ t) – 3= 0

⇔ 2- 2t- 1- 2t- 1+ t- 3= 0

⇔ -3t – 3= 0 nên t= -1

Suy ra: B (2; -1; -2)

- Đường thẳng cần tìm là đường thẳng đi qua 2 điểm A, B

Vectơ chỉ phương của d là: AB→(1; -3; -5)

Vậy phương trình đường thẳng d là:

Chọn C.

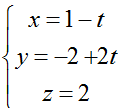
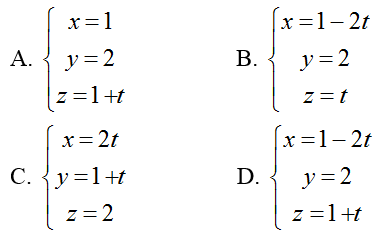
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho điểm A(-1; 2; 0); B( 2; 1;1) và C( 2; 3; 2). Gọi G là trọng tâm của tam giác ABC. Đường thẳng d đi qua G vuông góc với trục tung và cắt đường thẳng ∆: . Viết phương trình đường thẳng d?

Hướng dẫn giải:

+ Do G là trọng tâm của tam giác ABC nên tọa độ G( 1; 2;1) .

+ Gọi giao điểm của đường thẳng d và ∆ là: H( 1- t; - 2+ 2t; 2) => GH→(- t; 2t- 4; 1)

Ta có vecto chỉ phương của trục tung là u_Oy→(0; 1; 0) .Khi đó:

Do d⊥Oy ⇔ GH→.u_Oy→ = 0 ⇔ 0. ( -t) + 1(2t- 4)+ 0.1= 0

⇔2t – 4 = 0 ⇔ t = 2 nên tọa độ H( -1; 2; 2)

+ Đường thẳng d cần tìm là đường thẳng GH: đi qua G( 1; 2; 1) và VTCP GH→(-2; 0; 1)

=> Phương trình đường thẳng d:

Chọn D.

Dạng 9. Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng d₁ và cắt đường thẳng d₁.

1. Phương pháp giải

Gọi giao điểm của đường thẳng d và d₁ là B.

+ Vì B thuộc đường thẳng d₁ nên tọa độ B có dạng... ( theo tham số t).

=> Tọa độ AB→

+ Xác định vecto chỉ phương của u₁→ đường thẳng d₁.

+ Do đường thẳng d vuông góc với đường thẳng d₁ nên AB→⊥ u₁→

=> AB→.u₁→ = 0

=>Phương trình ẩn t ....=> t= ...

=> Tọa độ điểm B.

+ Viết phương trình đường thẳng d đi qua hai điểm A và B.

2. Ví dụ minh họa

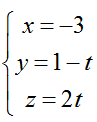
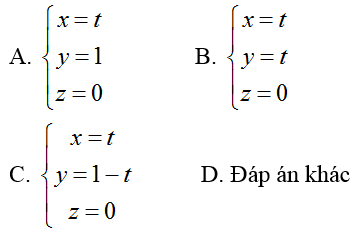
Ví dụ 1: Cho đường thẳng d₁ có phương trình tham số và điểm A(0;1; 0). Phương trình tham số đường thẳng d đi qua điểm A đồng thời vuông góc và cắt đường thẳng d₁ là:

Hướng dẫn giải:

+ Đường thẳng d₁ có vecto chỉ phương là u₁→( 0; -1; 2)

Gọi giao điểm của đường thẳng d và d₁ là B.

+ Vì B thuộc đường thẳng d₁ nên tọa độ B có dạng B( -3; 1-t; 2t)

=> AB→ (-3; - t; 2t)

Vì đường thẳng d vuông góc với đường thẳng d₁ nên ta có

⇔ AB→.u₁→ = 0 ⇔ 0. (-3) – 1( - t) + 2.2t= 0

⇔ 5t = 0 ⇔ t = 0

Suy ra tọa độ B( - 3; 1; 0)

+ Đường thẳng cần tìm chính là đường thẳng AB: đi qua A( 0;1; 0) và có VTCP AB→( -3;0; 0) chọn u→(1; 0; 0).

Vậy phương trình tham số của đường thẳng d là

Chọn A.

Ví dụ 2: Cho điểm A( -1; -2; 3) và đường thẳng d: 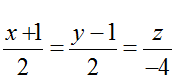. Đường thẳng ∆ đi qua cắt và vuông góc với đường thẳng d. Tìm một vecto chỉ phương của đường thẳng ∆

A . (4; 4; 0)    B. (2; -2; 1)

C. ( 2;4; 1)    D. ( 3; -3;0)

Hướng dẫn giải:

Gọi giao điểm của đường thẳng d và ∆ là M

Khi đó M ∈ d => M( - 1+ 2t; 1+ 2t; - 4t) => AM→(2t; 3+ 2t; - 4t – 3)

Đường thẳng d có vecto chỉ phương là u_d→ (1; 1; -2).

Khi đó; ∆⊥d => AM→⊥u_d→ => AM→ .u_d→ = 0

⇔ 1. 2t+ 1( 3+ 2t) – 2( - 4t- 3) =0

⇔ 2t+ 3+ 2t+ 8t+ 6 = 0⇔ 12t + 9= 0

⇔ t = -3/4

Suy ra, AM→(-3/2;3/2;0) là một vecto chỉ phương của đường thẳng d.

Chọn D.

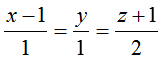
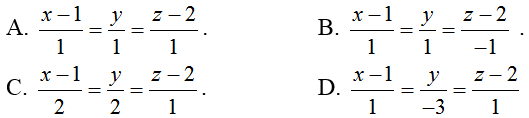
Ví dụ 3: Trong không gian với hệ toạ độ Oxyz,cho điểm A(1; 0;2) và đường thẳng d có phương trình . Viết phương trình đường thẳng ∆ đi qua A vuông góc và cắt d

Hướng dẫn giải:

Ta có u_d→(1; 1; 2) là một vecto chỉ phương của đường thẳng d.

Gọi ∆ ∩ d = B=> B ∈ d => B(1+ t; t; -1+ 2t) => AB→ ( t; t; 2t – 3)

Do ∆⊥d => AB ⊥ d => AB→. u_d→ = 0

⇔ t+ t + 2(2t - 3) = 0 ⇔ 6t – 6= 0 nên t = 1

=> AB→(1; 1; -1)

Đường thẳng ∆ đi qua A và nhận AB^→ làm vectơ chỉ phương nên có phương trình

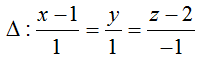
Chọn B.

Ví dụ 4: Cho đường thẳng ∆ có phương trình chính tắc 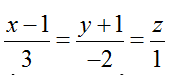; điểm A(-1;2; 0) . Đường thẳng d đi qua điểm A đồng thời vuông góc và cắt đường thẳng ∆ tại điểm có tọa độ là?

A. (-11/7; 5/7; -6/7)    B. (11/7; 5/7; -6/7)     C. (3/7; 5/7; 6/7)     D. (1/7; 5/7; -6/7)

Hướng dẫn giải:

+ Ta có đường thẳng ∆ có vecto chỉ phương u_∆→(3; -2;1)

Gọi giao điểm của đường thẳng d và ∆ là B.

+ Vì B thuộc đường thẳng ∆ nên tọa độ B có dạng B( 1+3t; -1-2t; t)

=> AB→( 2+ 3t; - 3- 2t; t)

+ Do ∆⊥d => ∆⊥AB => AB→.u_∆→ = 0

⇔ 3( 2+ 3t) – 2( - 3 -2t) + 1. t= 0

⇔ 6+ 9t + 6 + 4t + t= 0

⇔ 14t+ 12= 0 ⇔ t = -6/7

=> Tọa độ giao điểm của d và ∆ là B(11/7; 5/7; -6/7)

Chọn A.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho điểm M( 1;1;1) và đường thẳng d đi qua hai điểm A(1; 2;0) và B(-1;3;3). Gọi ∆ là đưởng thẳng qua M vuông góc và cắt d. Biết rằng đường thẳng d và ∆ cắt nhau tại N(-5/7;a/7;b/7) . Tính a+ b ?

A. 16    B. – 10     C. 18     D. -8

Hướng dẫn giải:

+ Đường thẳng d đi qua hai điểm A( 1;2;0) và B( -1; 3;3) nên đường thẳng này nhận vecto ( -2;1;3) làm vecto chỉ phương

=> Phương trình đường thẳng d

+ Gọi N là giao điểm của ∆ và d.

Do N thuộc đường thẳng d nên tọa độ N( 1- 2t; 2+ t; 3t)

=> MN→( - 2t; 1+ t; 3t – 1)

+ Do ∆⊥d => ∆⊥MN => AB→.MN→ = 0

⇔ - 2. (-2t) + 1. ( 1+ t) + 3( 3t-1) = 0

⇔ 4t+ 1+ t+ 9t – 3 = 0⇔ 14t - 2= 0 ⇔ t= 1/7

=> Tọa độ điểm N (-5/7; 15/7;3/7)

=> a= 15 và b = 3 nên a+ b= 18

Chon C.

Dạng 10: Viết phương trình đường thẳng d nằm trong mp (P) đồng thời cắt cả hai đường thẳng d₁ và d₂.

1. Phương pháp giải

- Tìm giao điểm A = d₁ ∩(P); B = d₂ ∩ (P)

- d là đường thẳng đi qua 2 điểm A và B

2. Ví dụ minh họa

Ví dụ 1: Viết phương trình của đường thẳng d nằm trong mặt phẳng (P): x – y – 2z + 3 = 0 và cắt hai đường thẳng

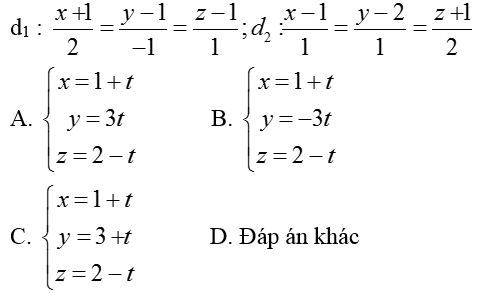
Hướng dẫn giải:

- Giao điểm A của d₁ và (P) có tọa độ ( 2t – 1; - t+ 1; t + 1)

Thay tọa độ A vào phương trình (P) có:

( 2t – 1) – ( - t+1) – 2(t+1)+ 3 = 0 ⇔ 2t – 1 + t- 1- 2t – 2 + 3 = 0

⇔ t - 1= 0 nên t=1 => A (1; 0; 2)

- Giao điểm B của d₂ và (P) có tọa độ ( t+ 1; t+2; 2t – 1)

Thay tọa độ điểm B vào phương trình (P) có:

( t+ 1) – ( t+ 2) – 2 (2t – 1) + 3= 0 ⇔ - 4t + 4= 0 nên t = 1

=> B (2; 3; 1)

-Ta có AB→(1; 3; -1)

Vậy phương trình của d là

Chọn A

Ví dụ 2: Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng 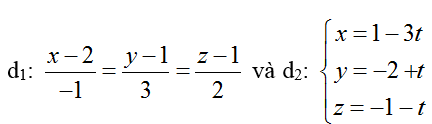. Đường thẳng d nằm trong (P): x+2y- 3z – 2= 0 và cắt hai đường thẳng d₁; d₂ lần lượt tại A và B. Tính AB?

A. 8    B. √35     C. √23     D. √59

Hướng dẫn giải:

+ Gọi A là giao điểm của d₁ và (P)

Tọa độ A( 2- t; 1+ 3t; 1+ 2t). Thay tọa độ điểm A vào phương trình (P) ta được:

2- t + 2( 1+ 3t) – 3( 1+ 2t) = 0

⇔ 2- t + 2+ 6t – 3 – 6t= 0

⇔ - t + 1= 0 ⇔ t= 1 nên A( 1; 4; 3)

+ Gọi B là giao điểm của d₂ và( P)

Tọa độ B( 1-3t; - 2+ t; - 1- t). Thay tọa độ điểm B vào phương trình (P) ta được:

1- 3t + 2( - 2+ t) – 3( - 1- t) - 2 = 0

⇔ 1- 3t – 4 + 2t + 3+ 3t – 2= 0

⇔ 2t – 2= 0 ⇔ t = 1 nên B ( -2; - 1; -2)

=> Độ dài

Chọn D.

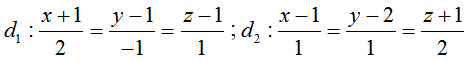
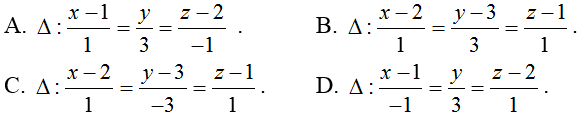
Ví dụ 3: Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng ; và mặt phẳng (P): x- y - 2z + 3= 0. Biết đường thẳng ∆ nằm trên mặt phẳng (P) và cắt hai đường thẳng d₁; d₂ . Phương trình ∆ là

Hướng dẫn giải:

Gọi A; B lần lượt là giao điểm của ∆ với d₁; d₂

Do Δ⊂(P)⇒A,B cũng chính là giao điểm của (P) với

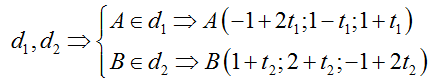
Khi đó :

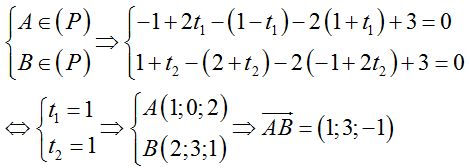
Suy ra phương trình

Chọn A.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho các điểm A( 1; 1;1); B(0;1; 2); C( 2; 1; 2). Viết phương trình đường thẳng d nằm trong mặt phẳng (P): x+ y- 2z- 3= 0 đồng thời cắt hai đường thẳng AB và OC?

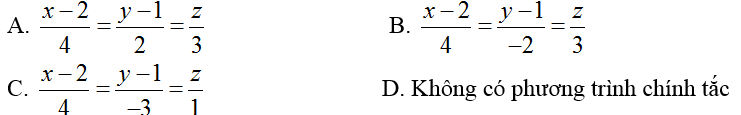
Hướng dẫn giải:

+ Phương trình đường thẳng AB: đi qua A( 1; 1; 1) vecto chỉ phương AB^→( -1; 0; 1)

=> Phương trình AB:

+ Gọi giao điểm của AB và mặt phẳng (P) là M( 1-t; 1; 1+ t) thay vào phương trình mặt phẳng (P) ta được:

1- t + 1- 2( 1+ t) – 3= 0 ⇔ 1- t + 1- 2- 2t- 3= 0

⇔ - 3t – 3= 0 ⇔ t= -1

Suy ra M( 2; 1; 0).

+ Phương trình đường thẳng OC : đi qua O(0; 0;0) và có VTCP OC^→(2; 1; 2) nên phương trình OC là:

+ Gọi giao điểm của OC và (P) là N( 2t; t; 2t) thay vào phương trình (P) ta được :

2t + t – 2.2t – 3= 0 ⇔ - t- 3= 0

⇔ t= - 3 nên N( -6; -3; - 6)

+ Đường thẳng d cần tìm chính là đường thẳng MN đi qua M( 2; 1; 0) và nhận vecto NM^→( 8; 4; 6) = 2( 4; 2; 3) làm vecto chỉ phương

=> Phương trình đường thẳng d là

Chọn A.

Viết phương trình đường thẳng d song song với d’ đồng thời cắt cả hai đường thẳng d₁ và d₂

1. Phương pháp giải

Cách 1:

- Viết phương trình mặt phẳng (P) song song với d’ và chứa d₁

- Viết phương trinh mặt phẳng (Q) song song với d’ và chứa d₂

- Đường thẳng cần tìm d = (P) ∩ (Q)

Cách 2:

M = d ∩ d₁; N = d ∩ d₂

Vì d // d’ nên MN^→ và u_d→ cùng phương hay MN^→ = k.u_d^→

2. Ví dụ minh họa

Ví dụ 1: Viết phương trình của đường thẳng d cắt hai đường thẳng d₁, d₂ và song song với d₃ biết

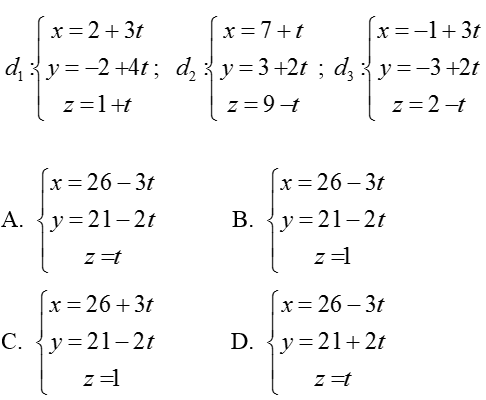
Hướng dẫn giải:

+ Vecto chỉ phương của ba đường thẳng d₁; d₂ và d₃ lần lượt là

u₁→ ( 3; 4; 1) ; u₂→ (1; 2; -1); u₃→ (3; 2; -1)

- Mặt phẳng (P) chứa d₁ và song song với d₃

Ta có vectơ pháp tuyến của (P) là n_P→ = [u₁→; u₃→] =( - 6; 6; -6)

Hay chọn 1 vectơ pháp tuyến của (P) là n→(1; -1; 1)

Một điểm thuộc d₁ là điểm thuộc (P) là : (2; -2; 1)

Phương trình mặt phẳng (P) là:

1.(x – 2) – 1.(y + 2) + 1. (z – 1) = 0 hay x – y + z – 5 = 0

- Mặt phẳng (Q) chứa d₂ và song song với d₃

Ta có vectơ pháp tuyến của (Q) là n_Q→ = [u₂→; u₃→] = ( 0 ; -2; -4)

Hay chọn 1 vectơ pháp tuyến của (Q) là n→(0; 1; 2)

Một điểm thuộc d₂ là điểm thuộc (Q) là : (7; 3; 9)

Phương trình mặt phẳng (Q) là:

0.(x – 7) + 1.(y – 3) + 2. (z – 9) = 0 hay y + 2z – 21 = 0

- Đường thẳng cần tìm d = (P) ∩ (Q) nên

Điểm M (x; y; z) ∈ d khi tọa độ của M là nghiệm của hệ phương trình:

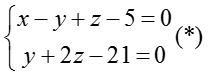
Đặt z = t, ta có:

Vậy phương trình tham số của d là:

Chọn A.

Ví dụ 2: Viết phương trình đường thẳng d song song với trục Ox và cắt hai đường thẳng

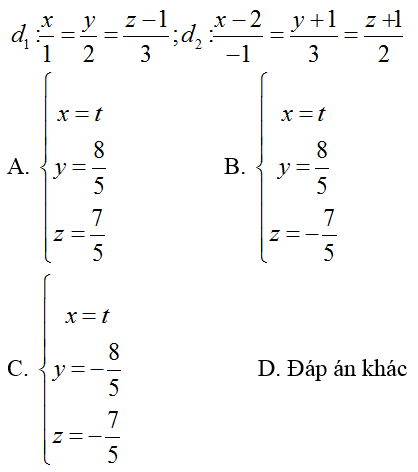
Hướng dẫn giải:

+ Đường thẳng d₁ và d₂ có vecto chỉ phương là u₁→(1; 2; 3); u₂→(- 1; 3; 2)

Trục Ox có vecto chi phương u_Ox→ (1; 0; 0)

- Mặt phẳng (P) chứa d₁ và song song với Ox

Ta có vectơ pháp tuyến của (P) là = (0; 3; -2)

Một điểm thuộc d₁ là điểm thuộc (P) là : (0; 0; 1)

Phương trình mặt phẳng (P) là:

0.(x – 0) + 3.(y – 0) – 2 . (z – 1) = 0 hay 3y – 2z + 2 = 0

- Mặt phẳng (Q) chứa d₂ và song song với Ox

Ta có vectơ pháp tuyến của (Q) là n_Q→ = [u₂→; u_Ox→] = (0; 2; -3)

Một điểm thuộc d₂ là 1 điểm thuộc (Q) là : (2; -1; -1)

Phương trình mặt phẳng (Q) là:

0.(x – 2) + 2.(y + 1) – 3 . (z + 1) = 0 hay 2y – 3z – 1 = 0

- Đường thẳng cần tìm d = (P) ∩ (Q) nên

Điểm M (x; y; z) ∈ d khi tọa độ của M là nghiệm của hệ phương trình:

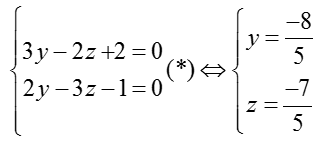
Vậy phương trình tham số của d là:

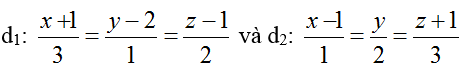
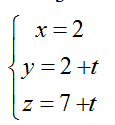
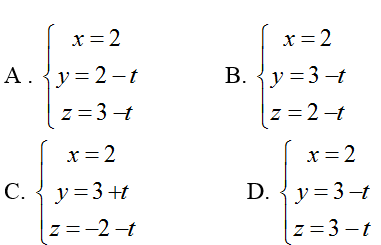
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng d₁: . Phương trình đường thẳng song song với d: và cắt hai đường thẳng d₁; d₂ là:

Hướng dẫn giải:

Gọi ∆ là đường thẳng cần tìm

Gọi giao điểm của ∆ với d₁ và d₂ lần lượt là A và B.

Do A thuộc d₁ nên tọa độ A (- 1+ 3a; 2+ a; 1+ 2a)

Do B thuộc d₂ nên tọa độ B ( 1+ b; 2b; - 1+ 3b)

Vecto AB→( b- 3a + 2; 2b- a- 2; 3b- 2a- 2) là một vecto chỉ phương của ∆.

+ Đường thẳng d có vectơ chỉ phương u_d→( 0; 1; 1) .

+ Do đường thẳng d//∆ nên haii vecto AB→; u_d→ cùng phương

=> có một số k thỏa mãn AB→= k.u_d→

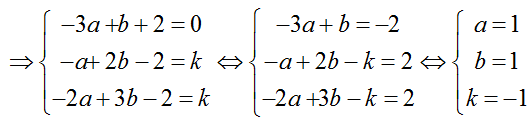
=> Tọa độ A( 2; 3; 3) và B(2; 2; 2)

+ Đường thẳng ∆ đi qua điểm A( 2; 3; 3) và có vectơ chỉ phương AB→(0; -1; -1)

Vậy phương trình của ∆ là

Chọn D.

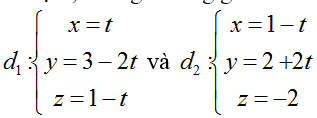
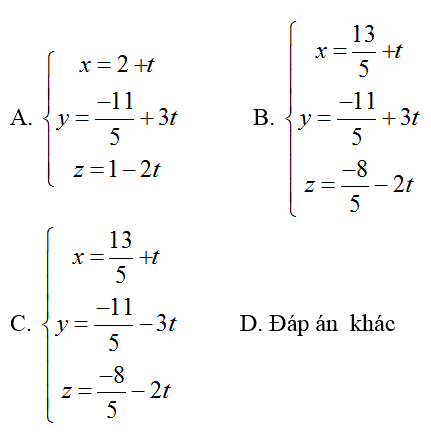
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng . Cho hai điểm M( 1;1;1 ) và N(0; -2 ; 3). Viết phương trình đường thẳng d cắt hai đường thẳng d₁ và d₂; song song với đường thẳng MN.

Hướng dẫn giải:

+ Gọi giao điểm của đường thẳng d với 2 đường thẳng d₁ và d₂ lần lượt là A và B.

+ Điểm A thuộc d₁ nên A( a; 3- 2a; 1- a)

+ Điểm B thuộc d₂ nên B( 1- b;2+ 2b; - 2) .

=> Vectơ AB→( 1- b- a; 2b+ 2a- 1; a- 3) là một vecto chỉ phươn của đường thẳng d

+ Đường thẳng MN nhận vecto MN→( -1; - 3; 2) làm vecto chỉ phương

+ Do đường thẳng d// MN nên 1 vecto chỉ phương của đường thẳng d là ( -1; - 3; 2)

=> Hai vecto AB→, MN→ cùng phương nên tồn tại số thực k khác 0 sao cho: AB^→ = k.MN^→

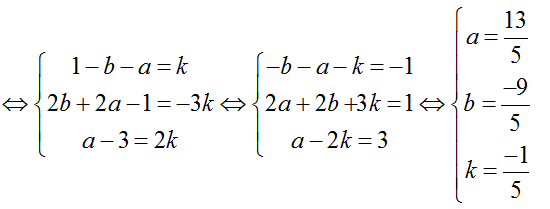
=> Tọa độ của A (13/5; -11/5; -8/5); B (14/5; -8/5; -2)

Đường thẳng d đi qua A và nhận vecto AB→(1/5; 3/5; -2/5) = 1/5(1;3-2) làm vecto chỉ phương

=> Phương trình đường thẳng d:

Chọn B

Dạng 12. Viết phương trình đường thẳng d là đường vuông góc chung của hai đường thẳng d₁ và d₂ chéo nhau.

1. Phương pháp giải

Cách 1:

- Viết PT mặt phẳng (P) chứa d₁ và song song với d₂

- Viết PT mặt phẳng (Q) chứa d₁ và vuông góc với (P)

- Tìm giao điểm M = d₁ ∩ (Q), pt đường thẳng vuông góc chung là đường thẳng đi qua M và vuông góc với (P)

Cách 2:

Gọi M = d ∩ d₁; N = d ∩ d₂

Vì d là đường vuông góc chung nên

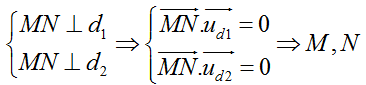
2. Ví dụ minh họa

Ví dụ 1: Viết phương trình đường vuông góc chung của hai đường thẳng chéo nhau sau:

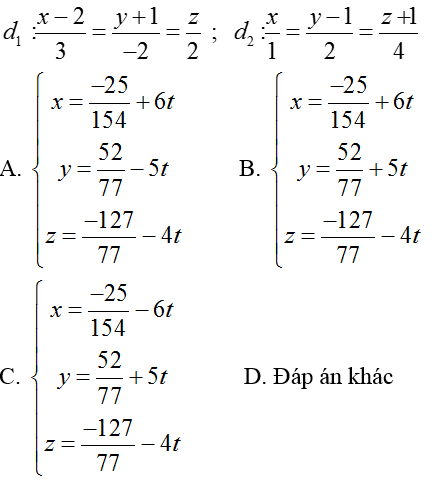
Hướng dẫn giải:

- Mặt phẳng (P) chứa d₁ và song song với d₂ có n_P→ = [u₁→; u₂→]= (-12; -10; 8)

Chọn 1 vectơ pháp tuyến của (P) là (6; 5; -4)

- Mặt phẳng (Q) chứa d₁ và vuông góc với (P) có n_Q→ = [u₁→; n_P→] = ( -2; 24; 27)

Một điểm thuộc d₁ cũng thuộc (Q) là: (2; -1; 0)

Phương trình mặt phẳng (Q) là:

– 2.(x – 2) + 24.(y + 1) + 27.(z – 0) = 0 hay – 2x + 24y + 27z + 28 = 0

- Giao điểm M = d₂ ∩ (Q) có tọa độ là (t; 2t + 1; 4t – 1) thỏa mãn:

– 2.t + 24(2t + 1) + 27(4t – 1) + 28 = 0 => t = -25/154

=> M(-25/154; 52/77; -127/77)

Đường thẳng vuông góc chung là đường thẳng d đi qua M và vuông góc với (P) nên có vectơ chỉ phương là vectơ pháp tuyến của (P) : (6; 5; -4)

Vậy phương trình đường thẳng cần tìm là:

Chọn B.

Ví dụ 2: Viết phương trình đường vuông góc chung của hai đường thẳng chéo nhau sau:

Hướng dẫn giải:

Gọi d là đường vuông góc chung của hai đường thẳng chéo nhau đã cho

M = d ∩ d₁ => M (t; 5-2t; 14-3t)

N = d ∩ d₂ => N (9-4t’; 3+t’; -1+5t’)

=> MN^→( 9- 4t’ – t; - 2+ t’+ 2t; -15 + 5t’ + 3t)

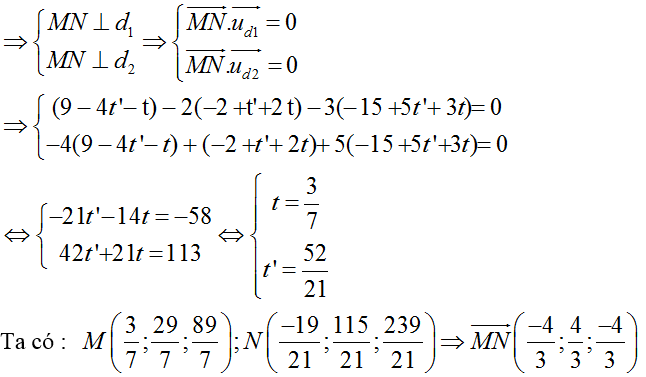
Ta có :

Chọn 1 vectơ chỉ phương của đường vuông góc chung d là (1; -1; 1)

Vậy phương trình của d là:

Chọn A.

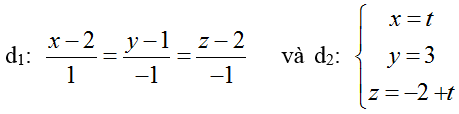
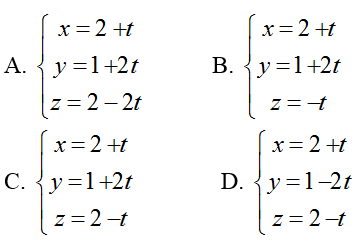
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng . Phương trình đường vuông góc chung của hai đường thẳng d₁; d₂ là.

Hướng dẫn giải:

Gọi d là đường thẳng cần tìm

Gọi A = d ∩ d₁; B = d ∩ d₂

+ Do A thuộc d₁ nên A( 2+a; 1- a; 2-a)

+ Do B thuộc d₂ nên B( b; 3; - 2+ b)

AB^→( - a+ b – 2; a + 2; a+ b - 4)

+ Đường thẳng d₁ có vectơ chỉ phương u₁→( 1; -1; -1)

+ Đường thẳng d₂ có vectơ chỉ phương u₂→(1; 0; 1)

+ Ta có:

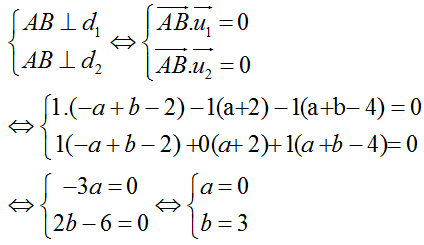
=> A( 2; 1; 2) và B( 3; 3; 1)

+ Đường thẳng d đi qua điểm A ( 2; 1; 2) và có vectơ chỉ phương AB^→( 1; 2; -1)

Vậy phương trình của d là

Chọn C.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho A( -1;1;0); B( 1;3;3); C( 1; 2; 1) và D( 1; 1; 1). Đường thẳng d là đường vuông góc chung của AC và BD cắt AC và BD lần lượt tại M và N. Tìm M?

A. ( -3; 0; -1)    B. ( 1; 0; 1)    C. ( -1; 0; 2)    D. Đáp án khác

Hướng dẫn giải:

+ Đường thẳng AC : Đi qua A( -1 ; 1 ; 0) và nhận vecto AC→( 2 ; 1 ;1) làm vecto chỉ phương nên có phương trình

+ Đường thẳng BD : đi qua B( 1 ; 3 ; 3) và nhận vecto BD→( 0 ; -2 ; -2) làm vecto chỉ phương nên có phương trình

+ M thuộc AC nên M( -1+ 2m;1+ m;m)

+ N thuộc BD nên N( 1; 3- 2n; 3- 2n)

=> MN→ ( 2+ 2m; 2-2n – m; 3- 2n- m)

+ Ta có đường thẳng MN vuông góc với AC và BD nên :

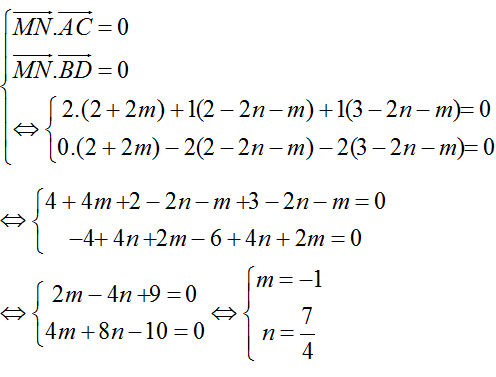
=> đường thẳng d cắt AC tại M( - 3; 0;-1)

Chọn A.

Dạng 13. Viết phương trình của đường thẳng d là hình chiếu của d’ trên mặt phẳng (P).

1. Phương pháp giải

1. Phương pháp giải

- Viết phương trình mặt phẳng (Q) chứa d’ và vuông góc với mặt phẳng (P)

- Hình chiếu cần tìm d = (P) ∩ (Q)

2. Ví dụ minh họa

Ví dụ 1: Viết phương trình đường thẳng d là hình chiếu của d’ trên (P) biết:

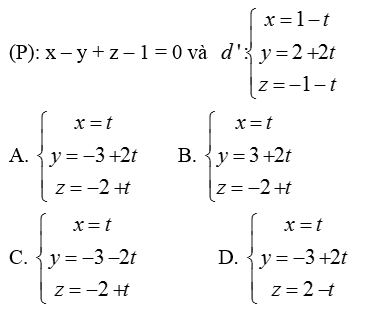
Hướng dẫn giải:

+ Đường thẳng d’ có vecto chỉ phương u_d'→( -1; 2; -1)

Mặt phẳng ( P) có vecto pháp tuyến là n_P→(1; -1; 1)

- Mặt phẳng (Q) chứa d’ và vuông góc với (P) có n_Q→ = [u_d'→;n_P→] = ( 1; 0; -1)

Một điểm thuộc d’ cũng thuộc (Q) là: (1; 2; -1)

Phương trình mặt phẳng (Q) là:

1.(x – 1) + 0.(y - 2) – 1.(z + 1) = 0 hay x – z – 2 = 0

- Hình chiếu cần tìm d = (P) ∩ (Q)

Tọa độ của điểm M (x; y; z) thuộc d thỏa mãn:

Chọn x = t

Vậy phương trình của d là

Chọn A.

Ví dụ 2: : Viết phương trình đường thẳng là hình chiếu của d trên (Oxy) biết

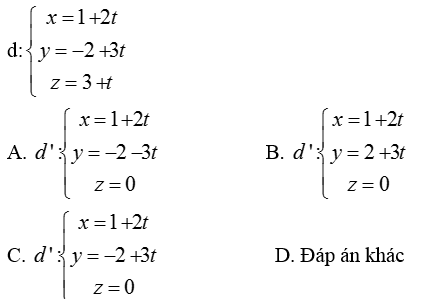
Hướng dẫn giải:

Mỗi điểm M (x; y; z) thuộc d có hình chiếu trên (Oxy) là điểm M’ (x; y; 0) thuộc d’ với d’ là hình chiếu của d trên (Oxy)

Vậy d’ có phương trình tham số là:

Chọn C.

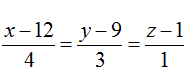
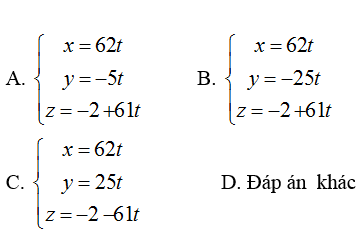
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng d: và mặt thẳng (P): 3x+ 5y – z- 2= 0 . Gọi d’ là hình chiếu của d lên (P). Phương trình tham số của d’ là

Hướng dẫn giải:

+ Gọi mặt phẳng (Q) chứa d và vuông góc với (P).

Đường thẳng d đi qua điểm B( 12; 9; 1) và có vectơ chỉ phương u_d→( 4; 3; 1).

Mặt phẳng (P) có vectơ pháp tuyến n_P→( 3; 5; -1)

=> Mặt phẳng (Q) qua B( 12; 9; 1) có vectơ pháp tuyến n→ = [u_d→; n_P→] = ( -8;7; 11)

=> Phuong trình (Q): - 8( x- 12) + 7( y- 9) + 11(z- 1) = 0

Hay – 8x + 7y + 11z + 22= 0

+ Đường thẳng d’ cần tìm là giao tuyến của (P) và (Q).

Tìm một điểm thuộc d’, bằng cách cho y= 0

Ta có hệ

=> M( 0; 0; - 2)

+ Đường thẳng d’ đi qua điểm M( 0; 0; - 2) và có VTCP u_d→= [n_P→; n_Q→] = ( 62; -25; 61)

Vậy phương trình tham số của d’ là:

Chọn B.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho hai điểm A(1; 1; -2) và B(0; 2; -2). Cho mặt phẳng ( P): x+ y- 2z- 6= 0. Viết phương trình đường thẳng d là hình chiếu của đường thẳng AB lên mặt phẳng ( P)?

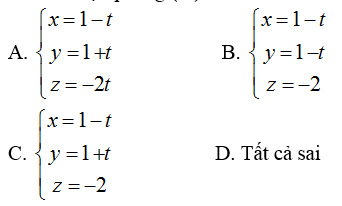
Hướng dẫn giải:

+ Thay tọa độ điểm A và B vào phương trình mặt phẳng ( P) ta được :

1+ 1- 2.(-2) – 6 = 0 ( thỏa mãn).

Và 0+ 2- 2( -2) – 6= 0 ( thỏa mãn) .

=> Hai điểm A và B cùng thuộc mặt phẳng (P).

Suy ra; mặt phẳng (P) chứa đường thẳng AB.

=> Hình chiếu của đường thẳng AB lên mặt phẳng (P) là chính nó.

+ Đường thẳng AB: đi qua A( 1; 1; -2) và nhận vecto AB→( -1; 1; 0)

=> Phương trình AB:

Chọn C.

Dạng 14. Vị trí tương đối của hai đường thẳng

1. Phương pháp giải

Vị trí tương đối giữa đường thẳng d (đi qua M_o và có vectơ chỉ phương u→) và đường thẳng d’ (đi qua M_o' và có vectơ chỉ phương u'→)

- d và d’ cùng nằm trong một mặt phẳng ⇔ [u→; u'→].M_oM'_o→ = 0

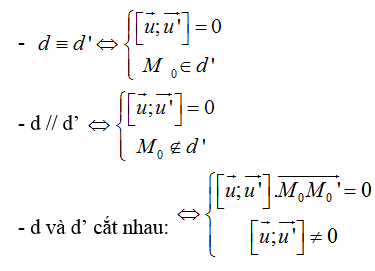
- d và d’ chéo nhau [u→; u'→].M_oM'_o→ ≠ 0

- d ⊥ d' ⇔ u→.u'→ = 0

2. Ví dụ minh họa

Ví dụ 1: Xét vị trí tương đối của các cặp đường thẳng d và d’:

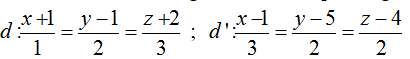
A. Song song    B. Trùng nhau     C. Cắt nhau    D. Chéo nhau

Hướng dẫn giải:

Đường thẳng d có u_d→(1; 2; 3) và đi qua M_o ( -1; 1; -2)

Đường thẳng d’ có u'_d→(3; 2; 2) và đi qua M_o' ( 1; 5; 4)

=> M_oM_o'^→ (2; 4; 6) và [u_d→;u'_d→] = (-2; 7; - 4) ≠ 0^→

Ta có: [u_d→;u'_d→].M_oM'_o→ = -2. 2+ 7.4 - 4.6 = 0

Vậy d và d’ cắt nhau..

Chọn C.

Ví dụ 2: Xác định vị trí tương đối của hai đường thẳng

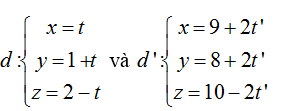
A. Cắt nhau    B. Trùng nhau    C. Chéo nhau    D. Song song

Hướng dẫn giải:

Đường thẳng d có vecto chỉ phương u_d→(1; 1; -1) và đi qua M_o (0; 1; 2)

Đường thẳng d’ có vecto chỉ phương u'_d→(2; 2; -2)

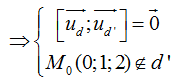
Nên hai đường thẳng d và d’ song song.

Chọn D.

Ví dụ 3: Tìm a để hai đường thẳng sau đây song song:

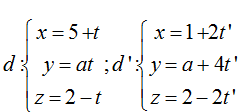
A. a= 2    B. a= -3    C. a= -2    D. a= 4

Hướng dẫn giải:

Đường thẳng d và d’ có vecto chỉ phương lần lượt là ( 1; a; -1) và (2; 4; -2)

Để d // d’ thì 1/2 = a/4 = -1/-2 => a = 2

Khi đó đường thẳng d’ đi qua điểm N (1; 2; 2) và điểm N không thuộc d.

Vậy d // d’ khi và chỉ khi a = 2

Chọn A.

Ví dụ 4: Xét vị trí tương đối của d và d’ biết 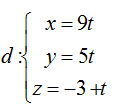và d’ là giao tuyến của hai mặt phẳng: (P) : 2x – 3y – 3z – 9 = 0 và (P’): x – 2y + z + 3 = 0

A. Trùng nhau     B.Song song    C. Cắt nhau    D. Chéo nhau

Hướng dẫn giải:

- Trước hết viết phương trình đường thẳng d’:

Lây điểm M’ (x; y; z) thuộc d’ có tọa độ thỏa mãn hệ:

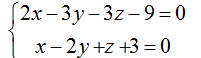
Chọn z = 0 ta được 1 điểm M’ thuộc d’ là (27; 15; 0)

Vectơ chỉ phương của d’ là u_d'→ = [n_P→; n_P'→] = ( -9; -5; -1)

- đường thẳng d có vecto chỉ phương u_d→( 9; 5; 1) => [u_d→;u_d'→] = 0^→ (1)

Lại có: M' ∈ d (2)

Từ (1) và (2) suy ra, d ≡ d’

Chọn A.

Ví dụ 5: Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng d₁: 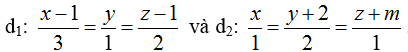. Khi đó, giá trị của m bằng bao nhiêu thì d₁ cắt d₂?

A. m= 0    B. m= 1    C. m= -2    D.Đáp án khác

Hướng dẫn giải:

+ Đường thẳng d₁: đi qua A(1; 0; 1) và nhận vecto u₁→( 3; 1; 2) làm vecto chỉ phương

+ Đường thẳng d₂: đi qua B(0; -2; -m) và nhận vecto u₂→(1; 2; 1) làm vecto chỉ phương

=> [u₁→; u₂→] = (-3; -1; 5) và AB^→(-1; -2; - m- 1 )

+ Để hai đường thẳng d₁ và d₂ cắt nhau thì: [u₁→; u₂→]. AB→ = 0

⇔ - 3.( -1) – 1( - 2) + 5( - m- 1) =0

⇔ 3+ 2- 5m- 5= 0 ⇔ 5m= 0 ⇔ m= 0

Chọn A.

Dạng 15.Vị trí tương đối của đường thẳng và mặt phẳng

1. Phương pháp giải

Cho đường thẳng d đi qua M_o(x_o; y_o; z_o) và có vectơ chỉ phương (a; b;c) , cho mặt phẳng (P) có phương trình tổng quát là: Ax + By + Cz + D = 0

Gọi là vectơ pháp tuyến của (P). Để xét vị trí tương đối giữa đường thẳng d và mặt phẳng (P) ta có cách sau:

Cách 1:

Xét tích vô hướng n→.u→ và thay tọa độ điểm M_o vào phương trình của (P) để kiểm tra, ta có các

trường hợp sau:

- n→.u→ = 0 và M_o ∉ (P) nên d song song với (P)

- n→.u→ = 0 và M_o ∈ (P) thì d nằm trong mp(P)

- n→.u→ ≠ 0 thì d cắt (P)

- n→ = k.u→ thì d vuông góc với (P)

Cách 2:

Viết phương trình tham số của đường thẳng d:

Thay x, y, z ở phương trình tham số trên vào phương trình tổng quát của mặt phẳng (P):

Ax + By + Cz + D = 0 ta được:

A(x_o + at) + B.(y_o+ bt) + C. (z_o+ ct) + D = 0 hay mt + n = 0 ( 1)

Xét số nghiệm t của phương trình (1) ta có các trường hợp sau:

- (1) vô nghiệm ⇔ d song song với (P)

- (1) có một nghiệm t = t_o khi d cắt (P) tại điểm M_o( x_o+ a. t_o; y_o+ bt_o; z_o+ t_o. c)

- (1) có vô số nghiệm ⇔ d nằm trong (P)

- (A; B; C) = k (a; b; c) ⇔ d vuông góc với (P)

2. Ví dụ minh họa

Ví dụ 1: Xét vị trí tương đối của đường thẳng d: 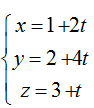với mặt phẳng (P): x + y + z + 2 = 0

A. Cắt nhau     B. (P) chứa d     C. Song song    D. Vuông góc

Hướng dẫn giải:

Đường thẳng d đi qua M_o(1; 2; 3) và có vectơ chỉ phương u→(2; 4; 1)

Mặt phẳng (P) có vectơ pháp tuyến là n→(1; 1; 1)

Ta có n→.u→ = 2.1+ 4.1+1.1 = 7

Vậy d cắt (P).

Chọn A.

Ví dụ 2: Xét vị trí tương đối của đường thẳng d: 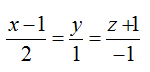với mặt phẳng (P): x+ 2z – 7 = 0?

A. Cắt nhau    B. Song song     C. (P) chứa d    D.Vuông góc

Hướng dẫn giải:

+ đường thẳng d đi qua điểm A( 1; 0; -1) và có vecto chỉ phương u→(2; 1; -1)

+ Mặt phẳng (P) c vecto pháp tuyến n→(1; 0; 2)

=> u→. n→ = 2. 1+ 0.1- 1.2= 0 và điểm A không thuộc mặt phẳng (P)

=> Đường thẳng d song song với mặt phẳng (P)

Chọn B.

Ví dụ 3: Trong không gian Oxyz, cho mặt phẳng (P): x- 2y+ 3z – 4= 0 và đường thẳng d: 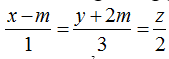. Với giá trị nào của m thì giao điểm của đường thẳng d và mặt phẳng (P) thuộc mặt phẳng (Oyz) .

A. m = 2    B. m= -1    C.m= 1    D.m= 3

Hướng dẫn giải:

Ta có: d ∩ (P) = A( x; y; z) .

A thuộc mặt phẳng (Oyz) nên x= 0 => A( 0; y;z)

Lại có; A thuộc ( P) nên: 0- 2y+ 3z- 4= 0

y = 3/2z - 2 nên A(0;3/2z -2 ;z)

+ Do A ∈ d nên:

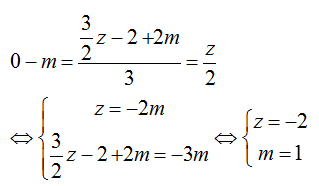
Chọn A.

Ví dụ 4: Trong không gian Oxyz, cho mặt phẳng (P): 2x+ my – 3z + m- 2= 0 và đường thẳng d: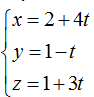 . Với giá trị nào của m thì d cắt (P)

A. m ≠ 1/2.    B. m= 1    C. m = 1/2 .    D. m ≠ -1

Hướng dẫn giải:

Mặt phẳng (P) có vecto pháp tuyến n→( 2; m; - 3)

Đường thẳng d có vecto chỉ phương u→( 4; -1;3)

Đường thẳng d cắt (P) ⇔ n→. u→ ≠ 0

⇔ 2. 4+ m.(- 1) – 3.3 ≠ 0 ⇔ -m-1 ≠ 0 ⇔ m ≠ -1

Chọn D

Ví dụ 5: Trong không gian Oxyz, cho đường thẳng d: 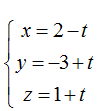và mặt phẳng (P): m²x- 2my + (6- 3m) z- 5= 0. Tìm m để d// (P)

Hướng dẫn giải:

Ta có đường thẳng d đi qua M( 2; -3; 1) và có vecto chỉ phương u→(-1; 1; 1)

Mặt phẳng (P) có vecto pháp tuyến n→( m2; -2m; 6- 3m)

Để d song song với (P) thì m²x- 2my + (6- 3m) z- 5= 0.

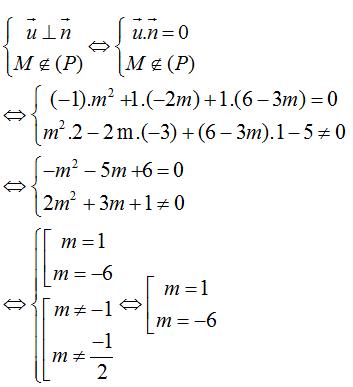
Chọn A.

Dạng 16.Vị trí tương đối của đường thẳng và mặt cầu

1. Phương pháp giải

Xét vị trí tương đối của đường thẳng d: 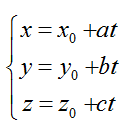và mặt cầu (S) tâm I(a’; b’; c’) bán kính R. Gọi d= d( I; d) thì:

d > R thì d không cắt (S).

d=R thì d tiếp xúc (S). Để tìm tọa độ giao điểm của đường thẳng và mặt cầu ( S) ta làm như sau:

Thay x= x_o+ at; y= y_o + bt; z= z_o + ct vào phương trình mặt cầu

=> t= .... => Tọa độ giao điểm.

d < R thì d cắt ( S) tại hai điểm A và B. Để tìm được tọa độ giao điểm ta làm như trên.

* Chú ý: đường thẳng d đí qua A và có vecto chỉ phương u→. Khi đó; khoảng cách từ điểm I đến đường thẳng d là:

2. Ví dụ minh họa

Ví dụ 1: Cho mặt cầu (S): x²+ y² + z²- 2x + 4z+ 1= 0 và đường thẳng d: 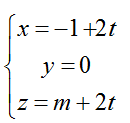. Biết có hai giá trị thực của tham số m để d cắt (S) tại hai điểm phân biệt A; B và các mặt phẳng tiếp diện của ( S) tại A và tại B luôn vuông góc với nhau . Tích của hai giá trị đó bằng

A. 16     B. 12    C.14    D. 10

Hướng dẫn giải:

+ Mặt cầu ( S) có tâm I( 1; 0; -2) và bán kính R= 2

Đường thẳng d qua M(- 1; 0; m) và vtcp u→( 2;0; 2)

+ Đường thẳng d cắt mặt cầu tại hai điểm phân biệt A và B nên IA= IB = R= 2.

Lại có các mặt phẳng tiếp diện của (S) tại A và B vuông góc với nhau nên IA vuông IB.

> Tam giác IAB vuông cân tại I.

Suy ra d( I; d)= IA.cos45^o = 2.√2/2 = √2

+ Mà IM→(-2; 0; m+ 2); [IM→; u→] =(0; 2m+ 8; 0)

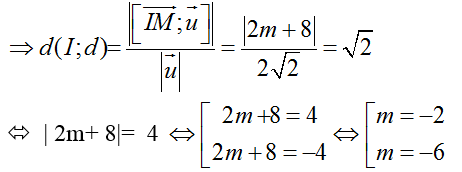
Suy ra m= -2 hoặc m= - 6 và tích cần tìm là ( -2). ( - 6) = 12.

Chọn B.

Ví dụ 2: Trong không gian Oxyz, cho đường thẳng 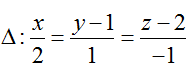và và mặt cầu ( S): x²+ y² + z² – 2x+ 4z + 1= 0. Số điểm chung của Δ và ( S) là

A.0    B.1    C.2.    D. 3

Hướng dẫn giải:

Đường thẳng Δ đi qua M( 0; 1; 2) và có VTCP u→(2;1;-1)

Mặt cầu (S) có tâm I (1; 0; -2) và bán kính R= 2.

Ta có MI→(1;-1;-4) và [u→;MI→] = (-5;7;-3)

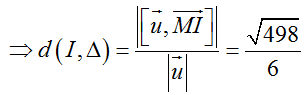
Vì d(I,Δ) > R nên Δ không cắt mặt cầu (S) .

Chọn A.

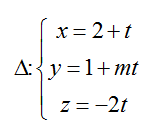
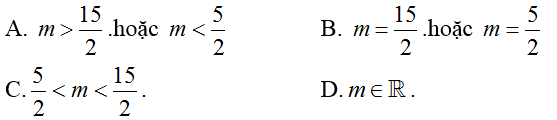
Ví dụ 3: Trong không gian Oxyz, cho đường thẳng và mặt cầu ( S): (x-1)²+ ( y+3)² + ( z- 2)²= 1. Giá trị của m để đường thẳng không cắt mặt cầu ( S) là:

Hướng dẫn giải:

Giao điểm nếu có của đường thẳng ∆ và mặt cầu (S) là nghiệm hệ phương trình :

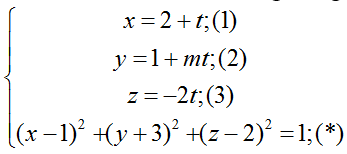
Thay (1); ( 2) và (3) vào ( *) ta được:

⇔ ( t+ 1)² + ( mt+ 4)²+ ( 2t+ 2)² = 1

⇔ t² + 2t+ 1+ m²t² + 8mt+ 16 + 4t² + 8t+ 4- 1= 0

⇔ (m² + 5)t² + 2( 5+ 4m)t+ 20 = 0 ( **)

Để ∆ không cắt mặt cầu ( S) thì (**) vô nghiệm, hay (**) có ∆’ < 0

⇔ ( 5+ 4m)² – 20( m² + 5) < 0

⇔ 25+ 40m+ 16m² – 20m² – 100 < 0

⇔ - 4m² + 40m – 75 < 0

⇔ m > 15/2 hoặc m < 5/2

Chọn A.

Ví dụ 4: Trong không gian Oxyz, cho mặt cầu ( S): x² +( y+1)² + (z- 1)² = 4 và đường thẳng d: 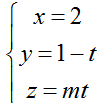. Giá trị của m để đường thẳng d cắt mặt cầu ( S) tại hai điểm phân biệt là:

A. m < 2 hoặc m > 5.    B. m > - 2 hoặc m - 5

C. m= 2 hoặc m = - 5    D. Không có giá trị nào của m thỏa mãn.

Hướng dẫn giải:

Giao điểm nếu có của đường thẳng d và mặt cầu ( S) là nghiệm hệ phương trình :

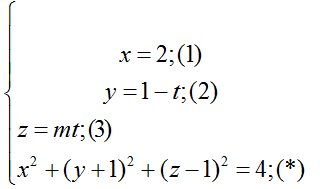
Thay (1); (2) ; (3) vào (*) ta được:

2² + ( 1- t+ 1)² + ( mt- 1)² =4

⇔ 4+ 4 – 4t+ t²+ t + m²t² - 2mt+ 1- 4= 0

⇔ ( m²+ 1)t² – ( 3+ 2m)t+ 5=0 ( **)

Để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt khi và chỉ khi phương trình (**) có hai nghiệm phân biệt

⇔ ∆ > 0 ⇔ ( 3+ 2m)² – 4. 5.( m² +1) > 0

⇔ 9+ 12m + 4m² – 20m² – 20 > 0

⇔ - 16m² + 12m- 11 > 0 ( vô lí - vì – 16m² + 12m- 11 < 0 với mọi m)

Chọn D.

Dạng 17. Hình chiếu của một điểm lên đường thẳng. Hình chiếu của một điểm lên mặt phẳng

1. Phương pháp giải

Cách xác định hình chiếu của 1 điểm A lên đường thẳng d

- Viết phương trình mặt phẳng (P) chứa điểm A và vuông góc với d

- Tìm H là giao điểm của d và (P) => H là giao điểm của A trên d

Cách xác định hình chiếu của 1 điểm A lên mặt phẳng (P)

- Viết phương trình đường thẳng đi qua A và vuông góc với (P)

- Tìm H là giao điểm của d và (P) => H là giao điểm của A trên (P)

2. Ví dụ minh họa

Ví dụ 1: Tìm hình chiếu vuông góc của A(1; 2; 1) trên đường thẳng d:

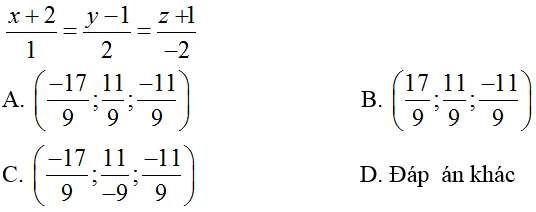
Hướng dẫn giải:

+ Đường thẳng d có vecto chi phương u→(1;2; -2).

+ Gọi mặt phẳng (P) chứa điểm A và vuông góc với d nhận vectơ chỉ phương của d làm vectơ pháp tuyến nên ta có phương trình của (P) là:

1(x – 1) + 2. (y – 2) – 2.(z – 1) = 0 hay x + 2y – 2z – 3 = 0

+ Tìm H là giao điểm của d và (P)

Tọa độ H( t – 2; 2t + 1; -2t – 1) thỏa mãn :

(t-2) + 2(2t+1) – 2(-2t-1) – 3 = 0 ⇔ 9t – 1= 0 ⇔ t = 1/9

Vậy H là hình chiếu của A trên d và H(-17/9; 11/9; -11/9)

Chọn A.

Ví dụ 2: Cho M(1; -1; 2) và mặt phẳng (P): 2x – y + 2z +2 = 0. Tìm tọa độ hình chiếu vuông góc H của M trên mặt phẳng (P)

A. ( 2; 1; 0)    B. ( - 2;0; 1)    C.(-1; 0; 0)    D. ( 0; 2; 1)

Hướng dẫn giải:

+ Mặt phẳng (P) có vecto pháp tuyến n→(2 ;- 1; 2).

Đường thẳng d đi qua M và vuông góc với (P) nhận vectơ pháp tuyến của (P) làm vectơ chỉ phương.

Suy ra phương trình của d là

+ Tìm H là giao điểm của d và (P)

Tọa độ của H(1+2t, -1-t; 2+2t) thỏa mãn:

2(1+2t) – (-1-t) + 2(2+2t) + 2 = 0

⇔ 2+ 4t + 1+ t + 4 + 4t + 2 = 0

⇔ 9t + 9= 0 ⇔ t = - 1 nên H ( - 1; 0; 0)

Chọn C.

Ví dụ 3: Cho điểm M (2; -1; 8) và đường thẳng d: 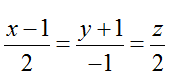.Tìm tọa độ H là hình chiếu vuông góc của điểm M trên d.

A. ( 1; 2; 1)     B.( 5; - 3; 4)     C. ( -2; 1;3)     D. ( 1;1;3)

Hướng dẫn giải:

Phương trình tham số của d là:

Xét điểm H(1+2t; -t-1; 2t) thuộc d => MH→( 2t – 1; - t; 2t – 8)

Đường thẳng d có vecto chỉ phương u_d→( 2; -1; 2)

H là hình chiếu vuông góc của M trên d khi và chỉ khi MH→.u_d→ = 0

⇔ 2(2t-1) – 1(-t) + 2(2t-8) = 0

⇔ 4t- 2+ t + 4t – 16 = 0

⇔ 9t – 18= 0 nên t= 2

=> Hình chiếu vuông góc của M lên d là H(5; - 3; 4)

Chọn B.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng d: 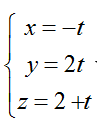và điểm M(1; 1; 1). Xác định điểm M’ đối xứng với M qua d?

A.( 1; 0; - 2)     B. ( -2; 1; 1)    C. ( 1; 2; 3)    D. (- 1; 0; 6)

Hướng dẫn giải:

+ Đường thẳng d đi qua A(0; 0; 2) và có vecto chỉ phương u→( -1; 2; 1)

+ Gọi (P) là mặt phẳng qua M và vuông góc với đường thẳng d nên mặt phẳng (P) nhận vecto chỉ phương của đường thẳng d làm vecto pháp tuyến

=> Phương trình mặt phẳng (P):

-1( x- 1) + 2( y-1) + 1( z- 1) = 0 hay – x + 2y + z – 2= 0

+ Gọi H là hình chiếu vuông góc của điểm M lên d khi đó H chính là giao điểm của đường thẳng d và mặt phẳng (P)

+ Điểm H thuộc đường thẳng d nên H(- t; 2t; 2+ t). Thay tọa độ H vào phương trình mặt phẳng (P) ta được:

- ( - t) + 2. 2t+ 2+ t- 2= 0 ⇔ 6t = 0 ⇔ t= 0

=> Hình chiếu của M lên d là H ( 0; 0; 2)

+ Do M’ đối xứng với M qua d nên H là trung điểm của MM’.

=> Tọa độ điểm M’( - 1; 0; 6 )

Chọn D.

Dạng 18.Khoảng cách từ một điểm đến đường thẳng. Khoảng cách giữa hai đường thẳng chéo nhau

1. Phương pháp giải

- Muốn tìm khoảng cách từ một điểm M đến đường thẳng d: có 2 cách sau:

+ Cách 1. Tìm hình chiếu H của điểm đó đến d => MH là khoảng cách từ A đến d

+ Cách 2. Công thức (với u^→ là vectơ chỉ phương của d và M_o là một điểm thuộc d)

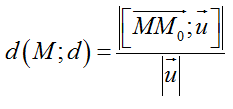
- Muốn tìm khoảng cách giữa hai đường thẳng chéo nhau d ( u→ là vectơ chỉ phương của d và d đi qua M_o) và d’ ( u'^→ là vectơ chỉ phương của d’ và d’ đi qua M'_o) ta làm như sau:

+ Viết phương trình mặt phẳng (P) chứa d và song song d’

+ Khoảng cách giữa d và d’ chính là khoảng cách từ điểm M'_o đến mặt phẳng (P)

d( d,d’) = d(M'_o; (P))

+ Hoặc dùng công thức:

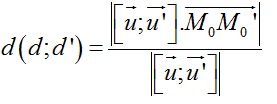
2. Ví dụ minh họa

Ví dụ 1: Tìm khoảng cách của A(-2; 1; 3) đến đường thẳng

A. 4√5/3    B. 5√5/2    C. 3√5    D.2√5

Hướng dẫn giải:

Đường thẳng d đi qua B( 0; 1; -1) và có vectơ chỉ phương u→( 1; 2; -2)

Ta có: AB^→(2; 0; -4); [AB→;u→] = ( 8;0; 4)

Vậy

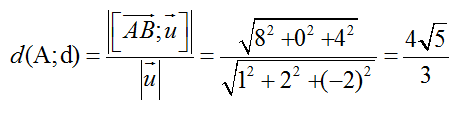
Chọn B.

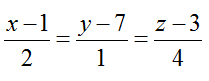
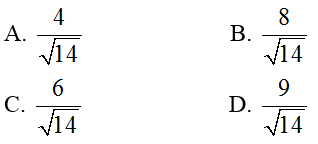
Ví dụ 2: Cho mặt phẳng (P): 3x – 2y – z + 5 = 0 và đường thẳng d: Tính khoảng cách giữa d và (P)

Hướng dẫn giải:

Mặt phẳng (P) có vecto pháp tuyến n_P→( 3; -2; -1)

Đường thẳng d có vecto chỉ phương u_d→(2; 1; 4) và đi qua điểm M_o (1; 7; 3)

Ta có: n_P→. u_d→ = 3.2 -2.1 – 1. 4 = 0 và M_o ∉ (1; 7; 3) (P)

Vậy d // (P)

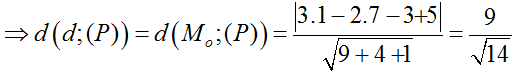
Chọn D.

Ví dụ 3: Tính khoảng cách giữa hai đường thẳng

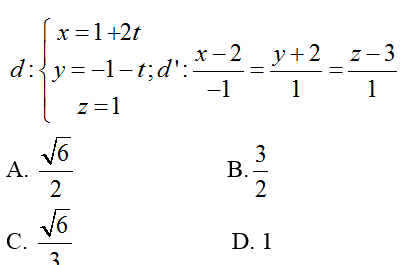
Hướng dẫn giải:

Đường thẳng d có vecto chỉ phương là u_d→( 2; -1; 0)

Đường thẳng d’ có vecto chỉ phương là u'_d→( -1; 1; 1).

- Gọi (P) là mặt phẳng chứa d và song song với d’. (P) nhận VTPT là n_P→ = [u_d→; u'_d→] = (-1;-2; 1)

Điểm M_o (1; -1; 1) thuộc d cũng thuộc (P) nên phương trình mặt phẳng (P) là:

- 1(x-1) – 2(y+1) + 1(z-1) = 0 hay x + 2y – z + 2 = 0

- d’ đi qua M'_o (2; -2; 3)

Vậy

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng 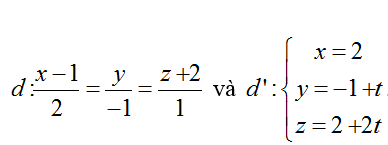. Xác định khoảng cách giữa hai đường thẳng đã cho?

Hướng dẫn giải:

+ Đường thẳng d đi qua A( 1;0; - 2) và có vecto chỉ phương u₁→( 2;-1; 1)

+ Đường thẳng d’ đi qua B( 2; -1; 2) và có vecto chỉ phương u₂→(0;1; 2)

=> AB→(1; -1; 4); [u₁→; u₂→] =( -3; -4; 2)

Khoảng cách giữa hai đường thẳng đã cho là:

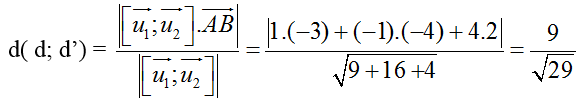
Chọn B.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho điểm A(-1; 0;2) và đường thẳng d: 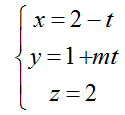. Tìm m để khoảng cách từ A đến d là √2 ?

A. m= -1 hoặc m = -2/3    B. m= - 1 hoặc m = 1/7

C. m = 1 hoặc m= - 1    D. m = 1 hoặc m = 1/7

Hướng dẫn giải:

+ Đường thẳng d đi qua M( 2; 1; 2) và có vecto chỉ phương u→(-1; m; 0)

+ Ta có: AM→(3; 1; 0) và [AM→; u→] = ( 0; 0; 3m+ 1)

+ Theo đầu bài ta có: d( A; d) = √2

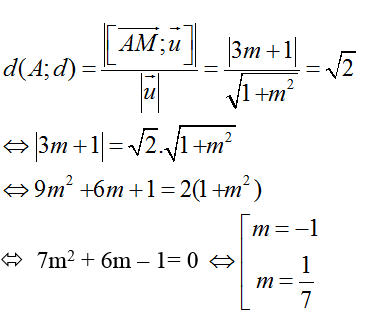
Chọn B.

Dạng 19. Góc giữa hai đường thẳng. Góc giữa đường thẳng và mặt phẳng

1. Phương pháp giải

- Cho hai đường thẳng d, d’ có vectơ chỉ phương u→(a; b; c) và u'→(a’; b’; c’)

Góc Φ giữa hai đường thẳng được tính theo công thức:

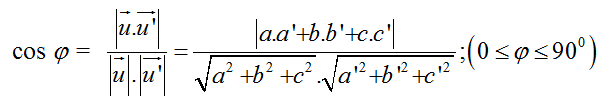
- Cho đường thẳng d có vectơ chỉ phương u^→(a,b,c) và mặt phẳng (P) có VTPT n→(A; B;C)

Góc φ giữa đường thẳng d và mặt phẳng (P) được tính theo công thức:

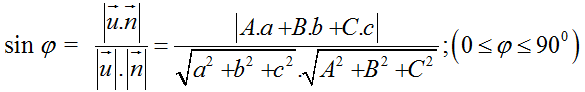
2. Ví dụ minh họa

Ví dụ 1: Tính góc giữa 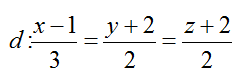và d’ là giao tuyến của hai mặt phẳng (P): x + 2y – z + 1 = 0 và (Q): 2x + 3z – 2 = 0?

A. 30^o     B. 45^o     C. 60^o     D. 90^o

Hướng dẫn giải:

Hai mặt phẳng (P) và (Q) có vecto pháp tuyến là n_P→(1; 2; -1) và n_Q→(2; 0; 3)

d' là giao tuyến của (P) và (Q) nên vectơ chỉ phương của d’ là u_d'→ = ( 6; -5; -4)

Đường thẳng d có vecto chỉ phương n→(3; 2;2)

Cosin góc giữa d và d’ là:

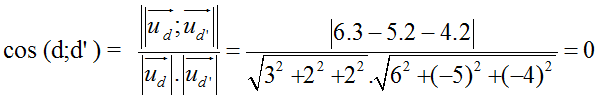
Suy ra, góc giữa d và d’ bằng 90^o.

Chọn D.

Ví dụ 2: Tính sin góc giữa đường thẳng d và mặt phẳng (P) biết d: 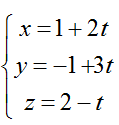và (P): 2x – y + 2z – 1 = 0?

A. √14/42     B. √14/22     C. √7/42    D. Đáp án khác

Hướng dẫn giải:

Đường thẳng d có vecto chỉ phương u_d→(2; 3; -1)

Mặt phẳng (P) có vecto pháp tuyến n_P→(2; -1; 2) nên sin góc giữa d và (P) là:

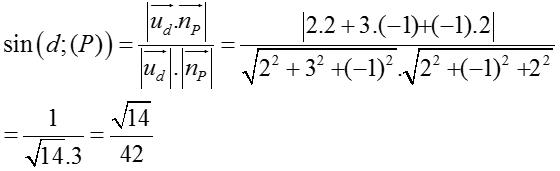
Chọn A.

Ví dụ 3: Cho bốn điểm A( 1; 0;1) ; B( -1; 2; 1); C( -1; 2; 1) và D( 0; 4; 2). Xác định cosin góc giữa hai đường thẳng AB và CD?

Hướng dẫn giải:

+ Đường thẳng AB có vecto chỉ phương AB→(-2;2;0)

+ Đường thẳng CD có vecto chỉ phương CD→(1;2;1).

=> Cosin góc giữa hai đường thẳng AB và CD là:

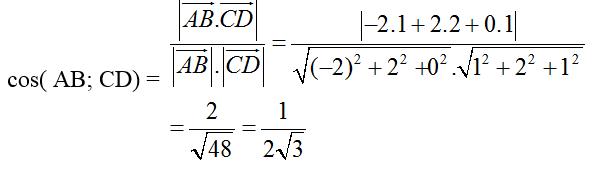
Chọn C.

Ví dụ 4: Cho đường thẳng 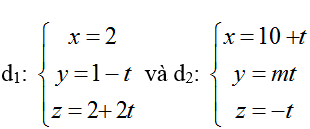. Xác định m để cosin góc giữa hai đường thẳng đã cho là √5/5

A. m = 2    B. m = - 4    C. m = -1/2    D. m = 1/4

Hướng dẫn giải:

Đường thẳng d₁ có vecto chỉ phương u₁→(0; - 1; 2)

Đường thẳng d₂ có vecto chỉ phương u₂→(1; m; -1)

Cosin góc tạo bởi hai đường thẳng đã cho là:

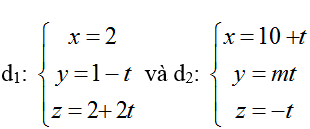
Để cosin góc giữa hai đường thẳng đã cho là

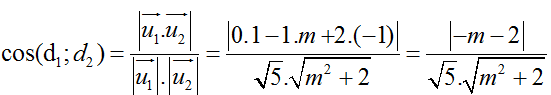
⇔ m² + 4m+ 4 = m² + 2 ⇔ 4m = - 2 ⇔ m =-1/2

Chọn C.

Ví dụ 5: Cho đường thẳng d: 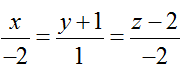và mặt phẳng (P): x+ my- z+ 100= 0. Xác định m để cosin góc giữa đường thẳng d và mặt phẳng (P) là 1/3√3 ?

A. m= ±1     B.m= ±2     C. m= 0     D. m = ±3

Hướng dẫn giải:

Đường thẳng d có vecto chỉ phương u→(-2; 1; - 2)

Mặt phẳng (P) có vecto pháp tuyến n→(1; m;-1)

Do đó, sin góc tạo bởi đường thẳng d và mặt phẳng (P) là:

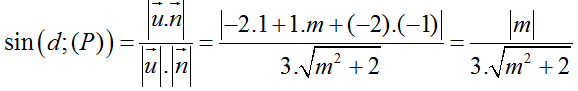
Theo giả thiết ta có:

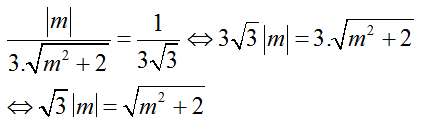
⇔ 3m²= m² + 2 ⇔ 2m² = 2 ⇔ m² = 1 ⇔ m= ±1

Chọn A.