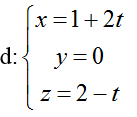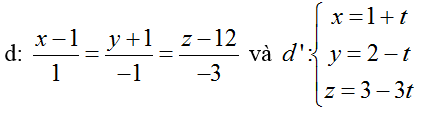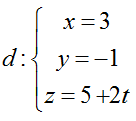21 dạng Viết phương trình mặt phẳng trong đề thi Đại học có lời giải - Toán lớp 12

---

21 dạng Viết phương trình mặt phẳng trong đề thi Đại học có lời giải

Với 21 dạng Viết phương trình mặt phẳng trong đề thi Đại học có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình mặt phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1: Viết phương trình mặt phẳng (P) đi qua điểm M và nhận vecto n→ làm vecto pháp tuyến

1. Phương pháp giải

+ Phương trình mặt phẳng đi qua điểm M(x_o; y_o; z_o) và có vecto pháp tuyến n→(A;B;C) ≠ 0^→ :

A.(x- x_o) + B( y- y_o)+C( z- z_o) =0

2. Ví dụ minh họa

Ví dụ 1: Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm A(0; 1; -1) và có vecto pháp tuyến n^→(2;3;4)

A. y – z + 1 = 0    B. 2x + y - z- 3= 0

C. 2x + 3y + 4z +1= 0    D. 2x- 3y - 4z - 1 = 0

Hướng dẫn giải:

Mặt phẳng (P) đi qua điểm A (0;1; -1) và có vecto pháp tuyến n→(2;3;4) có phương trình là:

2( x- 0) + 3( y – 1) + 4( z + 1) = 0

Hay 2x + 3y + 4z + 1 = 0

Chọn C.

Ví dụ 2: Cho hai điểm A( 1;2; 7) và B(3; 0; -3), gọi M là trung điểm của AB. Viết phương trình mặt phẳng đi qua điểm M và vecto pháp tuyến n^→(2;-3;1)

A. 2x - 3y+ z + 2 = 0    B. 2x - 3y + z + 3=0

C. 2x - 3y+ z = 0    D. 2x – 3y + z - 3= 0

Hướng dẫn giải:

+ Do M là trung điểm của AB nên tọa độ điểm M là:

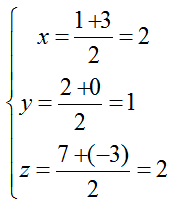
=> M(2; 1; 2)

+ Mặt phẳng đi qua điểm M( 2; 1; 2) và có vecto pháp tuyến có phương trình là:

2( x – 2) -3( y- 1)+ 1( z – 2 ) = 0

Hay 2x -3y + z - 3= 0

Chọn D.

Ví dụ 3: Cho tam giác ABC biết A( 2; 1; 3) và B( - 2; 3; -1) và C( 0; 2; 1), gọi G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng đi qua điểm G và vecto pháp tuyến n^→(2;1;1)

A. 2x+ y+ z- 3= 0    B. 2x+ y- z+ 3=0

C. 2x+ z- 3= 0    D. 2x+ y- z- 6= 0

Hướng dẫn giải:

+ Do G là trọng tâm của tam giác ABC nên tọa độ điểm G là:

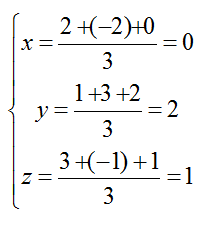
=> G( 0; 2; 1)

+ Mặt phẳng đi qua điểm G(0; 2; 1) và có vecto pháp tuyến n→(2;1;1) có phương trình là:

2( x- 0) + 1( y - 2) + 1.( z - 1) = 0

Hay 2x+ y+ z – 3= 0

Chọn A.

Viết phương trình mặt phẳng (α) đi qua điểm M (x_o; y_o; z_o) và song song với một mặt phẳng (P): Ax+ By + Cz + D= 0.

1. Phương pháp giải

Cách 1:

Vecto pháp tuyến của mặt phẳng (P) là: n^→(A;B;C)

Do mặt phẳng (α) // (P) nên vecto pháp tuyến của mặt phẳng (α) là n→(A;B;C)

Phương trình mặt phẳng (α):

A(x- x_o) + B. (y – y_o) + C( z- z_o) = 0

Cách 2:

Mặt phẳng (α ) // (P) nên phương trình mặt phẳng (α) có dạng:

Ax+ By + Cz + D’= 0 (*) với D' ≠ D

Vì mặt phẳng (α) đi qua điểm M (x_o; y_o; z_o) nên thay tọa độ điểm M vào (*) tìm đươc D’

2. Ví dụ minh họa

Ví dụ 1: Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M (-1; 2; 0) và song song với mặt phẳng (Q): x + 2y – 3z + 10 = 0.

A. x + 2y – 3z - 3= 0    B. x - 2y+ 3z + 5 = 0

C. x+ 2y - 3z +3 = 0    D. – x+ 2y + 10 = 0

Hướng dẫn giải:

Mặt phẳng (P) song song với mặt phẳng (Q) nên vecto pháp tuyến của mặt phẳng (P) là n→(1;2-3) .

Mặt phẳng (P) đi qua điểm M ( -1; 2; 0) và có vecto pháp tuyến n→(1;2-3) nên có phương trình:

1( x+1) + 2(y- 2) – 3( z- 0) = 0 hay x+ 2y – 3z – 3 = 0

Chọn A.

Ví dụ 2: Cho hai điểm A(0; -2;1) và B( 2; 0; 3). Gọi M là trung điểm của AB. Viết phương trình mặt phẳng (P) đi qua M và song song với mặt phẳng Q: 2x + 5y +z - 10 =0

A. 2x+ 5y + z+ 2= 0    B. 2x+ 5y + z+ 3= 0

C. 2x+ 5y + z - 4= 0    D. 2x+ 5y + z+ 1= 0

Hướng dẫn giải:

Do M là trung điểm của AB nên tọa độ điểm M là:

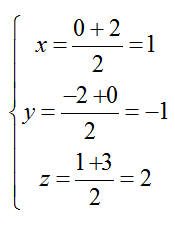
=> M( 1; -1; 2)

Do mặt phẳng (P) song song với mặt phẳng (Q) nên mặt phẳng (P) có vecto pháp tuyến n→(2;5;1)

Phương trình mặt phẳng (P) có vecto pháp tuyến n→(2;5;1) và đi qua điểm M (1; -1; 2) là:

2( x- 1) + 5( y+ 1) + 1(z- 2) = 0 hay 2x + 5y + z + 1= 0

Chọn D.

Ví dụ 3: Trong không gian Oxyz, cho các điểm A (5; 1; 3), B(1; 2; 6), C(5; 0; 4), D( -1; 2; -3). Viết phương trình mặt phẳng đi qua D và song song với mặt phẳng (ABC)

A. x+ y – z - 4= 0    B. x+ y +z+ 2= 0     C.x - y+ z+ 6= 0     D. Tất cả sai

Hướng dẫn giải:

Ta có:

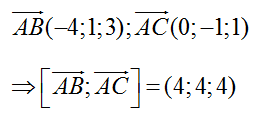
Gọi n→ là một vecto pháp tuyến của mặt phẳng (ABC) ta có 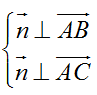nên n^→ cùng phương với [AB^→, AC^→]

Chọn n→(1;1;1) là vecto pháp tuyến của mặt phẳng (ABC)

Do mặt phẳng (P) song song với mặt phẳng (ABC) nên mặt phẳng (P) có vecto pháp tuyến n→(1;1;1)

Phương trình mặt phẳng (P) đi qua D (-1; 2; -3) và có vecto pháp tuyến n→(1;1;1) là:

1( x+ 1) + 1( y – 2) + 1( z+ 3) = 0 hay x+ y + z + 2= 0

Chọn C.

Ví dụ 4: Trong không gian Oxyz, cho các điểm A (-2;1;3), B(1; 2; 4), C(2; -1;3), D(0; 0; -1). Viết phương trình mặt phẳng đi qua D và song song với mặt phẳng (ABC)

A. x+ 2y+ z- 2= 0     B. x- 2y- 5z- 5= 0     C. x+ 2y- 5z- 9= 0     D. Tất cả sai

Hướng dẫn giải:

Ta có:

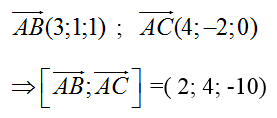
Gọi n→ là một VTPT của mặt phẳng (ABC) ta có 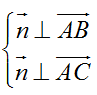nên n^→ cùng phương với

Chọn n→(1;2;-5) là vecto pháp tuyến của mặt phẳng (ABC)

Do mặt phẳng (P) song song với mặt phẳng (ABC) nên mặt phẳng (P) có VTPT n→ (1; 2; -5).

Phương trình mặt phẳng (P) đi qua D (0; 0; -1) và có vecto pháp tuyến n→ là:

1. (x – 0)+ 2( y – 0) - 5( z+ 1) =0 hay x+ 2y – 5z – 5 = 0

Chọn D.

Dạng 3: Viết phương trình mặt phẳng đi qua 3 điểm A, B, C không thẳng hàng. Viết phương trình mặt phẳng đi qua một điểm và nhận hai vecto u^→, v^→ làm vecto chỉ phương

1. Phương pháp giải

* Viết phương trình mặt phẳng đi qua 3 điểm A, B, C không thẳng hàng.

1. Tìm tọa độ các vecto AB→, AC→

2. Vecto pháp tuyến của mặt phẳng (P) là n→ = [AB→, AC→]

3. Điểm thuộc mặt phẳng: A (hoặc B, hoặc C)

4. Viết phương trình mặt phẳng đi qua 1 điểm và có vecto pháp tuyến n→ = [AB→, AC→]

Chú ý: Phương trình mặt phẳng (P) đi qua 3 điểm A(a;0;0); B(0;b;0); C(0;0;c) có dạng là:

x/a + y/b + z/c = 1 với a.b.c ≠ 0.

Trong đó A ∈ Ox; B ∈ Oy; C∈ Oz. Khi đó (P) được gọi là phương trình mặt phẳng theo đoạn chắn.

* Viết phương trình mặt phẳng đi qua một điểm M và nhận hai vecto u→, v→ làm vecto chỉ phương

1: Vecto pháp tuyến của mặt phẳng ( P): n→ = [u→, v→]

2. Mặt phẳng ( P) đi qua điểm M và nhận vecto n làm VTPT

=> Phương trình mặt phẳng (P).

2. Ví dụ minh họa

Ví dụ 1: Trong không gian Oxyz, viết phương trình mặt phẳng đi qua ba điểm A(1; -2; 0), B(1; 1; 1) và C(0; 1; -2)

A. 9x- 3y+ 3z- 11= 0    B. 9x+ y- 3z – 7= 0

C. 9x- y- 3z- 11=0    D. 9x- y+ 3z- 10= 0

Hướng dẫn giải:

Ta có: AB→(0;3;1); AC→ => [AB→, AC→]= ( - 9; -1; 3)

Gọi n→ là một vecto pháp tuyến của mặt phẳng (ABC) ta có 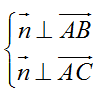nên n^→ cùng phương với [AB^→, AC^→]

Chọn n→( 9;1; -3) ta được phương trình mặt phẳng (ABC) là

9.( x – 1)+1.(y + 2) - 3( z - 0) = 0 hay 9x + y – 3z – 7 = 0

Chọn B.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M(5; 4; 3) và cắt các tia Ox, Oy, Oz tại các điểm A, B, C sao cho OA = OB = OC. Viết phương trình mặt phẳng (P).

A. x+ y+ z - 12 = 0    B. x- y- z + 2= 0

C. x- y+ z – 4= 0    D. x+ y- z – 6= 0

Hướng dẫn giải:

Do mặt phẳng (P) cắt các tia Ox, Oy, Oz tại các điểm A, B, C sao cho OA = OB = OC nên

A (a; 0; 0); B(0; a; 0); C(0; 0; a) ; ( a > 0)

Phương trình mặt phẳng (P) theo đoạn chắn là: x/a + y/a + z/a = 1

Do mặt phẳng (P) đi qua điểm M (5; 4; 3) nên ta có:

5/a + 4/a + 3/a = 1 => 12/a = 1 => a = 12

Khi đó, phương trình mặt phẳng (P) là: x/12 + y/12 + z/12 = 1 hay x+ y + z – 12 = 0

Chọn A.

Ví dụ 3: Trong không gian hệ tọa độ Oxyz, cho bốn điểm A(5; 1; 3), B(1; 6;2), C(5; 0; 4), D(4; 0; 6). Mặt phẳng (P) đi qua hai điểm A, B và song song với đường thẳng CD có phương trình là:

A. x+ 4y+ z- 27= 0    B. 10x+ 9y+ 5z- 74= 0

C. 10x- 5y- 9z+ 22= 0    D. Tất cả sai

Hướng dẫn giải:

Ta có: AB→(-4;5-1); CD→(-1;0;-2) => [AB→, CD→] = (10; 9; 5)

Gọi n^→ là một vecto pháp tuyến của mặt phẳng (P)

Do A, B thuộc mặt phẳng (P), mặt phẳng (P) song song với đường thẳng CD nên ta có: 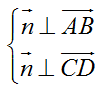nên n^→ cùng phương với [AB^→, CD^→].

Chọn n→ = (10;9;5)

Vậy phương trình mặt phẳng (P) có vecto pháp tuyến n^→ và đi qua điểm A(5; 1; 3) là:

10 (x – 5) + 9 ( y- 1) + 5 ( z – 3) = 0 hay 10x + 9y + 5z – 74 = 0

Chọn B.

Ví dụ 4: Viết phương trình mặt phẳng (P) đi qua M( 2; -1; 2)và nhận hai vecto u→(1;2;3) và v→(-2;1;0) làm vecto chỉ phương?

A. 3x+ 6y- 5z+ 1= 0    B. – 3x- 6y + 5z- 10= 0

C. 3x+ 5y- 6x+ 8= 0    D. 3x- 6y+ 5z+ 1= 0

Hướng dẫn giải:

Ta có hai vecto u→(1;2;3) và v→(-2;1;0) là vecto chỉ phương của mặt phẳng (P) nên một vecto pháp tuyến của mp (P) là: n^→ = [u^→,v^→] = (- 3; - 6; 5)

Mặt phẳng (P) nhận n→ làm vecto pháp tuyến và đi qua điểm M( 2; -1; 2 ) nên phương trình mặt phẳng ( P) là:

-3( x- 2) – 6 ( y+ 1) + 5( z-2)= 0 hay – 3x- 6y+ 5z - 10= 0

Chọn B.

Ví dụ 5: Viết phương trình mặt phẳng (P) đi qua A( 2; -3; 4); B(2; 1; -3) và mặt phẳng (P) nhận vecto u→( 2; 0; 1) làm vecto chỉ phương ?

A. 2x- 7y- 4z- 9= 0    B. 2x- 5y+ 3z – 9= 0

C. 2x+ 5y- 7z+ 10= 0    D. 2x+ 7y- 4z+ 10= 0

Hướng dẫn giải:

+ Ta có: AB^→(0; 4; -7)

+ Lại có mặt phẳng ( P) nhận vecto u→( 2; 0; 1) làm vecto chỉ phương nên một vecto pháp tuyến của mp( P) là: n→ = [u→;AB→] = (-4; 14; 8)= -2( 2; -7; -4)

=> Phương trình mặt phẳng ( P) đi qua A(2; -3; 4) và nhận n→ làm VTPT là:

2( x-2) – 7( y+ 3) – 4( z- 4) =0 hay 2x – 7y - 4z- 9=0

Chọn A.

Dạng 4. Viết phương trình mặt phẳng trung trực của đoạn thẳng

1. Phương pháp giải

+ Phương trình mặt phẳng đi qua điểm M (x_o; y_o; z_o) và có vecto pháp tuyến n→(A:B:C) là:

A(x – x_o) + B( y – y_o) + C(z- z_o ) = 0

+ Cho trước hai điểm A và B. Viết phương trình mặt phẳng trung trực của AB :

• Gọi I là trung điểm của AB. Suy ra tọa độ điểm I ( áp dụng công thức trung điểm của đoạn thẳng).

• Mặt phẳng trung trực của AB đi qua điểm I và nhận AB→ làm vecto pháp tuyến

=> Phương trình mặt phẳng trung trực của AB.

2. Ví dụ minh họa

Ví dụ 1: Cho hai điểm A( 2; 1; 0) và B(-4 ; -3; 2) . Viết phương trình mặt phẳng trung trực của AB?

A. 3x + 2y - z+ 6= 0    B. 6x- 4y + 4z+ 3= 0

C. 3x – 2y – 2z+ 4= 0    D. 6x + 4y + 4z+ 1= 0

Hướng dẫn giải:

+ Gọi (P) là mặt phẳng trung trực của AB.

=> Mặt phẳng ( P) nhận AB→ (- 6; -4; 2) làm vecto pháp tuyến. Chọn n→ ( 3; 2; -1)

+ Gọi I là trung điểm của AB; tọa độ điểm I là:

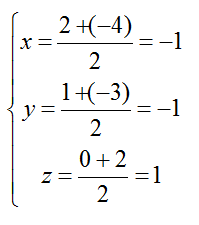
=> I( -1; - 1; 1)

+ Mặt phẳng ( P) qua I (- 1; -1; 1) và vecto pháp tuyến có phương trình là:

3( x+ 1)+ 2( y+ 1) – 1( z – 1) = 0 hay 3x + 2y – z + 6 = 0

Chọn A.

Ví dụ 2: Cho hai điểm A( 0; 2; -3) và B( 4; -4; 1). Gọi M là trung điểm của AB.Viết phương trình mặt phẳng trung trực của OM?

A. 2x + y +z+ 3= 0    B. 2x + y - z+ 3= 0

C. 2x – y – z - 3 = 0    D. 2x – y + z+ 1= 0

Hướng dẫn giải:

+ Do M là trung điểm của AB nên tọa độ của M là:

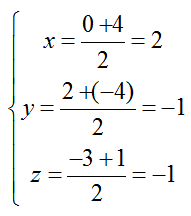
=> M( 2; -1; -1)

+ Gọi (P) là mặt phẳng trung trực của OM.

=> Mặt phẳng ( P) nhận OM→(2;-1;-1) làm vecto pháp tuyến

+ Gọi I là trung điểm của OM; tọa độ điểm I là:

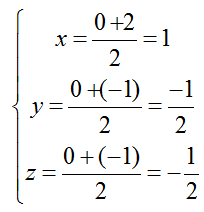
+ Mặt phẳng ( P) qua I và vecto pháp tuyến OM→(2;-1;-1) có phương trình là:

2.(x-1) - 1.(y+1/2) - 1.(z+1/2) = 0 hay 2x – y – z – 3= 0

Chọn C.

Ví dụ 3: Trong mặt phẳng tọa độ Oxyz; cho hai điểm A và B. Gọi I là trung điểm của AB. Viết phương trình mặt phẳng trung trực của AB biết tọa độ điểm A( 1; 2; 0) và I( -2; 1; 1)

A. x + y- z+ 1= 0    B. 3x+ y- z+ 6= 0

C. 3x- y+ z- 1= 0    D. Tất cả sai

Hướng dẫn giải:

+ Gọi (P) là mặt phẳng trung trực của AB .

=> Mặt phẳng ( P) đi qua I và vuông góc AI

=> Mặt phẳng ( P) đi qua I ( -2; 1; 1) và nhận vecto IA→ ( 3; 1; -1) làm vecto pháp tuyến

Phương trình mặt phẳng (P):

3( x+ 2) + 1( y-1) – 1(z- 1) = 0 hay 3x+ y – z+ 6= 0

Chọn B.

Dạng 5. Phương trình mặt phẳng theo đoạn chắn

1. Phương pháp giải

+ Phương trình mặt phẳng (P) đi qua ba điểm A(a; 0; 0) ; B( 0; b; 0) , C(0;0; c) với abc ≠ 0 có phương trình: x/a + y/b + z/c = 1

+ Phương trình mặt phẳng có dạng: x/a + y/b + z/c = 1 cắt ba trục Ox; Oy;Oz lần lượt tại các điểm A(a; 0; 0); B(0; b; 0) và C( 0; 0; c) .

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): 2x - y+ 2z - 4= 0. Viết phương trình mặt phẳng (P) theo đoạn chắn?

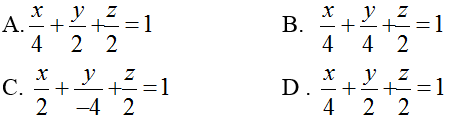
Hướng dẫn giải:

Mặt phẳng ( P) cắt các trục tọa độ Ox; Oy; Oz lần lượt tại A( 2; 0; 0); B( 0; -4; 0) và C(0; 0; 2)

=> Phương trình mặt phẳng ( P) theo đoạn chắn là: x/2 + y/-4 + z/2 = 1

Chọn C.

Ví dụ 2: Trong không gian với hệ toạ độ Oxyz, gọi (P) là mặt phẳng qua G(1; -2; -1) và cắt các trục Ox; Oy; Oz lần lượt tại các điểm A; B; C (khác gốc O) sao cho G là trọng tâm của tam giác ABC. Khi đó mặt phẳng (P) có phương trình:

A. 2x - y+ 2z + 3 = 0    B. 2x – y - 2z – 6 =0

C. 2x + y - 2z + 9 = 0    D. 2x+ y + 3z - 9 =0

Hướng dẫn giải:

Gọi tọa độ ba điểm A( a; 0; 0); B(0; b; 0) và C(0; 0; c) với , khi đó mặt phẳng (P) phương trình có dạng:

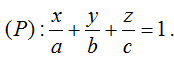
Mà điểm G( 1; 2; 3) là trọng tâm tam giác ABC nên

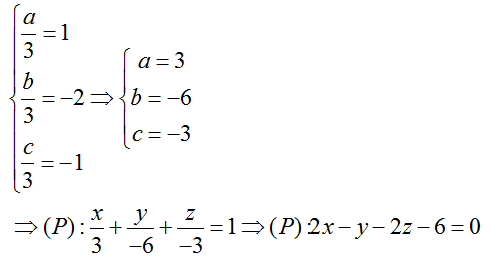
Chọn B.

Ví dụ 3: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P) đi qua điểm H(2; 1;1) và cắt các trục Ox, Oy, Oz lần lượt tại A; B; C (khác gốc toạ độ O) sao cho H là trực tâm tam giác ABC. Mặt phẳng (P) có phương trình là:

A. 2x+ y + z - 6= 0    B. 2x + y + z+ 6 = 0

C. 2x – y + z +6 = 0    D. 2x+ y - z + 6 = 0

Hướng dẫn giải:

Gọi tọa độ ba điểm A(a; 0; 0); B(0; b; 0) và C(0; 0; c) với , khi đó mặt phẳng ( P) phương trình có dạng:

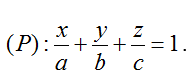
Ta có: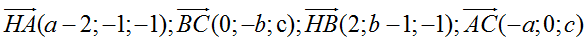

Điểm H(2; 1; 1) là trực tâm tam giác ABC nên

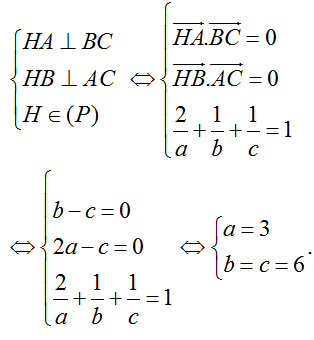
Thay a; b; c vào (1), ta được: (P): x/3 + y/6 + z/6 = 1

hay (P): 2x+ y + z - 6 = 0

Chọn A.

Ví dụ 4: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P) đi qua điểm M(1; 1; 1) và cắt chiều dương các trục Ox, Oy, Oz lần lượt tại A; B; C (khác gốc toạ độ O) sao cho tứ diện OABC có thể tích nhỏ nhất. Mặt phẳng (P) có phương trình là:

A. x – y - z- 3 = 0    B. x+ y+ z+ 3= 0

C. x+ y+ z - 3 = 0    D. x+ y – z+ 3 = 0

Hướng dẫn giải:

Gọi tọa độ ba điểm A(a; 0; 0); B(0; b; 0) và C( 0; 0; c) với a; b;c > 0 . Khi đó phương trình mặt phẳng (P) có dạng:

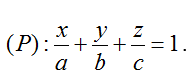
Điểm M(1;1;1) thuộc (P) nên ta có: 1/a + 1/b + 1/c = 1.

Thể tích khối tứ diện OABC: V_O.ABC = 1/6.OA.OB.OC = 1/6 a.b.c

Áp dụng bất đẳng thức Côsi cho ba số dương 1/a; 1/b; 1/c :

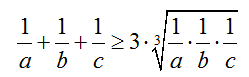
Do 1/a + 1/b + 1/c = 1 nên suy ra abc ≥ 27 => 1/6 ≥ abc ≥ 9/2 .

=> V_OABC đạt giá trị nhỏ nhất bằng 9/2 khi 1/a = 1/b = 1/c = 1/3

⇔ a = b = c = 3

(P): x/3 + y/3 + z/3 = 1 ⇔ x + y + z - 3 = 0

Chọn C

Dạng 6. Viết phương trình mặt phẳng (α) đi qua điểm M và vuông góc với đường thẳng d.

1. Phương pháp giải

+ Đường thẳng d: 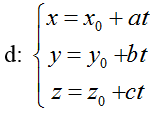nhận vecto u^→(a; b; c) làm vecto chỉ phương.

Đường thẳng : 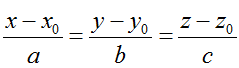nhận vecto u^→(a; b; c) làm vecto chỉ phương.

+ Để viết phương trình mặt phẳng (α) đi qua M và vuông góc với đường thẳng d ta làm như sau:

Tìm vecto chỉ phương của d là u_d→

Vì d ⊥ (α) nên (α) có vecto pháp tuyến là n_α→= u_d→

Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 vecto pháp tuyến n_α→

2. Ví dụ minh họa

Ví dụ 1: Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm O và vuông góc với đường thẳng d:

A. 2x – z = 0    B. –y+ 2z= 0     C. x- y+ 2z= 0     D. x + z = 0

Hướng dẫn giải:

+Đường thẳng d có vecto chỉ phương u_d→(2;0;-1)

+Mặt phẳng (P) vuông góc với đường thẳng (d) nên (P) có một vecto pháp tuyến là:

n_P→ ^→= u_d→(2; 0; -1)

+ Khi đó phương trình mặt phẳng (P) đi qua O và có vecto pháp tuyến n_P→ là:

2(x – 0) + 0 (y -0) – 1. (z – 0) = 0 hay 2x – z = 0

Chọn A.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, cho ba điểm A (-2; 3; -3), B(2; 1; -1) và C(0; 2; 0). Viết phương trình mặt phẳng qua A và vuông góc với đường thẳng BC.

A. 2x+ y – z - 3= 0     B. x+ 2y - 2z + 2 = 0

C. -2x + y + z - 4 = 0    D. x + y + z + 2 = 0

Hướng dẫn giải:

Đường thẳng BC có vecto chỉ phương u→ = BC→ = (-2; 1;1).

Do mặt phẳng (P) vuông góc với đường thẳng BC nên mặt phẳng (P) có vecto pháp tuyến là n→ = BC→ = (-2; 1; 1)

Phương trình mặt phẳng cần tìm là:

-2( x+ 2) + 1. ( y – 3) + 1( z+ 3) = 0 hay -2 x + y+ z – 4= 0

Chọn C.

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz; cho hai điểm A (1; 2; 3) và B( 3; 0; -1). Gọi I là trung điểm của AB. Viết phương trình mặt phẳng ( P) đi qua I và vuông góc với đường thẳng (d): ?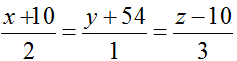

A. 5x+ 27 y - 5z + 12 = 0    B. 2x+ y+ 3z + 8 = 0

C. 2x+ y+ 3z - 8=0    D. 5x+ 27y – 5 z – 7= 0

Hướng dẫn giải:

+ I là trung điểm của AB nên tọa độ điểm I là:

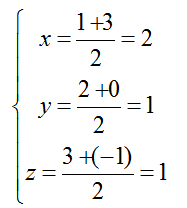
=> I (2; 1; 1)

+ Đường thẳng d có vecto chỉ phương là: u→ (2; 1; 3)

+ Do mặt phẳng ( P ) vuông góc với đường thẳng (d) nên mp (P) có VTPT là n→(2;1;3)

=> Phương trình mặt phẳng ( P) : 2( x-2) + 1( y- 1) + 3( z - 1) =0

Hay 2x+ y+ 3z – 8 = 0

Chọn C.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho tam giác ABC với A (1;0; -1); B(2; 1; -1) Và C( 3; 2; -1). Gọi G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng ( P) đi qua G và vuông góc với đường thẳng (d) : ?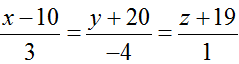

A. 2x - 3y+ z- 10= 0    B. 3x- 4y+ z - 1= 0

C. 3x+ 4y - z + 3= 0    D. 4x- 3y+ 2z - 10= 0

Hướng dẫn giải:

+ Do G là trọng tâm của tam giác ABC nên tọa độ điểm G là:

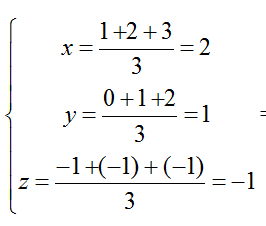
=> G( 2; 1; -1)

+ Đường thẳng d có vecto chỉ phương là: u→(3;-4;1)

.

+ Do mặt phẳng ( P ) vuông góc với đường thẳng (d) nên mp (P) có vecto pháp tuyến là : n→(3;-4;1)

=> Phương trình mặt phẳng ( P): 3( x- 2) – 4( y - 1) + 1( z + 1) = 0

Hay 3x – 4y + z- 1= 0

Chọn B.

Dạng 7: Viết phương trình mặt phẳng (α ) chứa đường thẳng và vuông góc với mặt phẳng (β) .

1. Phương pháp giải

• Tìm vecto pháp tuyến của (β) là n_β→

• Tìm vecto chỉ phương của Δ là u_Δ→

• Vecto pháp tuyến của mặt phẳng α là n_α→

• Lấy một điểm M trên Δ

• Áp dụng cách viết phương trình mặt phẳng đi qua một điểm và có VTPT n_α^→

2. Ví dụ minh họa

Ví dụ 1: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa đường thẳng 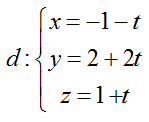và vuông góc với mặt phẳng (Q): x+ 2y - z+ 10 = 0

A. x+ z = 0    B. x+ y +1= 0    C. y - z + 1= 0     D. x – y + 2z= 0

Hướng dẫn giải:

Đường thẳng d đi qua điểm A ( -1; 2; 1) và có vecto chỉ phương u→ (-1;2;1)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→ = (1;2;-1)

Mặt phẳng (P) chứa đường thẳng d và vuông góc với (Q) nên (P) có một vecto pháp tuyến là

n→ =[u→ ,n_Q→ ]= ( - 4; 0; -4) = - 4(1; 0; 1)

Phương trình mặt phẳng (P) đi qua A( -1; 2; 1) và có VTPT n'→ (1; 0; 1) là:

1( x + 1) + 0( y - 2) + 1( z - 1) = 0 hay x+ z = 0

Chọn A.

Ví dụ 2: Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) chứa đường thẳng 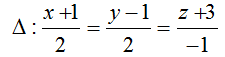và vuông góc với mặt phẳng α : 2x – y + 3z – 98= 0 có phương trình là

A. 2x+ 3y+ 8z- 10= 0    B. 5x+ 8y – 6z- 1= 0

C. 5x+ 8y+ 3z- 1= 0    D.5x - 8y- 6z – 5 = 0

Hướng dẫn giải:

+ Đường thẳng ∆ có vecto chỉ phương là u_∆→ (2;2; -1) và đi qua điểm A( -1; 1; -3).

+ Mặt phẳng (α) có vecto pháp tuyến là: n_α→ ( 2; -1; 3)

+ Mặt phẳng (P) chứa đường thẳng ∆ và vuông góc với mặt phẳng (α) nên (P) có một vecto pháp tuyến là n^→=[u_∆^→ ,n_α^→ ] = (5; -8; -6) và đi qua A(0; -1; 2)

Phương trình mặt phẳng (P) cần tìm là:

5( x+ 1) – 8( y - 1) – 6( z + 3) = 0 hay 5x - 8y - 6z - 5 = 0

Chọn D.

Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(3; 1; 1), B( 2; -1; 2) và mặt phẳng : 2x – y + 2z + 50= 0. Mặt phẳng (P) đi qua hai điểm A; B và vuông góc với mặt phẳng α có phương trình là

A. x – 3y – 5z + 5 = 0    B. 3x - 4y – 5z = 0.

C. 3x - 4y – 5z – 2= 0    D. 3x+ 4y – 5z = 0

Hướng dẫn giải:

Ta có đường thẳng AB nhận AB→ (-1 ; -2 ; 1) làm vecto chỉ phương

Mặt phẳng (α) có vecto pháp tuyến n_α→ (2 ; -1 ; 2)

+ Mặt phẳng (P) đi qua hai điểm AB nên chứa đường thẳng AB và vuông góc với mặt phẳng (α) nên (P) có một VTPT là n^→ = [AB^→ , n_α^→ ] = (-3; 4; 5) và đi qua A(3; 1; 1)

+ Phương trình mặt phẳng (P) cần tìm là:

-3( x- 3) + 4( y-1) + 5( z- 1) = 0 hay -3x + 4y + 5z= 0

Vậy phương trình mp (P): - 3x + 4y+ 5z = 0 ⇔ 3x- 4y- 5z= 0

Chọn B.

Dạng 8: Viết phương trình mặt phẳng (α) chứa đường thẳng Δ và song song với Δ'; (Δ; Δ' chéo nhau).

1. Phương pháp giải

Tìm vecto chỉ phương của ∆; ∆’ là u₁→ ; u₂→

Vecto pháp tuyến của mặt phẳng (α) là n_α→ = [u₁→, u₂→]

Lấy 1 điểm M trên đường thẳng ∆

Áp dụng cách viết phương trình mặt phẳng đi qua một điểm và có 1 vecto pháp tuyến.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa đường thẳng

A.– 6x+ y+ 2z- 3= 0    B. -6x+ y+ 2z+ 3= 0

C. 6x+ y- 2z+ 1= 0    D. 6x- y- 2z+ 4= 0

Hướng dẫn giải:

Đường thẳng d1 đi qua điểm M (1; 1; 1) và có vecto chỉ phương u₁^→(0;-2;1)

Đường thẳng d2 đi qua điểm N (1; 0;1) có vecto chỉ phương u₂^→(1;2;2)

Ta có: [u₁^→,u₂^→] = ( - 6; 1; 2)

Gọi n^→ là một vecto pháp tuyến của mặt phẳng (P) ta có: 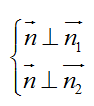nên ^→ cùng phương với [u₁^→,u₂^→] . Chọn n^→ ( -6; 1; 2)

Mặt phẳng (P) đi qua điểm M (1; 1; 1) và nhận VTPT n^→ (-6; 1; 2) có phương trình là:

- 6(x -1) + 1( y- 1) + 2( z - 1)= 0 hay – 6x + y + 2z + 3= 0

Thay tọa độ điểm N vào phương trình mặt phẳng (P) thấy không thỏa mãn.

Vậy phương trình mặt phẳng (P) là – 6x + y + 2z + 3= 0

Chọn B.

Ví dụ 2: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng 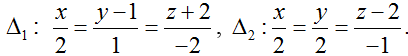Mặt phẳng α chứa ∆₁ và song song với đường thẳng ∆₂ có phương trình là

A. x+ 4y + 2z + 2 = 0    B. 3x – 2y + 2z – 6 = 0

C. 3x – 2y + 2z + 6 = 0    D. x+ 4y+ 2z - 2 = 0

Hướng dẫn giải:

Đường thẳng ∆_1 đi qua điểm M (0; 1; -2) và có vecto chỉ phương u₁^→ (2; 1; -2)

Đường thẳng d_2 đi qua điểm N (0; 0; 2) có vecto chỉ phương u₂^→ (2; 2; -1)

Ta có: [u₁^→, u₂^→] = (3; -2; 2)

Gọi n ^→ là một vecto pháp tuyến của mặt phẳng (P) ta có 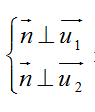nên n^→ cùng phương với [u₁^→, u₂^→] .Chọn n^→ ( 3; -2; 2)

Mặt phẳng (α) đi qua điểm M (0; 1; -2) và nhận VTPT n^→ ( 3; -2; 2) có phương trình là:

3( x- 0) – 2( y – 1) + 2( z+ 2) = 0 hay 3x – 2y + 2z + 6 = 0

Thay tọa độ điểm N vào phương trình mặt phẳng ( thấy không thỏa mãn.

Vậy phương trình mặt phẳng (P) là 3x - 2y + 2z + 6 = 0

Chọn C.

Ví dụ 3: Trong không gian hệ tọa độ Oxyz, cho đường thẳng 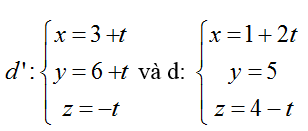.Viết phương trình mặt phẳng (P) chứa d và song song với d’

A. x+ 3y - 2z - 24= 0    B. x+ 3y+ 2z - 24=0

C. x - 3y+ 2z + 12= 0    D. x - 3y - 2z - 1= 0

Hướng dẫn giải:

Đường thẳng d đi qua điểm M (1; 5; 4) và có vecto chỉ phương u₁^→ (2; 0; -1)

Đường thẳng d’ đi qua điểm N (3; 6;0) có vecto chỉ phương u₂^→ (1; 1; -1)

Ta có: [u₁^→, u₂^→] = (1; 3; 2)

Gọi n^→ là một vecto pháp tuyến của mặt phẳng (P) ta có 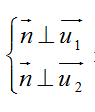nên n^→ cùng phương với [u₁^→, u₂^→]. Chọn n^→(1;3;2) .

Mặt phẳng (P) đi qua điểm M (1; 5; 4) và nhận vecto pháp tuyến n^→(1;3;2) có phương trình là:

1( x -1) + 3( y -5) + 2( z- 4) = 0 hay x+ 3y + 2z – 24= 0

Thay tọa độ điểm N vào phương trình mặt phẳng (P) thấy không thỏa mãn.

Vậy phương trình mặt phẳng (P) là x+ 3y + 2z – 24= 0.

Chọn B.

Ví dụ 4: Trong không gian hệ tọa độ Oxyz, cho bốn điểm A(5; 1; 3), B(1; 6;2), C(5; 0; 4), D(4; 0; 6). Mặt phẳng (P) đi qua hai điểm A, B và song song với đường thẳng CD có phương trình là:

A. 10x+ 9y + 5z - 74= 0    B. 10x – 9y – 5z+ 2= 0

C. 10x - 9y + 5z + 56= 0    D. Đáp án khác

Hướng dẫn giải:

Ta có: AB^→ (- 4; 5; -1); CD^→( -1; 0; 2) =>[AB^→, CD^→] = ( 10; 9; 5)

Gọi n^→ là một vecto pháp tuyến của mặt phẳng (P)

Do A, B thuộc mặt phẳng (P), mặt phẳng (P) song song với đường thẳng CD nên ta có 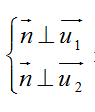nên n^→ cùng phương với [AB^→, CD^→] . Chọn n^→ (10; 9; 5)

Vậy phương trình mặt phẳng (P) có VTPT n^→ (10; 9; 5) và đi qua điểm A(5; 1; 3) là:

10. (x – 5) + 9( y- 1)+ 5( z- 3) =0 hay 10x + 9y + 5z – 74 =0

Thay tọa độ C, D vào phương trình thấy không thỏa mãn.

Vậy phương trình mặt phẳng cần tìm là 10x +9y + 5z – 74= 0

Chọn A.

Dạng 9. Viết phương trình mặt phẳng chứa đường thẳng d và đi qua điểm M không thuộc d

1. Phương pháp giải

• Tìm vecto chỉ phương của đường thẳng d là u^→ . Lấy 1 điểm N trên d, tính tọa độ vecto MN^→

• Vecto pháp tuyến của mặt phẳng (P) là n^→ = [u^→, MN^→]

• Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có vecto pháp tuyến.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian hệ tọa độ Oxyz, cho điểm A (4; -3; 1) và đường thẳng d: 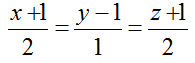. Viết phương trình mặt phẳng (P) chứa điểm A và đường thẳng d.

A. 10x+ 6y – 13z + 1= 0    B. 10 x – 6y- 13z + 12 = 0

C. 10x + 6y – 13z – 9 = 0    D. 10x – 6y – 13z+ 19 = 0

Hướng dẫn giải:

Đường thẳng d đi qua điểm N(-1; 1; -1) và có vecto chỉ phương u^→(2;1; 2); AN^→( - 5; 4; -2)

Mặt phẳng (P) chứa đường thẳng d và đi qua điểm A nên (P) có một vecto pháp tuyến là

n^→ = [u^→; AN^→] = ( - 10; -6; 13) = - (10; 6; -13)

Phương trình mặt phẳng (P) là:

10(x – 4) + 6 ( y+ 3) – 13( z- 1) = 0 hay 10x + 6y – 13z – 9 = 0

Chọn C.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, mặt phẳng (P) qua điểm A(0; 0; 2) và chứa trục hoành có phương trình là:

A. y= 0    B. y= 2    C. z= 2    D. x= 0

Hướng dẫn giải:

Trục hoành đi qua gốc tọa độ O(0; 0; 0) và có vecto chỉ phương u^→(1; 0; 0) ; OA^→(0; 0; 2)

Mặt phẳng (P) chứa đường thẳng d và đi qua điểm A nên (P) có một vecto pháp tuyến là

n^→ = [u^→; OA^→] = (0; -2; 0) = -2 (0; 1;0)

Phương trình mặt phẳng (P) là: 0( x- 0) + 1( y-0) + 0(z - 2) = 0 hay y = 0

Chọn A.

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz; mặt phẳng (P) đi qua A( 1; 2; 3) và chứa đường thẳng d: 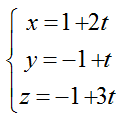Phương trình mặt phẳng (P) có dạng 5x+ ay+ bz+ c= 0. Tính a+ b+ c?

A. - 1     B. 3     C. 2     D. 5

Hướng dẫn giải:

+ Đường thẳng d đi qua điểm N(1; -1; -1) và có vecto chỉ phương u^→(2; 1; 3); AN^→(0; -3; -4)

Mặt phẳng (P) chứa đường thẳng d và đi qua điểm A nên (P) có một vecto pháp tuyến là

n^→ = [u^→;AN^→] = ( 5; 8; -6)

Phương trình mặt phẳng (P) là: 5( x- 1)+ 8( y-2) – 6( z- 3) = 0 hay 5x+ 8y- 6z – 3= 0

=> a+ b+ c = 8+ (-6) + (-3) = - 1

Chọn A.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P) đi qua điểm A(1; 2; 1); B( 1; -2; 0) và C(2; 1; 2). Phương trình mặt phẳng ( P) có dạng : 5x+ ay+ bz+ c= 0. Tính a.b.c?

A. 10     B. – 8     C. 6     D.12

Hướng dẫn giải:

+ Ta có: AB^→ (0; -4; -1); BC^→ ( 1; 3; 2)

+ Mặt phẳng (P) đi qua ba điểm A; B và C nên (P) có một vecto pháp tuyến là

n^→ = [AB^→, BC^→] = (- 5; -1; 4) = - ( 5; 1; -4)

=> Phương trình mặt phẳng (P) là:

5(x- 1) +1( y- 2) – 4( z- 1) = 0 hay 5x+ y – 4z -3= 0

=> a= 1; b= -4 và c= -3 nên a.b.c= 1.(-4).(-3) = 12

Chọn D.

Dạng 10: Viết phương trình mặt phẳng (P) chứa 2 đường thẳng cắt nhau d và d’

1. Phương pháp giải

• Tìm vecto chỉ phương của d và d’ là u₁^→; u₂^→

• Vecto pháp tuyến của mặt phẳng (P) là n^→ = [u₁^→; u₂^→]

• Lấy 1 điểm M trên d

• Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có vecto pháp tuyến.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) chứa hai đường thẳng

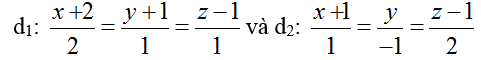có phương trình là

A. (P): x+ y- z+ 2= 0    B. (P) : x- y- z+ 2= 0

C. (P) : x- z+ 2= 0    D. Không tồn tại.

Hướng dẫn giải:

Đường thẳng d1 đi qua điểm M(-2; -1; 1) và có vecto chỉ phương u₁→ (2; 1; 1)

Đường thẳng d2 đi qua điểm N(-1; 0; 1) và có vecto chỉ phương u₂→ (1; -1; 2)

Ta có: [u₁→,u₂→] = ( 3; -3; -3); MN₁→ (1; 1;0)

Do MN→ . [u₁→,u₂→] = 3. 1+ (- 3).1+ (- 3). 0 = 0 nên đường thẳng d1 và d2 cắt nhau.

Mặt phẳng (P) chứa đường thẳng d1 và d2 cắt nhau nên (P) có một vecto pháp tuyến là

n→ = [u₁→,u₂→] = (3; -3; -3) = 3( 1; -1; -1)

Phương trình mặt phẳng (P) là:

1( x+ 2) – 1( y+ 1) - 1( z- 1) = 0 hay x- y - z + 2= 0

Chọn B.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, phương trình mặt phẳng (P) chứa hai đường thẳng 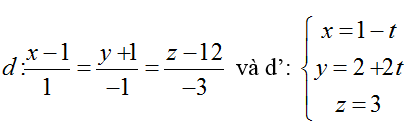có dạng 6x+ ay+ bz+c= 0. Tính a+ b+ c?

A. 10     B. -11     C. 11    D. 8

Hướng dẫn giải:

Đường thẳng d đi qua điểm M(1; -1; 12) và có vecto chỉ phương u₁→ (1; -1; -3)

Đường thẳng d’ đi qua điểm N(1; 2; 3) và có vecto chỉ phương u₂→ (-1; 2; 0)

Ta có: [u₁→, u₁→]= ( 6; 3; 1); MN→ ( 0; 3; -9)

Do MN→. [u₁→, u₁→] = 0 nên đường thẳng d và d’ cắt nhau.

Mặt phẳng (P) chứa đường thẳng d và d’ cắt nhau nên (P) có một vecto pháp tuyến là

n→ = [u₁→, u₂→] = (6; 3; 1)

Phương trình mặt phẳng (P) là:

6( x- 1)+ 3( y – 2) + 1( z- 3) =0 hay 6x + 3y + z – 15= 0

=> a= 3; b= 1; c= -15 nên a+ b+ c= 3+ 1+ (-15) = -11.

Chọn B

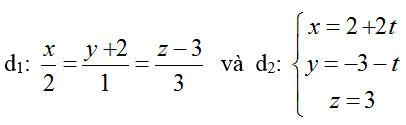
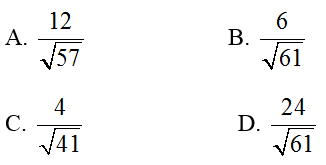Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng có dạng 6x+ ay+ bz+c= 0. Tính a+ b+ c?. Gọi mặt phẳng (P) chứa d₁ và d₂. Tính khoảng cách từ điểm I( 2; 1; 3) đến mặt phẳng (P)?

có dạng 6x+ ay+ bz+c= 0. Tính a+ b+ c?

Hướng dẫn giải:

Đường thẳng d₁ đi qua điểm M(0; -2; 3) và có vecto chỉ phương u₁→ (2; 1; 3)

Đường thẳng d₂ đi qua điểm N(2; -3; 3) và có vecto chỉ phương u₂→ (2; -1; 0)

Ta có: [u₁→, u₂→] =( 3; 6; -4); MN^→ ( 2; -1; 0)

Do MN→.[u₁→, u₂→] = 3.2+ 6.(-1) + (-4). 0 = 0 nên đường thẳng d₁ và d₂ cắt nhau.

Mặt phẳng (P) chứa đường thẳng d1 và d2 cắt nhau nên (P) có một vecto pháp tuyến là

n→ = [u₁→, u₁→] = ( 3; 6; -4)

Phương trình mặt phẳng (P) là:

3( x-0) + 6( y+2) – 4( z-3) = 0 hay 3x+ 6y – 4z+ 24= 0

Khoảng cách từ điểm I( 2; 1; 3) đến mặt phẳng (P) là:

Chọn D.

Dạng 11: Viết phương trình mặt phẳng chứa 2 đường thẳng song song d và d’

1. Phương pháp giải

• Tìm vecto chỉ phương của d và d’ là u₁^→;u₂^→ lấy M thuộc d; N thuộc d’

• Vecto pháp tuyến của mặt phẳng (P) là n^→ = [u₁^→; MN^→]

• Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 vecto pháp tuyến.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa hai đường thẳng

A. 6x+ 3y+ z-10= 0    B. 6x+ 3y+ z- 15 = 0

C. 6x- 3y+ z- 14= 0    D . Đáp án khác

Hướng dẫn giải:

Đường thẳng d đi qua điểm M (1; -1;12) và có vecto chỉ phương u₁→(1; -1; -3)

Đường thẳng d’ đi qua điểm N (1; 2;3) và có vecto chỉ phương u₂→(1; -1; -3)

Ta có: [u₁→,u₂→] = (0; 0; 0); MN^→(0;3; -9)

Do [u₁→,u₁→] = (0; 0; 0) nên đường thẳng d và d’ song song với nhau.

Mặt phẳng (P) chứa đường thẳng d và d’ song song nên (P) có một vecto pháp tuyến là

n→ = [u₁→,MN→] = (18, 9, 3) = 3( 6; 3; 1)

Phương trình mặt phẳng (P) có vecto pháp tuyến (6; 3; 1) và đi qua điểm N (1; 2; 3) là:

6( x – 1)+ 3(y -2) +1(z – 3) = 0 hay 6x + 3y + z - 15 = 0

Chọn B.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa trục Oz và đường thẳng

A. x+ 3x= 0     B. y+ 3z= 0     C. x+ 3y= 0     D. z= 0

Hướng dẫn giải:

Trục Oz đi qua điểm O (0; 0; 0) và có vecto chỉ phương u₁→(0; 0; 1).

Đường thẳng d đi qua điểm N (3; -1;5) và có vecto chỉ phương u₂→( 0; 0; 2)

Ta có: [u₁→, u₁→] = (0; 0; 0); ON^→ = (3; -1; 5)

Do [u₁→, u₂→] = (0; 0; 0) nên đường thẳng Oz và d song song.

Mặt phẳng (P) chứa đường thẳng Oz và d song song nên (P) có một vecto pháp tuyến là

n→ = [u₁→, ON→] = (1; 3; 0)

Phương trình mặt phẳng (P) có VTPT n→ (1; 3; 0) và đi qua điểm O (0; 0; 0) là: x+ 3y = 0

Chọn C.

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz; viết phương trình mặt phẳng (P) đi qua A( -1; 2; 1); B( 0; 4; - 2) và chứa đường thẳng d:

A. 7x + y + 3z+ 2= 0    B. 7x - 6y+ z- 10= 0

C. 7x - y + 3z- 16= 0    D. 7x - y + z + 10= 0

Hướng dẫn giải:

+ Đường thẳng d đi qua điểm M( 0; 1; -1) và có vecto chỉ phương u→( 1; 2; -3).

Vecto AB→ (1; 2; -3); AM→(1; -1; -2)

+ Ta có: [AB→; u→] = (0; 0; 0)

Suy ra: đường thẳng d và AB song song với nhau.

Mặt phẳng (P) chứa A(-1; 2; 1), nhận vecto n→ = [AM→; u→] = ( - 7; -1; -3) = -( 7; 1;3) làm VTPT

=> Phương trình mặt phẳng (P) :

7( x+ 1) + 1( y-2) + 3( z- 1)= 0 hay 7x+ y + 3z + 2= 0

Chọn A.

Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng 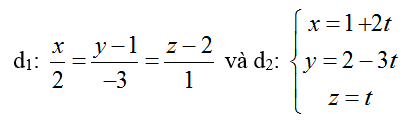. Gọi mặt phẳng (P) chứa d1và d2. Biết mặt phẳng (P) có phương trình dạng: x+ ay+ bz+ c= 0. Tính a.b.c?

A. 8     B. - 5     C. 12     D. -3

Hướng dẫn giải:

Đường thẳng d1 đi qua điểm M( 0;1;2) và có vecto chỉ phương u₁→(2; -3; 1)

Đường thẳng d2 đi qua điểm N( 1;2; 0) và có vecto chỉ phương u₂→(2; -3; 1)

Ta có: [u₁→; u₂→] =(0; 0; 0); MN^→ (1; 1; -2)

Do [u₁→; u₂→] = (0; 0; 0) nên đường thẳng d1 và d2 song song với nhau.

Mặt phẳng (P) chứa đường thẳng d1 và d2 song song với nhau nên (P) có VTPT là

n→ = [u₁→; u₂→] = (5; 5;5) chọn ( 1; 1; 1)

Phương trình mặt phẳng (P) là:

1( x- 0) + 1( y- 1) + 1( z-2) = 0 hay x + y + z - 3= 0

=> a= 1; b= 1 và c= - 3 nên a.b.c= -3

Chọn D.

Dạng 12. Viết phương trình mặt phẳng (P) đi qua một điểm M và song song với hai đường thẳng chéo nhau d và d’ cho trước

1. Phương pháp giải

• Tìm vecto chỉ phương của d và d’ là u₁→; u₂→

• Vecto pháp tuyến của mặt phẳng (P) là n→ = [u₁→, u₂→]

• Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 vecto pháp tuyến.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng 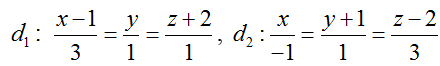Mặt phẳng (α) đi qua A( 2; 1; 2) và đồng thời song song với cả hai đường thẳng d₁; d₂ có phương trình là

A. x+ 5y+ 2z – 10= 0    B. x- 2y+ z – 2= 0

C. x - 5y+ 2z – 1= 0    D. 2x- y + 2z – 7 = 0

Hướng dẫn giải:

Đường thẳng d₁ đi qua M (1; 0; -2) và có vecto chỉ phương u₁→( 3; 1;1)

Đường thẳng d’ đi qua N (0; -1; 2) và có vecto chỉ phương u₂→(-1; 1; 3)

Ta có: [u₁→, u₂→] = (2; -10; 4)

Gọi n→ là VTPT của mặt phẳng (P). Ta có (P) song song với d₁ và d₂ nên 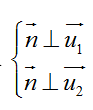nên n^→ cùng phương với [u₁^→, u₂^→]

Chọn n→( 1; -5; 2) ta được phương trình mặt phẳng (P) là:

1.( x – 2) – 5 ( y – 1) + 2(z- 2) =0 hay x- 5y + 2z – 1 = 0

Chọn C.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm B(1; -3; 2) và song song với trục Ox, Oy

A. x= 1     B. y+ 3= 0     C. z- 2= 0     D. 3x+ y= 0

Hướng dẫn giải:

Trục Ox có vecto chỉ phương u₁→(1; 0; 0)

Trục Oy có vecto chỉ phương u₂→(0; 1; 0)

Ta có: [u₁→, u₂→] = (0; 0; 1)

Gọi n→ là VTPT của mặt phẳng (P). Ta có (P) song song với Ox và Oy nên 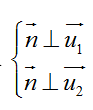nên n^→ cùng phương với [u₁^→, u₂^→]

Chọn n→(0; 0; 1) ta được phương trình mặt phẳng (P) là:

0(x- 1) + 0( y+ 3) + 1( z- 2) = 0 hay z - 2 = 0

Chọn C.

Ví dụ 3: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M (0; -3; 4) và song song với đường thẳng d: 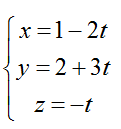và trục Oz

A. 2x+ 3y- z+ 13= 0    B. 3x+ 2y+ 6= 0

C. 3y+2z + 1= 0    D. 4x- 3y – z- 5= 0

Hướng dẫn giải:

Đường thẳng d có vecto chỉ phương u₁→(- 2 ;3; -1)

Trục Oz có vecto chỉ phương u₂→(0; 0;1)

Ta có: [u₁→, u₂→] = ( 3; 2; 0)

Gọi n→ là VTPT của mặt phẳng (P). Ta có (P) song song với Oz và d nên 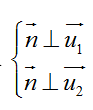nên n^→ cùng phương với [u₁^→, u₂^→]

Chọn n→(3; 2; 0) ta được phương trình mặt phẳng (P) là:

3( x- 0) + 2( y +3) + 0( z - 4) = 0 hay 3x + 2y+ 6 = 0

Chọn B.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; viết phương trình mặt phẳng (P) đi qua A( -1; 2; 1) và song song với đường thẳng BC và đường thẳng d: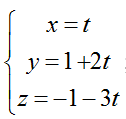; biết điểm B( 0; 1; -3) và C( -2; 1; 0)?

A. 2x + y + 3z- 3= 0    B. 6x + 3y+ 4z - 4= 0

C. 2x - y + z + 3= 0    D. 6x - 3y + 4z + 8= 0

Hướng dẫn giải:

+ Đường thẳng d có vecto chỉ phương u→(1; 2; -3).

Đường thẳng BC có vecto chỉ phương BC→( -2; 0; 3)

Ta có: [u→, BC→] = ( 6; 3; 4)

Gọi n→ là VTPT của mặt phẳng (P). Ta có (P) song song với BC và d nên 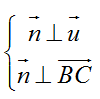nên n^→ cùng phương với [u^→, BC^→]

Chọn n→( 6; 3; 4) ta được phương trình mặt phẳng (P) là:

6 (x+ 1) + 3( y- 2) + 4.(z- 1) = 0 hay 6x +3y + 4z – 4= 0

Chọn B.

Dạng 13. Viết phương trình mặt phẳng (α) đi qua một điểm M và vuông góc với 2 mặt phẳng (P), (Q) cho trước

1. Phương pháp giải

• Tìm vecto pháp tuyến của (P) và (Q) là n₁→ và n₂→

• Vecto pháp tuyến của mặt phẳng (α) là n→ = [n₁→, n₂→]

• Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 vecto pháp tuyến.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x- y + z – 3 = 0 và (Q): 2x – z + 2= 0. Mặt phẳng (α) đi qua O và đồng thời vuông góc với hai mặt phẳng (P), (Q) có phương trình là

A. 2x + 6y + 4z - 1= 0    B. x+ 4y + 3z = 0

C. x- 3y + 2z = 0    D. x + 3y + 2z = 0

Hướng dẫn giải:

Vecto pháp tuyến của mặt phẳng (P) là n₁→(1; -1; 1)

Vecto pháp tuyến của mặt phẳng (Q) là n₂→(2; 0; -1)

Ta có: [n₁→, n₂→] = ( 1; 3; 2) nên mặt phẳng (α) nhận (1; 3; 2) là một vecto pháp tuyến và (P) đi qua điểm O(0; 0; 0) nên mặt phẳng (α) có phương trình:

1. (x – 0) + 3( y – 0) + 2(z – 0) = 0 hay x+ 3y + 2z = 0

Chọn D.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(0; 1; 5), đồng thời vuông góc với cả hai mặt phẳng (Q): 3x – 2y + 2z + 1 = 0 và (R): 5x – 4y + 3z + 10 =0

A. 2x+ y - 2z + 9 = 0    B. x+ 2y- z + 3 = 0

C. 2x- y – 2z + 11 = 0    D. Đáp án khác

Hướng dẫn giải:

Vecto pháp tuyến của mặt phẳng (Q) là n₁→( 3; -2; 2)

Vecto pháp tuyến của mặt phẳng (R) là n₂→( 5; -4; 3)

Ta có: [n₁→, n₂→] = (2; 1; -2) nên mặt phẳng (P) nhận (2; 1; -2) là một vecto pháp tuyến và (P) đi qua điểm M (0; 1; 5) nên mặt phẳng (P) có phương trình:

2.(x – 0) + 1(y - 1) - 2( z - 5) = 0 hay 2x+ y – 2z + 9= 0

Chọn A.

Ví dụ 3: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm A ( 3; 2; -1), đồng thời vuông góc với mặt phẳng Oxy và mặt phẳng (Q): x + 2y – z + 9 = 0.

A. y+ z - 1= 0     B. 2y – z – 5 = 0

C. 2x- y - 4= 0     D. x+ 2y – 7= 0

Hướng dẫn giải:

Mặt phẳng Oxy có vecto pháp tuyến n₁→(0; 0; 1)

Vecto pháp tuyến của mặt phẳng (Q) là n₂→( 1; 2; -1)

Ta có: [n₁→, n₂→] = ( - 2; 1; 0) nên mặt phẳng (P) nhận ( 2; -1; 0) là một VTPT và (P) đi qua điểm A (3; 2; -1) nên mặt phẳng (P) có phương trình:

2( x- 3) - 1( y – 2)+ 0( z+ 1)= 0 hay 2x – y – 4= 0

Chọn C.

Dạng 14: Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q) và cách (Q): Ax+ By + Cz + D = 0 ( hoặc điểm H) một khoảng k cho trước.

1. Phương pháp giải

• Trên mặt phẳng (Q) chọn một điểm M

• Do mặt phẳng (P) song song với mặt phẳng (Q) nên mặt phẳng (P) có dạng: Ax+ By+ Cz + D’= 0

• Sử dụng công thức khoảng cách: d((P); (Q)) = d(M; (Q))= k để tìm D’.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): x + 2y - 2z + 1 = 0 và cách (Q) một khoảng bằng 3.

A. x + 2y - 2z + 4= 0 hoặc x + 2y - 2z – 2= 0

B. x + 2y - 2z+ 3= 0 hoặc x + 2y - 2z – 3= 0

C. x + 2y - 2z – 8= 0 hoặc x + 2y - 2z + 10= 0

D. Tất cả sai

Hướng dẫn giải:

Trên mặt phẳng (Q) chọn điểm M (-1; 0;0)

Do mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng:

x+ 2y – 2z + D = 0

Vì khoảng cách giữa 2 mặt phẳng (P) và (Q) bằng 3 nên ta có:

d(M; (P))= 3

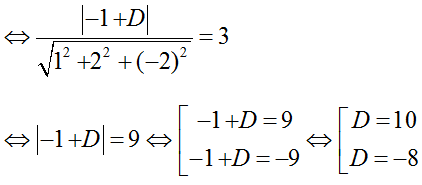
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là

x+ 2y – 2z + 10 = 0 hoặc x+ 2y - 2z – 8= 0

Chọn C.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): 2x+ 3y – z + 3 = 0 và cách (Q) một khoảng bằng √14

A. 2x+ 3y - z + 1= 0 hoặc 2x+ 3y – z – 3= 0

B. 2x+ 3y – z – 11= 0 hoặc 2x + 3y – z + 17= 0

C. 2x+ 3y – z+ 4= 0 hoặc 2x + 3y – z - 6= 0

D. Tất cả sai

Hướng dẫn giải:

Trên mặt phẳng (Q) chọn điểm M (0; -1;0)

Do mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng:

2x + 3y – z + D = 0

Vì khoảng cách giữa 2 mặt phẳng (P) và (Q) bằng √14 nên ta có:

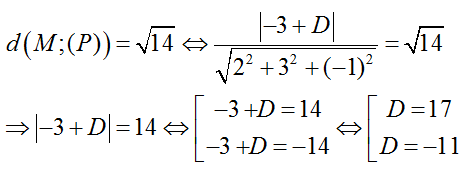
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là :

x+ 2y – 2z + 17 = 0 hoặc x + 2y – 2z – 11= 0

Chọn B.

Ví dụ 3: Trong không gian hệ tọa độ Oxyz, gọi (α) là mặt phẳng song song với mặt phẳng

(β): 2x - 4y + 4z + 3 = 0 và cách điểm A(2; -3; 4) một khoảng bằng 3. Viết phương trình mặt phẳng (α)?

A. 2x- 4y + 4z – 14= 0 hoặc 2x – 4y+ 4z – 50 = 0

B. 2x- 4y+ 4z + 12= 0 hoặc 2x- 4y + 4z – 50 = 0

C. 2x- 4y+ 4z – 14= 0 hoặc 2x- 4y + 4z + 16= 0

D. Đáp án khác

Hướng dẫn giải:

Mặt phẳng (α) song song với mặt phẳng (β) nên phương trình mặt phẳng (α) có dạng:

2x - 4y + 4z + D = 0 (D ≠ 3)

Vì d(A; (P))= 3

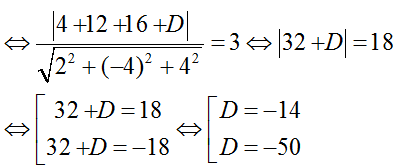
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là

2x - 4y+ 4z – 14= 0 và 2x – 4y + 4z – 50 = 0

Chọn A.

Ví dụ 4: Trong không gian hệ tọa độ Oxyz, cho 3 điểm A(1; 0; 0), B(0; -2; 0); C(0; 0; 4). Viết phương trình mặt phẳng (P) song song với mặt phẳng (ABC) và cách điểm M(2; -1; -1) một khoảng bằng √21

A. 4x- 2y+ z- 20= 0 hoặc 4x- 2y + z + 10= 0

B. 4x+ 2y + z – 17= 0 hoặc 4x+ 2y + z + 10= 0

C. 4x- 2y+ z+ 12= 0 hoặc 4x- 2y + z – 30 = 0

D. 4x+ 2y + z- 10= 0 hoặc 4x + 2y + z+ 8= 0

Hướng dẫn giải:

Phương trình mặt phẳng (ABC) là: x/1 + y/(-2) + z/4 = 1 hay 4x - 2y + z – 4= 0

Mặt phẳng (P) song song với mặt phẳng (ABC) nên phương trình mặt phẳng (P) có dạng:

4x – 2y + z + D = 0 ( D ≠ -4 )

Do khoảng cách từ M đến mặt phẳng (P) bằng √21 nên ta có:

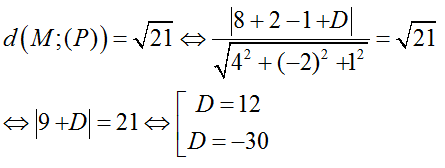
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là

4x – 2y + z – 30 = 0 và 4x – 2y + z + 12= 0

Chọn C.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho ba điểm A(1; 0; 2); B( -1;2; 1) và C( 0; 2; 3). Gọi (P) là mặt phẳng song song với mặt phẳng ( ABC) và cách điểm M( 2; 1;-2) một khoảng là √29. Viết phương trình mặt phẳng ( P) ?

A. 4x+ 3y – 2z+ 1= 0 hoặc 4x + 3y – 2z – 10= 0

B. 4x+ 3y – 2z - 44 = 0 hoặc 4x + 3y – 2z + 14= 0

C. 4x- 3y – 2z + 10= 0 hoặc 4x - 3y – 2z – 16= 0

D. 4x- 3y – 2z + 18= 0 hoặc 4x – 3y – 2z – 24= 0

Hướng dẫn giải:

+ Viết phương trình mặt phẳng (ABC) : AB→(-2; 2; -1); AC→(-1; 2; 1)

=> [AB→, AC→] = ( 4; 3; -2)

Măt phẳng ( ABC) đi qua điểm A(1; 0; 2) và nhận vecto n→( 4; 3; -2) làm VTPT.

Phương trình mặt phẳng ( P):

4( x- 1) + 3( y- 0) -2( z- 2) = 0 hay 4x+ 3y – 2z = 0.

+ Mặt phẳng (P) song song với mặt phẳng (ABC) nên phương trình mặt phẳng (P) có dạng:

4x + 3y – 2z + D = 0 (D ≠ 0)

Do khoảng cách từ M đến mặt phẳng (P) bằng √29 nên ta có:

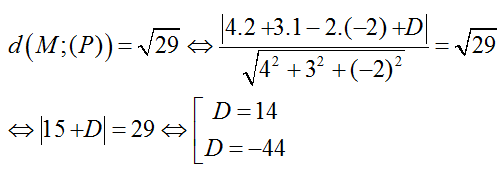
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là

4x + 3y – 2z - 44 = 0 và 4x + 3y – 2z + 14 = 0

Chọn B.

Dạng 15. Viết phương trình mặt phẳng (P) liên quan đến mặt cầu (S).

1. Phương pháp giải

• Tìm tọa độ tâm I và tính bán kính của mặt cầu (S)

• Nếu mặt phẳng (P) tiếp xúc với mặt cầu (S) tại M ∈ (S) thì mặt phẳng (P) đi qua điểm M và có vecto pháp tuyến là MI^→.

• Khi bài toán không cho tiếp điểm thì ta phải sử dụng các dữ kiện của bài toán để tìm VTPT của mặt phẳng và viết phương trình mặt phẳng: Ax+ By+ Cz +D = 0 (D chưa biết)

Sử dụng điều kiện khoảng cách để tìm D

2. Ví dụ minh họa

Ví dụ 1: Trong không gian hệ tọa độ Oxyz, gọi (P) là mặt phẳng song song với mặt phẳng Oxz và cắt mặt cầu (S): (x - 1)² + ( y+ 2)² + z² = 12 theo đường tròn có chu vi lớn nhất. Phương trình của mặt phẳng (P) là:

A. x+ 12= 0    B. y+ z= 0     C. y - 4= 0     D. y+ 2= 0

Hướng dẫn giải:

Mặt cầu (S) có tâm I(1; -2; 0) và bán kính R = 2√3 .

Mặt phẳng Oxz có phương trình y= 0

Mặt phẳng (P) song song với mặt phẳng Oxz nên phương trình mặt phẳng (P) có dạng:

y + D = 0 (D ≠ 0)

Mặt phẳng (P) cắt mặt cầu (S) theo đường tròn có chu vi lớn nhất nên mặt phẳng (P) đi qua tâm I của mặt cầu.

Thay tọa độ tâm I vào phương trình mặt phẳng (P) ta được : - 2+ D = 0 nên D = 2

Phương trình mặt phẳng (P) là: y+ 2= 0

Chọn D.

Ví dụ 2: Trong không gian với hệ trục toạ độ Oxyz,cho mặt cầu (S): (x-1)² +(y- 2)² +(z- 3)² = 9, điểm A( 0; 0; 2) . Mặt phẳng ( P) đi qua A và cắt mặt cầu ( S) theo hình tròn (C) có diện tích nhỏ nhất. Tìm một vecto pháp tuyến của (P) ?

A. n^→(1;2;3).    B. n^→(1;2;1).    C.n^→(1;2;0) .    D. n^→(1;-2;1).

Hướng dẫn giải:

Mặt cầu (S) có tâm I(1; 2; 3) và bán kính R= 3.

Ta có 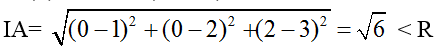nên điểm A nằm trong mặt cầu.

Ta có :

Diện tích hình tròn (C) là: S= 4πr² nên diện tích hình tròn ( C) nhỏ nhất khi và chỉ khi r nhỏ nhất ⇔ d(I,(P)) lớn nhất.

Do d(I,(P)) ≤ IA nên maxd(I; (P)) = IA

Khi đó mặt phẳng (P) đi qua A và nhận IA^→(-1;-2;-1) làm vecto pháp tuyến.

Mà vecto n^→(1; 2; 1) cùng phương với vecto IA^→ nên n^→(1; 2; 1) là vecto pháp tuyến của (P).

Chọn B.

Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) : 2x – 2y – 2z + 18= 0 và mặt cầu (S): x² + y² + z² – 2x + 2y – 4z – 3= 0.Tiếp diện của (S) song song với (P) có phương trình ?

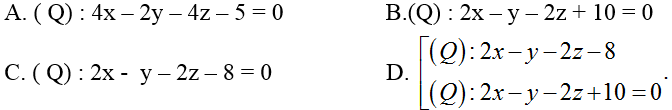
Hướng dẫn giải:

Vì mp (Q) // (P) nên mặt phẳng (Q) có dạng: 2x – y – 2z + m = 0 .

Mặt cầu (S) có tâm I( 1; -1; 2) và bán kính R = 3.

Mà (Q) là tiếp diện của mặt cầu (S) nên d(I; (Q)) = R

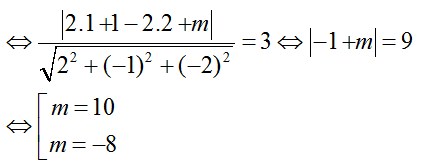
Vậy phương trình mặt phẳng (Q) cần tìm là: 2x- y – 2z – 8= 0 hoặc 2x – y - 2z + 10 = 0

Chọn D.

Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P): 2x + 2y + z - 15 = 0 và mặt cầu (S): x² + y² + z² – 2x – 4y + 4z - 16 = 0. Mặt phẳng (Q) song song với (P) và cắt mặt cầu (S) theo giao tuyến là đường tròn có diện tích 16π. Khi đó (Q) có phương trình là

A.(Q): 2x + 2y + z+ 5 = 0 hoặc 2x+ 2y + z – 13 = 0

B.(Q): 2x + 2y + z -19 = 0 hoặc 2x+ 2y + z+ 1= 0

C.(Q): 2x + 2y + z – 3= 0 hoặc 2x + 2y + z +15 = 0

D.(Q): 2x + 2y + z – 7 = 0 hoặc 2x + 2y + z + 11 = 0

Hướng dẫn giải:

+ Vì mặt phẳng (Q) song song với mặt phẳng (P) nên mặt phẳng (Q) có dạng :

(Q) : 2x+ 2y + z + m = 0 (m ≠ -15)

+ Mặt cầu ( S) có tâm I( 1 ; 2 ; -2) và bán kính R= 5.

Gọi r là bán kính đường tròn giao tuyến, khi đó :

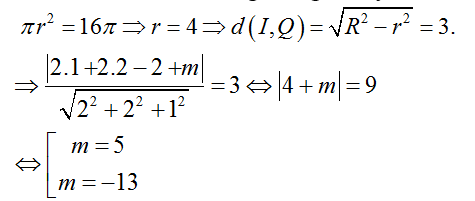
Vậy phương trình mặt phẳng ( Q) : 2x+ 2y + z+ 5= 0 hoặc 2x+ 2y +z – 13= 0

Chọn A

Ví dụ 5: Trong không gian với hệ trục tọa độ Oxyz; cho mặt cầu (S):(x - 2)² + ( y - 1)² + z² = 16. Mặt phẳng (P): 2x+ 2y- z = 0 cắt mặt cầu theo một đường tròn ( C) có bán kính r. Tính r?

A. 2     B. 3     C. 2√3     D. √3

Hướng dẫn giải:

+ Mặt cầu (S) có tâm I( 2; 1; 0) và bán kính R= 4.

+ Khoảng cách từ tâm I đến mặt phẳng (P):

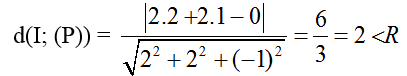
Suy ra, mặt phẳng ( P) cắt mặt cầu (S) theo một đường tròn (C) có bán kính:

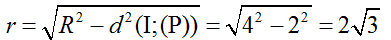
Chọn C.

Dạng 16. Khoảng cách từ một điểm đến mặt phẳng

1. Phương pháp giải

Trong không gian Oxyz, cho điểm A(x_o; y_o;z_o) và mặt phẳng (P): Ax+ By + Cz + D = 0

+ Khi đó, khoảng cách từ điểm A đến mặt phẳng (P) được tính theo công thức:

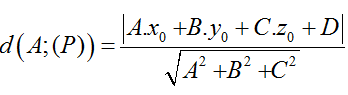
+ Nếu đường thẳng d song song với mặt phẳng (P) thì khoảng cách giữa đường thẳng d và mặt phẳng (P) bằng khoảng cách từ một điểm bất kì của đường thẳng d đến mặt phẳng (P).

+ Nếu hai mặt phẳng (P) và (Q) song song với nhau thì khoảng cách hai mặt phẳng này bằng khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian tọa độ Oxyz, khoảng cách từ điểm A(1; 1;2) đến mặt phẳng : x+ 2y- 2z – 2= 0 bằng:

A. 3    B. 1    C. 13/3    D. 1/3

Hướng dẫn giải:

Khoảng cách từ A đến mặt phẳng (α) là:

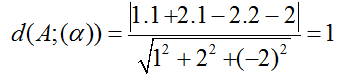
Chọn B

Ví dụ 2: Tính khoảng cách giữa hai mặt phẳng song song (α): 2x – y - 2z – 4= 0 và (β): 2x – y – 2z + 2 =0

A. 2.    B. 6.    C. 10/3    D. 4/3

Hướng dẫn giải:

Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kỳ của mặt phẳng này đến mặt phẳng kia.

Ta lấy điểm H(2; 0;0) thuộc (α) .

Khi đó

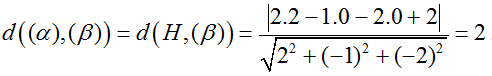
Chọn A.

Ví dụ 3: Tính khoảng cách giữa mặt phẳng (α): 2x- y – 2z – 4= 0 và đường thẳng d:

A. 1/3    B. 4/3    C. 0.    D. 2.

Hướng dẫn giải:

Đường thẳng d có vecto chỉ phương u→(1; 4; -1) mặt phẳng (α) có vecto pháp tuyến n^→(2; -1; -2)

=> Tích vô hướng u→.n→ = 1. 2+ 4.(-1) + (-1) . (-2) = 0

=> Đường thẳng d song song với mặt phẳng (α).

Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm bất kỳ của đường thẳng đến mặt phẳng.

Ta lấy điểm H(1;2;0) thuộc đường thẳng d. Khi đó:

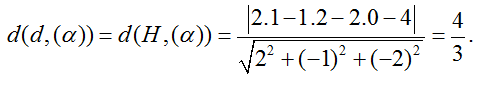
Chọn B.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): x+ 2y + 2z + m = 0 và điểm A(1; 1;1). Tìm m để khoảng cách từ điểm A đến mặt phẳng (α) bằng 1?

A. - 2    B. -8.    C. - 2 hoặc - 8 .    D. 3.

Hướng dẫn giải:

Khoảng cách từ A đến mặt phẳng (α) là:

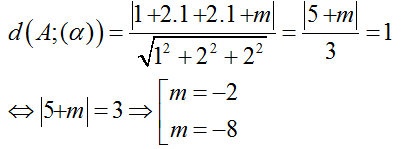
Chọn C

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, mặt phẳng (α) cắt các trục Ox; Oy; Oz lần lượt tại 3 điểm A(4; 0; 0); B(0; 3;0) và C(-2;0; 0). Khi đó khoảng cách từ gốc tọa độ O đến mặt phẳng (ABC) là

Hướng dẫn giải:

Phương trình mặt phẳng (ABC) theo đoạn chắn: x/4 + y/3 + z/(-2) = 1

Hay 3x + 4y – 6z – 12=0

Khoảng cách từ O đến mặt phẳng ( ABC) là:

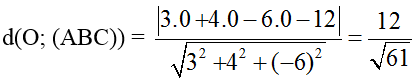
Chọn C.

Dạng 17. Viết phương trình mặt phẳng thòa mãn điều kiện T – về khoảng cách

1. Phương pháp giải

+ Khoảng cách từ điểm A( x_o; y_o; z_o ) đến mặt phẳng ( P): Ax+ By+ Cz+ D = 0 là:

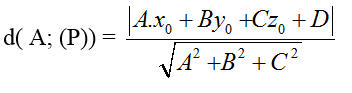
+ Muốn viết được phương trình mặt phẳng(P) cần xác định được vecto pháp tuyến n→(A; B; C) và điểm M ( x0; y0;z0 ) thuộc mặt phẳng. Khi đó; phương trình mặt phẳng cần tìm là:

A ( x- x_o) + B( y- y_o)+ C( z- z_o) =0

+ Để xác định được vecto pháp tuyến của mặt phẳng (P) ta áp dụng cách viết phương trình mặt phẳng đã được học.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng (P) qua O, vuông góc với mặt phẳng (Q): x+ y+ z- 10= 0 và cách điểm M(1; 2; –1) một khoảng bằng √2

Hướng dẫn giải:

+ Phương trình mặt phẳng (P) qua O nên có dạng: Ax+ By + Cz = 0(với A² + B² + C² > 0)

Mặt phẳng này có vecto pháp tuyến n→(A;B; C)

+ Mặt phẳng (Q) có vecto pháp tuyến n_Q→(1; 1;1)

+ Vì (P) ⊥(Q) nên: 1. A+ 1.B+ 1. C= 0 do đó; C = -A- B (1)

+ Ta có:

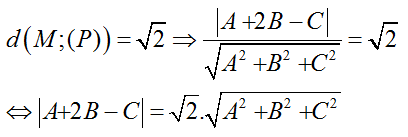
⇔ ( A+ 2B – C)² =2(A² + B² +C² ) (2)

Từ (1) và (2) ta được: 8AB + 5B2 = 0 ⇔ B = 0 hoặc 8A + 5B = 0

+ Nếu B = 0 => C = –A. Chọn A = 1, C = –1.

Khi đó phương trình mặt phẳng (P): x- z= 0

+Nếu: 8A + 5B = 0. Chọn A = 5, B = –8 => C = 3.

Khi đó phương trình mặt phẳng ( P) là: 5x- 8y+3z=0

Chọn D

Ví dụ 2: Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng Δ : 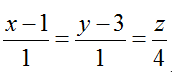và điểm M(0; –2; 0). Viết phương trình mặt phẳng (P) đi qua điểm M, song song với đường thẳng Δ, đồng thời khoảng cách d giữa đường thẳng Δ và mặt phẳng (P) bằng 4.

Hướng dẫn giải:

+ Phương trình mp (P) đi qua M(0; –2; 0) và có vecto pháp tuyến n→(a;b;c) ≠ 0 là:

a (x- 0) + b(y+ 2) + c( z-0) = 0 hay ax+ by + cz + 2b= 0

+ Đường thẳng Δ đi qua điểm A(1; 3; 0) và có một VTCP u→(1;1;4) .

Ta có đường thăng ∆ // (P) nên 1.a+ 1.b+ 4.c= 0 nên b= - a- 4c

+ Khoảng cách d giữa đường thẳng Δ và mặt phẳng (P) bằng 4 nên khoảng cách từ điểm A đến mặt phẳng (P) là 4

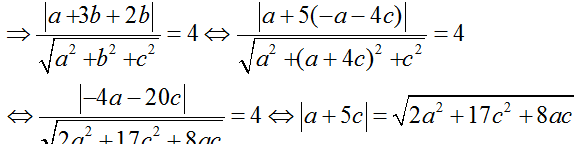
⇔ a²+ 10ac+ 25c² = 2a² + 17c² + 8ac

⇔ a² – 2ac – 8c²= 0

⇔ a = 4c hoặc a = -2c

+ Với a= 4c. Chọn a= 4; c= 1 thì b= - 8

Phương trình (P): 4x – 8y + z – 16 = 0.

+ Với a= -2c. Chọn a= 2; c= - 1thì b= 2

Phương trình (P): 2x+ 2y – z + 4= 0.

Chọn B.

Ví dụ 3: Trong không gian với hệ toạ độ Oxyz, cho đường thẳng (d): 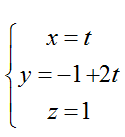và điểm A( -1; 2; 3). Mặt phẳng (P) chứa đường thẳng (d) sao cho khoảng cách từ điểm A đến mặt phẳng (P) bằng 3 có vecto pháp tuyến là:

A . n^→(2;1;-3)     B . n^→(2;1;2)    C . n^→(2;-1;-2)     D . n^→(4;-2;2)

Hướng dẫn giải:

+ Đường thẳng (d) đi qua điểm M(0; -1; 1) và có VTCT u→(1;2;0) .

Mặt phẳng (P) đi qua M(0; -1; 1) và có vecto pháp tuyến n→(a; b; c) ( với a²+ b²+ c² > 0)

Có phương trình là: a( x- 0) + b( y+1)+ c( z - 1) = 0 hay ax+ by + cz + b- c= 0 (1).

+ Do (P) chứa (d) nên: u→.n→ hay a+ 2b = 0 ⇔ a= - 2b (2)

+ Khoảng cách từ A đến ( P) là 3 nên ta có :

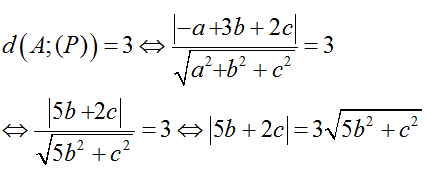
⇔ ( 5 b+ c)² = 9(5b² + c² ) ⇔ 4b² - 4bc + c² = 0

⇔ (2b – c)² = 0 ⇔ c= 2b (3)

+ Từ (2) và (3), chọn b= -1 => c= -2 và a= 2

=> PT mặt phẳng (P): 2x- y- 2z+ 1= 0 .

Vậy một vecto pháp tuyến của (P) là ( 2; -1; -2)

Chọn C

Ví dụ 4: Trong không gian với hệ toạ độ Oxyz, cho các điểm M(-1; 1; 0); N( 0;0;- 2) và I( 1; 1; 1). Mặt phẳng (P) qua M và N, đồng thời khoảng cách từ I đến (P) bằng √3 có vecto pháp tuyến là:

Hướng dẫn giải:

+ Phương trình mặt phẳng (P) nhận vecto n→(a;b;c) làm VTPT và đi qua điểm N(0; 0; -2):

ax+ by+ c( z+ 2) = 0 hay ax+ by+ cz + 2c= 0

+ Mặt phẳng ( P) đi qua điểm M(-1; 1; 0)

=> -a+ b+ 2c= 0

Suy ra: a= b+ 2c

+ Khoảng cách từ I (1; 1; 1) đến (P) bằng √3 nên :

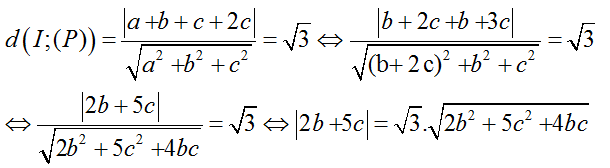
⇔ 4b²+ 20 bc+ 25c²= 6b²+ 15c²+ 12bc

⇔ 2b² – 8bc- 10c² = 0

⇔ b = 5c hoặc b = -c

+ Nếu b= 5c; chọn c= 1=> b= 5; a= 7

=> Phương trình mặt phẳng (P): 7x+ 5y+ z + 2= 0 có vecto pháp tuyến ( 7; 5; 1)

+ Nếu b= - c chọn b= 1; c= -1; a= - 1

=> Phương trình (P): - x+ y- z- 2 = 0 hay x- y+ z+ 2= 0 có vecto pháp tuyến ( 1; -1; 1)

Chọn A.

Ví dụ 5: Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD với A(1; -1; 2), B(1; 3; 0) , C(-3;4;1) và D(1;2;1). Mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C đến (P) bằng khoảng cách từ D đến (P) có vecto pháp tuyến là:

Hướng dẫn giải:

+ Phương trình mặt phẳng (P) nhận vecto n→(a;b;c) ≠ 0^→ làm VTPT và đi qua điểm A(1; -1; 2):

a(x-1)+ b(y+1)+ c( z -2) = 0 hay ax+ by+ cz – a+ b – 2c= 0

+ Mặt phẳng ( P) đi qua điểm B(1; 3; 0)

=> a+ 3b – a+ b – 2c= 0 hay 4b – 2c= 0

Suy ra: c= 2b

+ Khoảng cách từ C( -3; 4; 1) đến (P) bằng khoảng cách từ D(1; 2;1) đến (P) nên :

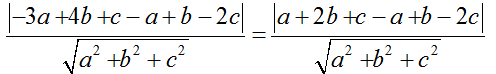
⇔ | - 4a + 5b – c| = | 3b – c |

⇔ | -4a + 5b- 2b| = | 3b – 2b |

⇔ | - 4a + 3b| = | b |

⇔ 16a² – 24 ab+ 9b² = b²

⇔ 16a² – 24ab + 8b² = 0

+ Với b= a; chọn a= l=> b =1; c= 2

Phương trình mặt phẳng (P) : x+ y+ 2z - 4= 0 có vecto pháp tuyến (1; 1; 2)

+ Với chọn b=2; a= 1 => c = 4

=> Phương trình mặt phẳng (P) là : x+ 2y+ 4z - 7= 0 có vecto pháp tuyến là( 1; 2; 4)

Chọn A.

Dạng 18.Vị trí tương đối của hai mặt phẳng

1. Phương pháp giải

Trong không gian Oxyz, cho hai mặt phẳng (α): A₁x+ B₁y+ C₁z + D₁ = 0 và (β):

A₂x+ B₂y+ C₂z + D₂= 0

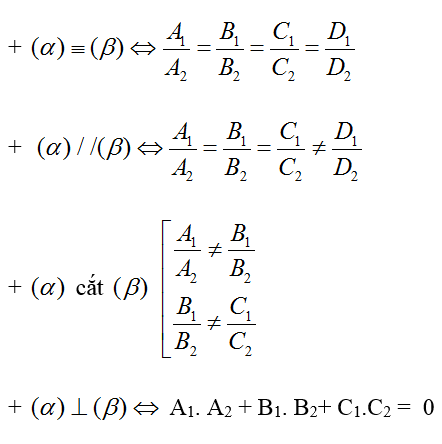
2. Ví dụ minh họa

Ví dụ 1: Trong không gian Oxyz, cho mặt phẳng (P): x- 3y + 2z + 11 = 0 và (Q): ( 2m - 1)x + m(1– 2m)y + (2m – 4)z - 9= 0 .Với giá trị nào của m thì (P) và (Q) vuông góc với nhau

A. m= 1 hoặc m= 2    B. m= 1 hoặc m = -3/2

C. m= -1 hoặc m= 3/2    D . m= 2 hoặc m = 1/2

Hướng dẫn giải:

Mặt phẳng (P) có vecto pháp tuyến n₁→( 1; -3; 2)

Mặt phẳng (Q) có vecto pháp tuyến n₂→(2m- 1; m(1- 2m); 2m- 4)

Mặt phẳng (P) và (Q) vuông góc với nhau khi và chỉ khi:

n₁→.n₂→ = 0

⇔ 1.(2m- 1) -3m(1 – 2m)+ 2(2m – 4) = 0

⇔ 6m² + 3m – 9 = 0

⇔ m = 1 hoặc m = -3/2

Chọn B

Ví dụ 2: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): x+ 2y- 4z+ 1= 0 và mặt phẳng (Q) đi qua ba điểm A(1; 0; 0); B(0; 3; 0) và C(0; 0; -4). Xác định vị trí tương đối của hai mặt phẳng (P) và (Q)?

A. Song song    B. Cắt nhau nhưng vuông góc

C. Trùng nhau    D. Cắt nhau nhưng không vuông góc

Hướng dẫn giải:

+ Phương trình mặt phẳng (Q): x/1 + y/3 + z/(-4) = 1 hay 12 x+ 4y – 3z – 12= 0

+ Ta có: 1/12 ≠ 2/4 nên hai mặt phẳng này cắt nhau.

Hai mặt phẳng (P) và (Q) có hai vecto pháp tuyến lần lượt là n₁→(1; 2; -4); n₂→( 12; 4; -3)

Tích vô hướng: n₁→.n₂→ = 1. 12+ 2. 4 + (-4). (-3)= 32

=> Hai mặt phẳng đã cho cắt nhau nhưng không vuông góc

Chọn D.

Ví dụ 3: Trong không gian Oxyz, mặt phẳng (P) đi qua điểm M (0; 1; 2) và song song với mặt phẳng (Q): 2x – 4y + 12= 0. Mặt phẳng (R) có phương trình: 4x- 8y+ 10z - 9= 0. Xác định vị trí tương đối của mặt phẳng (P) và (R)

A. Cắt nhau nhưng vuông góc    B. Trùng nhau

C. Cắt nhau nhưng không vuông góc    D. Song song

Hướng dẫn giải:

Mặt phẳng (P) song song với mặt phẳng (Q) nên VTPT của mặt phẳng (Q) là n→(2; -4; 0)

Mặt phẳng (P) đi qua điểm M(0; 1; 2) và có VTPT n→(2; -4; 0) nên có phương trình là:

2( x- 0) – 4( y- 1) + 0(z – 2) = 0

⇔ 2x – 4y + 4= 0 hay x- 2y + 2 = 0

+ Ta có: 1/4 ≠ 0/10 nên hai mặt phẳng (P) và (R) cắt nhau.

Hai mặt phẳng (P) và (R) có hai vecto pháp tuyến lần lượt là n₁→(1; -2; 0) và n₂→( 4; - 8; 10)

Tích vô hướng n₁→. n₂→= 1.4 + (-2).(-8) + 0.10 = 20

=> Hai mặt phẳng đã cho cắt nhau nhưng không vuông góc

Chọn C.

Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz; cho hai mặt phẳng (P): x+ 2y- z+ 10= 0 và (Q): 2x+ my – nz+ 20= 0. Xác định m và n để hai mặt phẳng (P) và (Q) trùng nhau?

A. m= 2 và n= 1    B. m= -4 và n= 2

C. m= 2 và n= 2    D. m= 4 và n= 2

Hướng dẫn giải:

+ Để hai mặt phẳng (P) và (Q) trùng nhau thì:

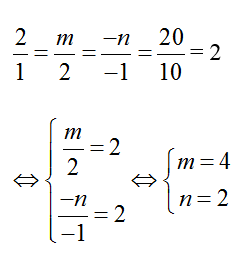
Chọn D.

Ví dụ 5: Trong không gian với hệ trục tọa độ Oxyz; cho hai mặt phẳng (P): 2x- y+ 3z -9= 0 và (Q): 6x + my – nz + 12= 0. Tìm m và n để hai mặt phẳng (P) và (Q) song song với nhau

A. m= 3; n= -9    B. m= -3; n = -9

C. m= -3; n= 9    D. Đáp án khác

Hướng dẫn giải:

Để hai mặt phẳng (P) và (Q) song song với nhau thì:

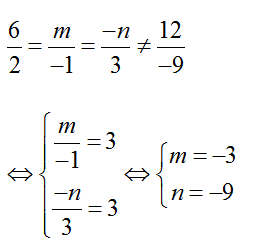
Chọn B.

Dạng 19. Vị trí tương đối giữa mặt phẳng và mặt cầu

1. Phương pháp giải

Trong không gian Oxyz, cho mặt phẳng (P): Ax + By + Cz + D = 0 và mặt cầu

(S): (x- a)² + (y – b)² + (z- c)² = R²

Để xét vị trí tương đối của (P) và (S) ta làm như sau:

Bước 1: Tính khoảng cách d từ tâm I của (S) đến mặt phẳng (P)

Bước 2:

+ Nếu d > R thì (P) không cắt (S).

+ Nếu d = R thì (P) tiếp xúc với (S) tại H, khi đó H được gọi là tiếp điểm, là hình chiếu vuông góc của I lên mặt phẳng (P), mặt phẳng (P) được gọi là tiếp diện.

+ Nếu d < R thì (P) cắt (S) theo đường tròn có phương trình:

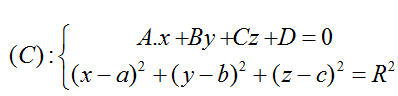
Bán kính của (C) là

Tâm J của (C) là hình chiếu vuông góc của I trên (P)

2. Ví dụ minh họa

Ví dụ 1: Cho mặt phẳng (P): 2x – y + 2z - 5 = 0 và (S): (x- 3)² + y² + ( z- 4)² = 9. Tìm mệnh đề đúng

A. Mặt phẳng và mặt cầu cắt nhau

B. Mặt phẳng và mặt cầu tiếp xúc nhau và tọa độ tiếp điểm là (1; 1; 2)

C. Mặt phẳng và mặt cầu không cắt nhau

D. Mặt phẳng và mặt cầu tiếp xúc nhau tại điểm (2; -1; 2)

Hướng dẫn giải:

Mặt cầu (S) có tâm I (3; 0; 4) và bán kính R = 3.

Mặt phẳng (P) có vecto pháp tuyến n→(2; -1; 2)

Khoảng cách từ tâm I đến mặt phẳng (P) là:

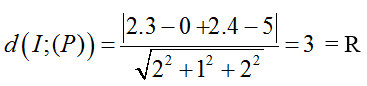
Do đó, mặt phẳng (P) và mặt cầu (S) tiếp xúc với nhau.

Gọi M(a; b; c) là tọa độ tiếp điểm của (P) và (S)

=> IM^→( a- 3; b; c - 4)

Do IM vuông góc với mặt phẳng (P) nên ta có: IM→ = k.n→

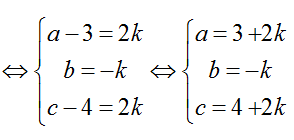
Lại có M thuộc mặt phẳng (P) nên ta có:

2(2k+ 3) – (- k)+ 2.( 4+ 2k) -5 = 0 hay 9k+ 9 = 0⇔ k= -1

Khi đó, M( 1, 1, 2)

Vậy tọa độ tiếp điểm là (1; 1; 2)

Chọn B.

Ví dụ 2: Trong không gian với hệ trục tọa độ Oxyz; cho mặt phẳng (P). x- 2y- 3z+ 11= 0 và mặt cầu ( S): x²+ y² + z² – 4x+ 4y - 2z + m= 0. Tìm m để mặt phẳng (P) tiếp xúc với mặt cầu (S)

A. m= 1    B. m = -3    C. m= - 5     D. m = 3

Hướng dẫn giải:

+ Mặt cầu (S) có tâm I(2; -2; 1) và bán kính

( điều kiện m < 9)

+ Khoảng cách từ tâm I đến mặt phẳng (P):

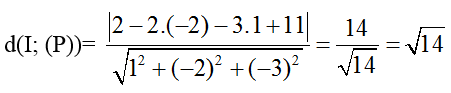
+ Để mặt phẳng (P) tiếp xúc với mặt cầu thì:

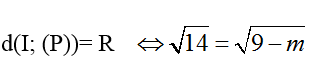
⇔ 14= 9- m nên m= -5

Chọn C.

Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz; cho mặt phẳng (P): 4x- 2y- 4z + 6= 0 và mặt cầu (S): (x-2)²+ ( y+ 2)² + z² = 25. Tìm mệnh đề đúng?

A. Mặt phẳng (P) tiếp xúc với mặt cầu tại điểm (2; -3; 1)

B. Mặt phẳng (P) cắt đường tròn theo một đường tròn có tâm (0; 1; 2)

C. Mặt phẳng (P) tiếp xúc với mặt cầu tại điểm (0; -1; 3)

D. Mặt phẳng (P) cắt đường tròn theo một đường tròn có tâm ( 0; -1; 2)

Hướng dẫn giải:

+ Mặt cầu (S): có tâm I(2; -2; 0) và bán kính R= 5

+ Mặt phẳng (P) có vecto pháp tuyến n→( 4; -2; - 4)

+ Khoảng cách từ tâm I đến mặt phẳng (P):

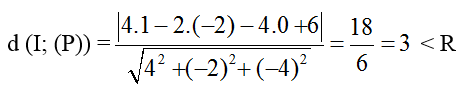
=> Mặt phẳng (P) và mặt cầu (S) cắt nhau theo một đường tròn

Gọi J (a; b; c) là tọa độ tâm của đường tròn (C)

Ta có: IJ→( a - 2; b+2; c)

Do IJ vuông góc với mặt phẳng (P) nên IJ→ = kn→

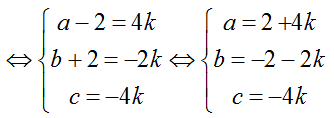
Lại có J thuộc mặt phẳng (P)

=> 4( 4k+ 2) – 2.(- 2- 2k) – 4 ( -4k) + 6= 0

⇔ 16k + 8 + 4 + 4k + 16k + 6= 0

⇔ 36k+ 18= 0 ⇔ k = -1/2

Vậy tâm J(0; - 1; 2)

Chọn D.

Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz; cho mặt phẳng (P): 2x- y- 2z+ 10= 0 và mặt cầu (S): (x- 1)² + ( y- 2)² + ( z+ 1)² = R². Biết mặt phẳng (P) cắt mặt cầu (S) theo đường tròn có bán kính r = 2. Tìm R

A. 2√5    B. 5     C. 2√15     D. 3√5

Hướng dẫn giải:

+ Mặt cầu (S) có tâm I( 1;2; -1) và bán kính R.

+ Khoảng cách từ tâm I đến mặt phẳng (P):

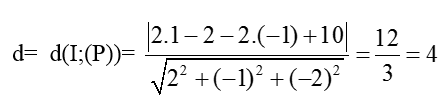
+ Để mặt phẳng (P) cắt mặt cầu ( S) theo đường tròn có bán kính r= 2 thì:

R² = d² + r² = 4² + 2² = 20

=> R= 2√5

Chọn A.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): - 2x + y- 6z+ m= 0 và mặt cầu ( S) : (x- 1)² +( y+ 2)² + (z+ 3)² = 41. Tìm điều kiện của m để mặt phẳng (P) và mặt cầu ( S) có điểm chung

A. – 55 < m < 27    B. -55 ≤ m ≤ 27

C. m < -55; m > 27    D. m ≤ -55; m ≥ 27

Hướng dẫn giải:

+ Mặt cầu ( S) có tâm I(1; -2; -3) và bán kính R= √41

+ Khoảng cách từ tâm I đến mặt phẳng (P):

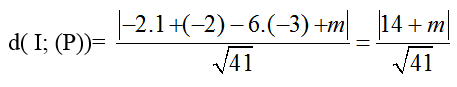
+ Để mặt phẳng (P) và mặt cầu (S) có điểm chung thì:

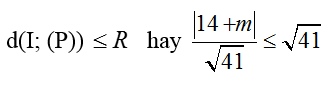
⇔ |14+ m| ⇔ 196 + 28m + m² ≤ 1681

⇔ m² + 28m – 1485 ≤ 0 ⇔ - 55 ≤ m ≤ 27

Chọn B

Dạng 20. Xác định góc giữa hai mặt phẳng

1. Phương pháp giải

Trong không gian Oxyz, cho hai mặt phẳng (P): A₁x + B₁y + C₁z+D₁ = 0 và (Q): A₂x + B₂y +C₂z +D₂ = 0. Góc giữa hai mặt phẳng (P) và (Q) bằng hoặc bù với góc giữa hai vecto pháp tuyến n_P^→ và n_Q^→

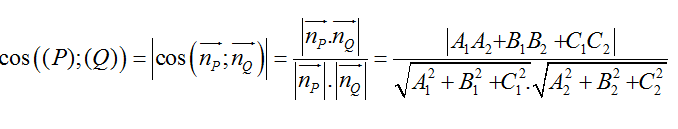
2. Ví dụ minh họa

Ví dụ 1: Trong không gian với hệ toạ độ Oxz, tính góc hợp bởi mặt phẳng (α): √2x+ y – 5= 0 và mặt phẳng (Oxy)

A. 30^o     B. 90^o     C. 45^o     D. 60^o

Hướng dẫn giải:

Mặt phẳng (α) có vecto pháp tuyến n₁→(√2;1;0)

Mặt phẳng (Oxy) có phương trình z = 0 nên có vecto pháp tuyến n₂→(0; 0; 1)

Góc giữa hai mặt phẳng (α) và (Oxy) là:

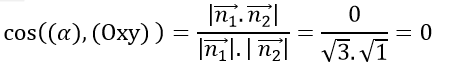
Vậy góc giữa mặt phẳng (α) và (Oxy) là 90^o.

Chọn B.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, gọi (P) là mặt phẳng chứa trục Oy và tạo với mặt phẳng (Q): y + z + 1= 0 góc 60^o. Phương trình mặt phẳng (P) là:

A. x- y= 0 hoặc y= 0    B. x- z= 0 hoặc x+ z= 0

C. y+ z= 0 hoặc x+ y= 0    D. x- z= 0 hoặc x- y= 0

Hướng dẫn giải:

Giả sử phương trình mặt phẳng (P) có dạng: Ax+ By + Cz + D = 0

Đường thẳng Oy đi qua điểm O(0; 0; 0) và có vecto chỉ phương u→(0; 1; 0)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→(0;1; 1)

Mặt phẳng (P) chứa đường thẳng (d) nên u→.n_Q→ = 0 ⇔ B = 0

Lại có mặt phẳng (P) tạo với mặt phẳng (Q) một góc bằng 60^o nên ta có:

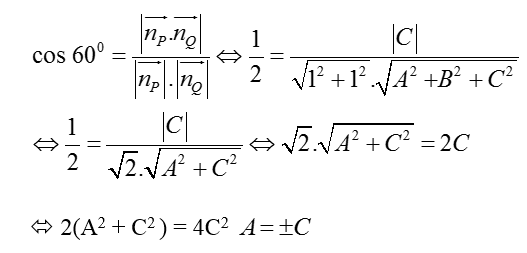
Chọn C= 1 , ta có A = ±1

Khi đó, phương trình mặt phẳng (P) đi qua O(0; 0; 0) và có vecto pháp tuyến n_P→(A;B;C) là x+ z = 0 hoặc –x + z= 0

Chọn B.

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): x+ y- 10= 0 và mặt phẳng ( Q): x + mz +19= 0. Xác định m để góc giữa hai mặt phẳng (P) và (Q) bằng 45^o?

A. m= 0    B. m = 1    C. m = -2     D. m= 3

Hướng dẫn giải:

+ Mặt phẳng (P) có vecto pháp tuyến là n→(1;1;0)

+ Mặt phẳng (Q) có vecto pháp tuyến là n'→(1;0;m)

+ Để góc giữa hai mặt phẳng (P) và (Q) bẳng 45^o thì:

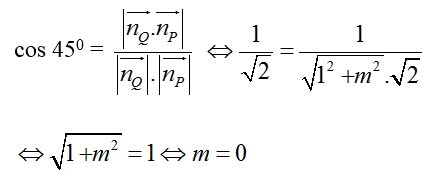
Chọn A.

Ví dụ 4: Trong không gian Oxyz, mặt phẳng (P) đi qua ba điểm A(1; -2; 0), B(1; 1; 1) và C(0; 1; -2). Mặt phẳng (Q) có phương trình: 2x+ y- 4z+ m=0 . Xác định cosin góc tạo bởi hai mặt phẳng (P) và (Q)

Hướng dẫn giải:

+ Xác định vecto pháp tuyến của mặt phẳng (P):

Ta có: AB→(0; -3; 1); AC→( -1; - 3; -2)

[AB→;AC→] = ( 9; -1; -3)

Gọi n→ là một VTPT của mặt phẳng (P) ta có 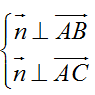nên n^→ cùng phương với [AB^→;AC^→]

Chọn n→( 9; -1; -3) ta được vecto pháp tuyến của mặt phẳng (P)

+ Vecto pháp tuyến của mặt phẳng (Q) là n'→(2; 1;- 4).

+ Cosin góc tạo bởi hai mặt phẳng (P) và ( Q) là

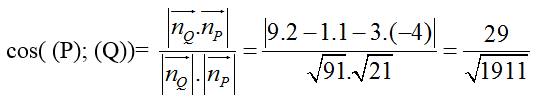
Chọn D.

Ví dụ 5: Trong không gian hệ tọa độ Oxyz, gọi mặt phẳng (P) chứa đường thẳng d: 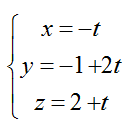và vuông góc với mặt phẳng (Q): x+ 2y – z + 1 = 0. Mặt phẳng (R) có phương trình: 2x+ my+ z – 9= 0 . Xác định m để cos( (P); (R))= 3/√12

A.m = ±2     B. m = ±1     C. m = ±3     D. m= 0

Hướng dẫn giải:

+ Xác định vecto pháp tuyến của mặt phẳng (P):

Đường thẳng d đi qua điểm A (0; -1; 2) và có vecto chỉ phương u→( -1; 2; 1)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→(1; 2; -1)

Mặt phẳng (P) chứa đường thẳng d và vuông góc với (Q) nên (P) có một vecto pháp tuyến là

[u→;n_Q→] = ( - 4; 0; -4) chọn n_P→(1; 0; 1)

+ Mặt phẳng (R) có vecto pháp tuyến là: n_R→( 2 ;m;1)

Theo đầu bài ta có; cos( (P); (R)) = 3/√12

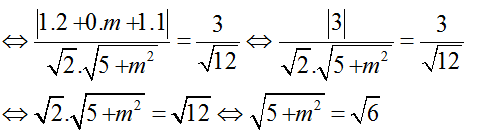
⇔ 5+ m² = 6

⇔ m² = 1 nên m= 1 hoặc m = -1

Chọn B.

Dạng 21. Viết phương trình mặt phẳng (P) chứa một đường thẳng (d) và tạo với mặt phẳng (Q): Ax+ By + Cz + D = 0 một góc Φ cho trước.

1. Phương pháp giải

• Tìm vecto pháp tuyến của (Q) là n_Q→, vecto chỉ phương của (d) là u→

• Gọi vecto pháp tuyến của (P) là n_P→

Dùng phương pháp vô định giải hệ

• Áp dụng cách viết phương trình đi qua một điểm và có 1 vecto pháp tuyến.

2. Ví dụ minh họa

Ví dụ 1: Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (Q): x+ 2y + z - 3= 0 và đường thẳng d: 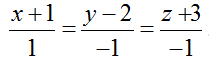. Viết phương trình mặt phẳng (P) chứa (d) và hợp với mặt phẳng (Q) một góc α thỏa mãn cosα = √3/6

A. y- z+ 3= 0    B. 5x- 3y + 8z- 10= 0

C. 2x- 3y+ 5z- 10= 0    D. Đáp án khác

Hướng dẫn giải:

Giả sử phương trình mặt phẳng (P) có dạng: Ax+ By + Cz + D = 0 (A² + B² + C² > 0) nhận vectơ n^→( A;B; C) làm vecto pháp tuyến.

Đường thẳng d đi qua điểm M(-1; 2; -3) và có vecto chỉ phương u→(1; -1; -1)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→(1; 2; 1)

Mặt phẳng (P) chứa đường thẳng (d) nên u→.n_Q→ = 0

⇔ A- B – C= 0 ⇔ C = A – B

Lại có mặt phẳng (P) tạo với mặt phẳng (Q) một góc góc α thỏa mãn cosα = √3/6

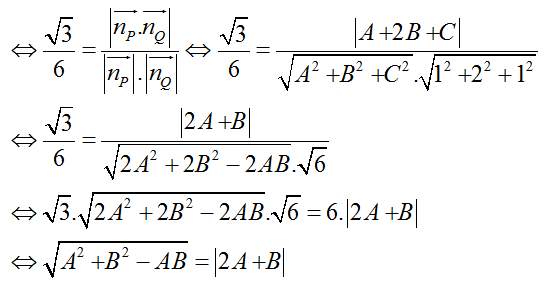
⇔ A²+ B² - AB = 4A²+ 4AB + B²

⇔ 3A² + 5AB = 0

+ Với A = 0, chọn B = 1 thì C= - 1

Mặt phẳng (P) đi qua M(-1; 2; -3) và nhận vecto ( 0; 1; -1) làm vecto pháp tuyến

=> Phương trình mp (P): 0( x+ 1) + 1( y - 2) – 1( z+ 3) = 0 hay y - z – 5= 0

+ Với 3A = - 5B; chọn B = - 3 => A= 5; C= 8

Khi đó, phương trình mặt phẳng (P) đi qua M(-1; 2; -3) và có VTPT n_P→(5; -3; 8) là:

5( x+ 1) – 3( y- 2) + 8( z+ 3) = 0 hay 5x – 3y + 8z + 35= 0

Chọn D.

Ví dụ 2: Trong không gian hệ tọa độ Oxyz, cho đường thẳng d có phương trình (d): 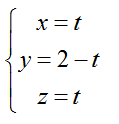và mặt phẳng (Q): x + 2y + z – 5= 0 . Viết phương trình mặt phẳng (P) chứa (d) và hợp với (Q) một góc 30^o.

A. x+ y- 2= 0 hoặc x+ z – 2= 0

B. x+ y - 2= 0 hoặc y+ z - 2= 0

C. y+ z - 2= 0 hoặc x – z - 2= 0

D. Đáp án khác

Hướng dẫn giải:

Giả sử phương trình mặt phẳng (P) có dạng: Ax+ By + Cz + D = 0 nhận vecto n_P→(A; B; C) làm vecto pháp tuyến.

Đường thẳng (d) đi qua điểm M(0; 2; 0) và có vecto chỉ phương u→(1; -1; 1)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→(1 ; 2;1)

Mặt phẳng (P) chứa đường thẳng (d) nên u→.n_P→ = 0

^→ A- B+ C = 0 ⇔ C = B - A

Lại có mặt phẳng (P) tạo với mặt phẳng (Q) một góc bằng 30^o nên ta có:

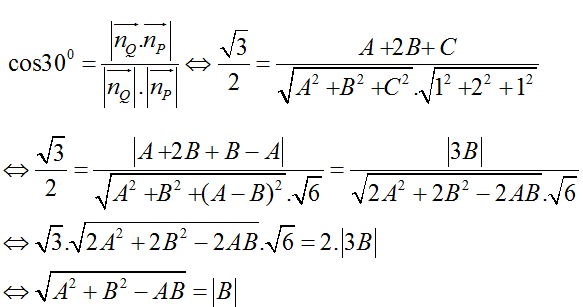
⇔ A² + B² – AB= B²

^→ A² – AB = 0

+ Với A = 0, chọn B = 1; C = 1.

Mặt phẳng ( P) đi qua M(0; 2; 0) và nhận vecto (0;1; 1) làm vecto pháp tuyến:

0(x - 0) + 1( y - 2) +1.( z - 0) = 0 hay y+ z - 2 = 0

+ Với A = B , chọn A= B = 1 C = 0

Khi đó, phương trình mặt phẳng (P) đi qua M(0; 2; 0) và có VTPT n_P→(1; 1;0) là:

1( x- 0) + 1( y-2) + 0( z- 0) = 0 hay x+ y- 2= 0

Chọn B

Ví dụ 3: Cho mặt phẳng (α): 3x- 2y + 2z – 5= 0. Điểm A( 1; -2; 2). Có bao nhiêu mặt phẳng đi qua A và tạo với mặt phẳng (α) một góc 45^o

A. Vô số.    B. 1.    C. 2.    D. 4.

Hướng dẫn giải:

Gọi n_β→(a; b;c) là vectơ pháp tuyến của mặt phẳng (β) cần lập.

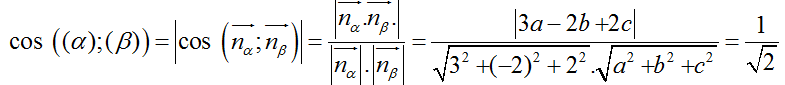
=> 2( 3a – 2b + 2c)² = 17 (a² + b²+ c²)

⇔ a² - 9b² – 9c² - 12ab – 8bc + 12ac = 0

Phương trình trên có vô số nghiệm.

Suy ra có vô số vectơ n_β→(a; b; c) là véc tơ pháp tuyến của (β)

Suy ra có vô số mặt phẳng (β) thỏa mãn điều kiện bài toán

Chọn A.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz cho điểm M(1; 0;0) và N(0; 0; -1).Mặt phẳng (P) qua điểm M; N và tạo với mặt phẳng (Q): x- y- 4= 0 một góc bằng 45^o. Phương trình mặt phẳng (P) là

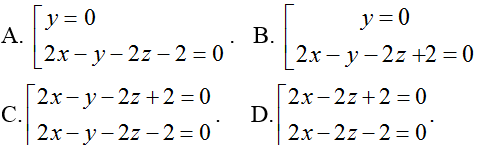
Hướng dẫn giải:

+ Mặt phẳng (Q) có vecto pháp tuyến là n_Q→(1; -1; 0)

+ Mặt phẳng (P) đi qua M(1; 0; 0) và vectơ pháp tuyến n→(a; b; c) với a²+ b² +c² > 0 có phương trình là:

a( x - 1) + b(y - 0) + c( z - 0) = 0 hay ax + by+ cz – a= 0

+ Mặt phẳng (P) đi qua điểm N( 0; 0; -1) nên :

a.0+ b.0+ c.(-1) - a= 0 hay –c - a= 0 ⇔ c = -a

+ Hai mặt phẳng (P) và (Q) hợp nhau góc 45^o nên :

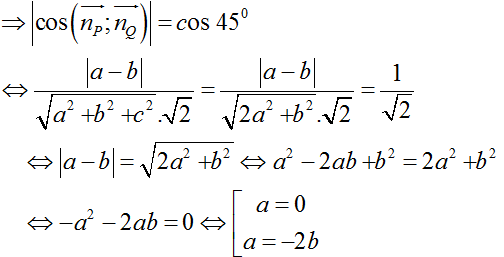
+ Với a= 0 => c= 0; chọn b= 1

Mặt phẳng (P)đi qua M( 1; 0; 0 ) vecto pháp tuyến (0; 1; 0) nên phương trình (P): y= 0

+ Với a= -2b chọn b= -1 suy ra a= 2

mặt phẳng đi qua M( 1; 0; 0) và vecto pháp tuyến ( 2; -1;-2)

=> Phương trình ( P): 2( x - 1) – 1( y - 0) – 2( z - 0) = 0 hay 2x – y - 2z - 2= 0

Vậy có hai mặt phẳng thỏa mãn là : z = 0 và 2x- y- 2z – 2= 0

Chọn A.

Ví dụ 5: Trong không gian với hệ trục toạ độ Oxyz; cho điểm M( 0; -1; 2) ; N( -1; 1; 3). Gọi (P) là mặt phẳng đi qua M; N và tạo với mặt phẳng (Q): 2x – y – 2z – 2= 0 góc có số đo nhỏ nhất. Điểm A( 1;2; 3) cách mp (P) một khoảng là

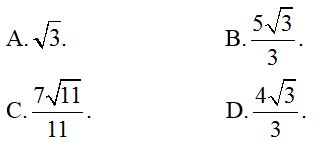
Hướng dẫn giải:

+ Mặt phẳng (Q) có vecto pháp tuyến là : n_Q→(2; -1; -2)

+ Gọi vecto pháp tuyến của mặt phẳng (P) là : n_P→(a; b;c) ( a²+ b²+ c² > 0)

+ Mặt phẳng (P) có VTPT n^→ vuông góc với MN→(-1; 2; 1) nên

-1.a+ 2b+ 1.c= 0 ⇔ a= 2b+ c

=> Vecto pháp tuyến của mặt phẳng ( P) là : n_P^→(2b+c; b;c)

+ Gọi α là góc tạo bởi (P) và ( Q) , α nhỏ nhất khi cosα lớn nhất.

Ta có

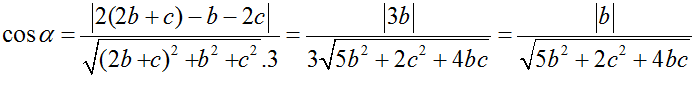
+ Nếu b=0 thì cosα= 0

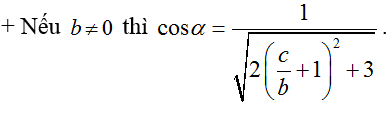
Khi đó, cos α lớn nhất khi và chỉ khi 2(c/b + 1)² +3 nhỏ nhất

=> c/b = -1 chọn b = 1=> c= -1 và a= 2b+ c= 1

Vậy mặt phẳng (P) đi qua M( 0; -1; 2) vecto pháp tuyến ( 1; 1; -1) có phương trình là

1( x- 0) +1(y+ 1) - 1(z- 2) = 0 hay x+ y- z + 3= 0.

Do đó

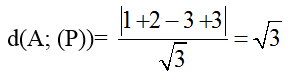
Chọn A.