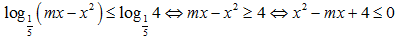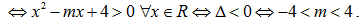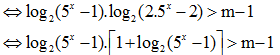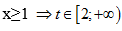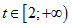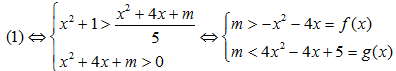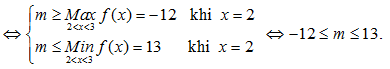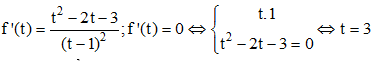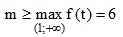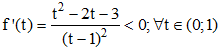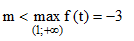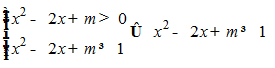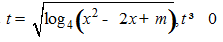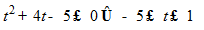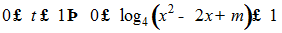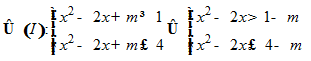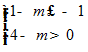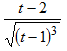Cách giải bất phương trình logarit có chứa tham số m cực hay - Toán lớp 12

---

Cách giải bất phương trình logarit có chứa tham số m cực hay

Với Cách giải bất phương trình logarit có chứa tham số m cực hay Toán lớp 12 tổng hợp 7 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải bất phương trình logarit có chứa tham số m từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1:Gọi S là tổng tất cả giá trị nguyên của tham số m (m<3) để bất phương trình 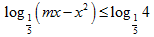vô nghiệm. Tính S.

   A. S= - 3

   B.S= -7

   C. S=0

   D. S= 4

Lời giải:

   

   Để bất phương trình đã cho vô nghiệm thì bất phương trình x2- mx+4≤0 vô nghiệm

   

   Mà m nguyên và m< 3 nên m= -3; -2; -1; 0;1; 2

   Khi đó S = -3.

    Chọn A.

Câu 2:Tìm tất cả các giá trị thực của tham số m để bất phương trình 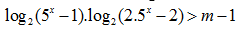có nghiệm x≥1?

   A. m≥7

   B.,m> 7

   C. m≤7

   D.m < 7

Lời giải:

   Bất phương trình đã cho

   

   Đặt 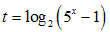do x≥1

   Bất phương trình đã cho tương đương với t(1+t)> m-

   Suy ra t²+ t>m-1 hay f(t) > m-1

   Với f(t) = t²+ t

   Đạo hàm f’ (t) = 2t+1>0 với nên hàm đồng biến trên

   Nên Min f(t) =f(2) =6

   Do đó để để bất phương trình 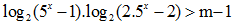có nghiệm x≥1 thì: m-1≤min f(t) hay m≤7

    Chọn C.

Câu 3:Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình .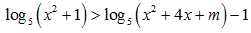

   A. .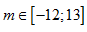

   B. .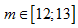

   C. .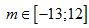

   D. .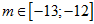

Lời giải:

   

   Hệ trên thỏa mãn với mọi 2<x< 3

   

    Chọn A.

Câu 4:Bất phương trình lg²x-mlg x+m+3≤0 có nghiệm x > 1 khi giá trị của m là:

   A. .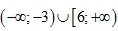

   B. .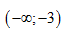

   C. .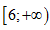

   D. (3;6].

Lời giải:

   Điều kiện mx> 1

   Đặt t= lg x, với x> 1 thì lg x> 0

   Khi đó phương trình đã cho trở thành t2- mt+m+3≤0 hay t2+ 3≤ m(t-1) (*)

   TH1: Với t-1> 0 hay t> 1 Khi đó (*) 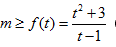(I)

   Xét hàm số. với t> 1, có

   Suy ra 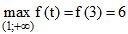. Khi đó để (I) có nghiệm khi

   TH2: Với t<1 khi đó (*) 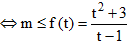(II)

   Xét hàm số 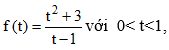với 0< t<1, có

   Suy ra 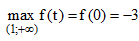. Khi đó để (I) có nghiệm khi

   Vậy 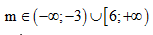là giá trị cần tìm của bài toán.

    Chọn A.

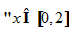
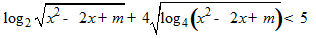
Câu 5:Tìm m để thỏa mãn BPT

   A. 2≤m< 4

   B.2< m< 4

   C. m≥2

   D. m< 4

Lời giải:

   Điều kiện:

   Đặt

   BPT có dạng:

   Vì t≥0 nên ta được

   Vậy BPT

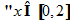
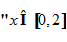
   BPT có nghiệm với khi và chỉ khi hệ (I) có nghiệm với .

   Khi mỗi BPT trong hệ (I) có nghiệm với .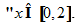

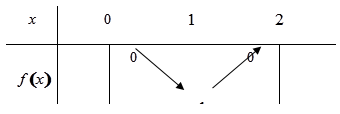
   Xét hàm số f(x) =x²- 2x ta có bảng biến thiên

   

   Từ bảng biến thiên ta suy ra

   Hay . 2≤m< 4

    Chọn A.

Câu 6:Xác định m để bất phương trình 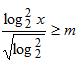(1) có nghiệm đúng với mọi m > 0.

   A. m≤1

   B.m ≤2

   C. m< 1

   D. m > 2

Lời giải:

   Đặt t= 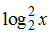, điều kiện t > 1

   Khi đó (1) có dạng: y = 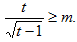(2)

   Vậy (1) nghiệm đúng với ∀ m > 0 ⇔ (2) nghiệm đúng với ∀ t >1.

   Xét hàm số: y = .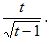

   Tập xác định D = (1, +∞ ).

   Đạo hàm: y’ =

   Y’ =0 khi t-2=0 hay t= 2

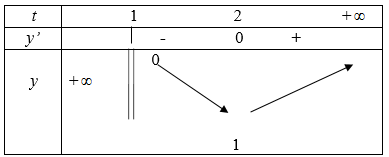
   Bảng biến thiên:

   

   Vậy bpt nghiệm đúng với ∀ t >1 ⇔ m 1.

    Chọn A.

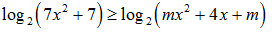
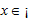
Câu 7:Với giá trị nào của m thì bất phương trình nghiệm đúng với mọi ?

   A. 2< m≤5

   B. 2< m< 7

   C.5 ≤ m ≤ 9

   D. m ≥ 9 .

Lời giải:

   Ta phải có 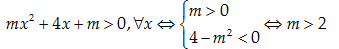(1).

   Đồng thời

    (2).

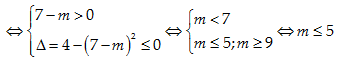
   Từ (1) và (2) suy ra chọn đáp án 2< m≤5.

    Chọn A.