Tất tần tật về tính thể tích khối đa diện và cách giải

Tất tần tật về tính thể tích khối đa diện và cách giải

Với Tất tần tật về tính thể tích khối đa diện và cách giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về tính thể tích khối đa diện từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

I. LÝ THUYẾT

Thể tích của mỗi khối đa diện (H) là một số dương V_(H) thỏa mãn các tính chất sau:

a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V_(H) = 1

b) Nếu hai khối đa diện (H₁) và (H₂) bằng nhau thì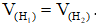

c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H₁) và (H₂) thì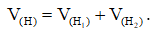

Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.

II. PHƯƠNG PHÁP

1) Phương pháp tính toán trực tiếp:

Bước 1: Xác định và tính chiều cao của khối đa diện

Bước 2: Tìm diện tích đáy bằng các công thức

Bước 3: Sử dụng công thức tính thể tích.

Một số dạng toán cụ thể:

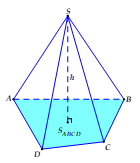
Dạng 1: Thể tích khối chóp

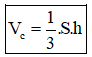
Với: S: Diện tích đáy khối chóp.

h: Chiều cao khối chóp.

Ví dụ 1: Cho khối chóp có đáy là hình vuông cạnh a và chiều cao 4a. Thể tích của khối chóp đã cho bằng

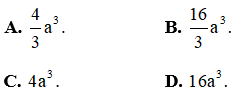
Hướng dẫn giải

Vì đáy là hình vuông cạnh a nên diện tích đáy hình chóp là: S = a² .

Chiều cao của hình chóp là h = 4a.

Vậy thể tích khối chóp là: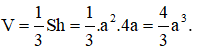

Chọn A.

Dạng 2: Thể tích khối lăng trụ

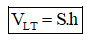
Với S: Diện tích đáy lăng trụ.

h: Chiều cao lăng trụ.

Ví dụ 2: Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối lăng trụ đã cho bằng

Hướng dẫn giải

Vì đáy là hình vuông cạnh a nên ta có diện tích đáy là S = a².

Chiều cao của lăng trụ là h = 2a.

Vậy thể tích khối lăng trụ là: V = Sh = a².2a = 2a³.

Chọn C.

Dạng 3: Thể tích khối hộp chữ nhật:

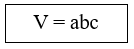
với a, b, c lần lượt là ba kích thước của hình hộp chữ nhật.

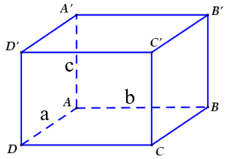
Ví dụ 3: Thể tích khối hộp chữ nhật ABCD. A’B’C’D’ có các cạnh AB = 3, AD = 4, AA’ = 5 là

A. V = 30.

B. V = 60.

C. V = 10.

D. V = 20.

Hướng dẫn giải

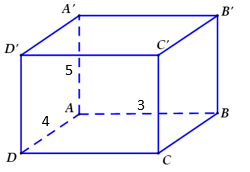
Ta có 3 kích thước của hình hộp chữ nhật đã cho lần lượt là 3, 4, 5.

Khi đó thể tích khối hộp chữ nhật là:

V = 3.4.5 = 60.

Chọn B.

Dạng 4: Thể tích khối lập phương:

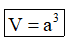
Trong đó a là độ dài cạnh hình lập phương.

Ví dụ 4 : Tính thể tích của khối lập phương có cạnh bằng 2.

Hướng dẫn giải

Thể tích khối lập phương có cạnh bằng 2 là: V = 2³ = 8 (đvtt).

2) Phương pháp tính thể tích gián tiếp bằng cách phân chia các khối đa diện.

Trong nhiều trường hợp, việc tính trực tiếp thể tích khối đa diện bằng phương pháp trực tiếp gặp khó khăn vì hai lí do: khó xác định và tính được chiều cao hoặc khó tính được diện tích đáy. Khi đó, ta có thể làm theo các phương pháp tính thể tích gián tiếp.

Bước 1: Ta chia khối đa diện thành nhiều khối đa diện nhỏ mà có thể tính thể tích của chúng.

Bước 2: Sau đó, ta cộng các kết quả lại, ta sẽ có kết quả cần tìm.

Ví dụ minh họa: Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước là 2cm, 3cm, 6cm. Thể tích của khối tứ diện ACB’D’ bằng

A. 8cm³

B. 12cm³

C. 6cm³

D. 4cm³

Hướng dẫn giải:

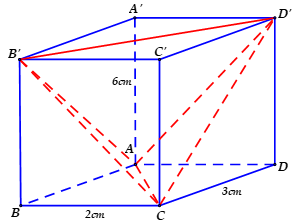
Ta có: V_{ABCD. A'B^'C^'D^'} = V_B^'.ABC + V_D^'.ACD + V_A.B^'A^'D^' + V_C.B^'C^'D^' + V_A.CB^'D'

Mà V_B^'.ABC = V_D^'.ACD = V_A.B^'A^'D^' = V_C.B^'C^'D^' =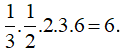

V_{ABCD.A^'B^'C^'D^'} = 2.3.6 = 36.

Chọn B.

III. BÀI TẬP ÁP DỤNG

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), SA = 3a. Thể tích khối chóp S.ABCD bằng

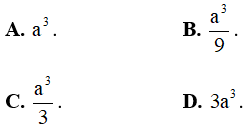
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA = AB = a, SA vuông góc với mặt phẳng (ABC). Thể tích của khối chóp S.ABC bằng

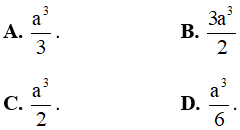
Câu 3: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và chiều cao hình chóp là a√2. Tính theo a thể tích V của khối chóp S.ABC.

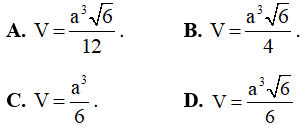
Câu 4: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = 2a, OC = 3a. Thể tích của khối tứ diện OABC bằng

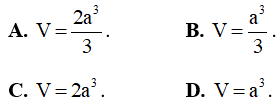
Câu 5: Cho khối lăng trụ có diện tích đáy bằng 3a² và khoảng cách giữa hai đáy bằng a. Tính thể tích V của khối lăng trụ đã cho.

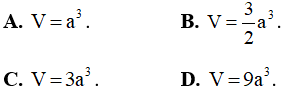
Câu 6: Khối lăng trụ có đáy là hình vuông cạnh a, đường cao bằng a√3 có thể tích bằng

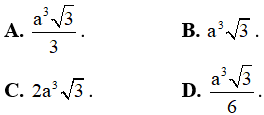
Câu 7: Cho khối lăng trụ đứng ABC.A’B’C’ có BB’ = a, đáy ABC là tam giác vuông cân tại B và AC = a√2. Tính thể tích V của khối lăng trụ đã cho.

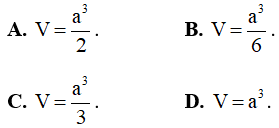
Câu 8: Thể tích khối hộp chữ nhật ABCD.A’B’C’D’ có các cạnh AB = 3, AD = 4, AA’ = 5 là

A. V = 30.

B. V = 60.

C. V = 10.

D. V = 20.

Câu 9: Cho hình hộp đứng ABCD. A’B’C’D’ có cạnh bên AA’ = h và diện tích tam giác ABC bằng S. Thể tích của khối hộp ABCD. A’B’C’D’ bằng:

Câu 10: Thể tích khối lập phương có cạnh bằng 10cm là

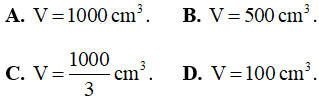
Câu 11: Cho hình hộp chữ nhật ABCD. A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’. DMN và thể tích khối hộp chữ nhật ABCD. A’B’C’D’.

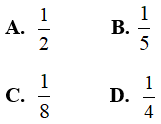
BẢNG ĐÁP ÁN