Cho 00>log b x>log a x. So sánh a,b,c ta được kết quả

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho 0<x<1; 0<a,b,c $\neq 1$ và $\log_{c} x > 0 > \log_{b} x > \log_{a} x$ . So sánh a, b, c ta được kết quả:

A. a>b>c

B. c>a>b

C. c>b>a

D. b>a>c

Trả lời:

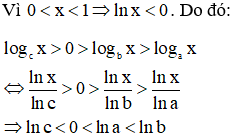
Mà hàm số $y = \ln x$ đồng biến trên $(0; + \infty)$ nên ta suy ra c<a<b

Đáp án cần chọn là: D

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Giá trị biểu thức $\log_{a} \sqrt{a \sqrt{a \sqrt[3]{a}}}$ là:

Xem lời giải »

Câu 2:

Tính $P = \frac{1}{\log_{2} 2017!} + \frac{1}{\log_{3} 2017!} + \frac{1}{\log_{4} 2017!}$ $+ . . . + \frac{1}{\log_{2017} 2017!}$

Xem lời giải »

Câu 3:

Cho $\log_{a} (\frac{\sqrt[3]{a^{7}} . a^{\frac{11}{3}}}{a^{4} . \sqrt[7]{a^{- 5}}}) = \frac{m}{n}$ với $a > 0, m, n \in N *$ và $\frac{m}{n}$ là phân số tối giản. Khẳng định nào sau đây đúng?

Xem lời giải »

Câu 4:

Cho số thực x thỏa mãn $\log_{2} (\log_{8} x) = \log_{8} (\log_{2} x)$ . Tính giá trị của $P = {(\log_{2} x)}^{2}$

Xem lời giải »

Câu 5:

Đặt $\log_{2} 3 = a; \log_{2} 5 = b$ . Hãy biểu diễn $P = \log_{3} 240$ theo a và b

Xem lời giải »

Câu 6:

Nếu $\log_{12} 18 = a$ thì $\log_{2} 3$ bằng

Xem lời giải »

Câu 7:

Cho $\log_{2} x = \sqrt{2}$ . Giá trị của biểu thức $P = \log_{2}^{2} x + \log_{\frac{1}{2}} x + \log_{4} x$ bằng

Xem lời giải »

Câu 8:

Đặt $a = \log_{2} 5$ và $b = \log_{2} 6$ . Hãy biểu diễn $\log_{3} 90$ theo a và b?

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho 00>log b x>log a x. So sánh a,b,c ta được kết quả

Xem thêm bài tập Toán có lời giải hay khác: