Cho ΔABC có hai trung tuyến CM, BN bằng nhau và cắt nhau tại G. Chứng minh tam giác ABC cân.
Câu hỏi:
Cho ΔABC có hai trung tuyến CM, BN bằng nhau và cắt nhau tại G. Chứng minh tam giác ABC cân.
Trả lời:
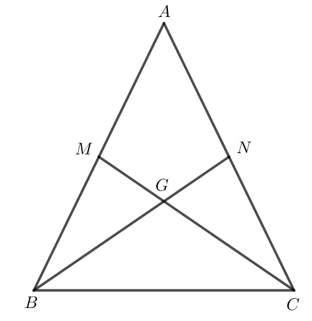
Vì G là giao điểm của hai đường trung tuyến BN và CM của tam giác ABC nên G là trọng tâm tam giác ABC.
Do đó
Mà CM = BN (giả thiết) nên CG = BG.
Δ∆BGC có CG = BG nên Δ∆BGC cân tại G.
Suy ra (tính chất tam giác cân)
Xét Δ∆BMC và Δ∆CNB có:
MC = NB (theo giả thiết),
(do )
BC là cạnh chung.
Do đó Δ∆BMC = Δ∆CNB (c.g.c).
Suy ra (hai góc tương ứng).
Tam giác ABC có nên Δ∆ABC cân tại A.
Vậy nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

