Cho alpha, beta là các số thực. Đồ thị hàm số y=x^alpha, y=x^beta trên khoảng

Câu hỏi:

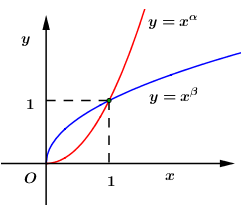
Cho $α, β$ là các số thực. Đồ thị các hàm số $y = x^{α}, y = x^{β}$ trên khoảng $(0; + \infty)$ được cho hình vẽ bên. Khẳng định nào sau đây là đúng?

A. $0 < β < 1 < α$

B. $α < 0 < 1 < β$

C. $0 < α < 1 < β$

D. $β < 0 < 1 < α$

Trả lời:

Dựa vào đồ thị hàm số ta thấy hàm số $y = x^{α}$ là hàm số đồng biến trên $(0; + \infty) \Rightarrow α > 1$

Hàm số $y = x^{β}$ nghịch biến trên $(0 : + \infty) \Rightarrow 0 < β < 1$

Vậy $0 < β < 1 < α$

Đáp án cần chọn là: A

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho $f (x) = \sqrt[3]{x} . \sqrt[4]{x} . \sqrt[12]{x^{5}}$ với $x \geq 0$ . Khi đó f(2,7) bằng

Xem lời giải »

Câu 2:

Một người gửi vào ngân hàng 100 triệu đồng với lãi suất ban đầu 4%/năm và lãi suất hàng năm được nhập vào vốn. Cứ sau một năm lãi suất tăng 0,3%. Hỏi sau 4 năm tổng số tiền người đó nhận được gần với giá trị nào nhất?

Xem lời giải »

Câu 3:

Tính đạo hàm của hàm số $y = {(2 x^{2} + x - 1)}^{\frac{2}{3}}$

Xem lời giải »

Câu 4:

Hàm số $y = \sqrt[5]{{(x^{2} + 1)}^{2}}$ có đạo hàm là

Xem lời giải »

Câu 5:

Cho hàm số $y = {(x + 2)}^{- 2}$ . Hệ thức giữa y và y’’ không phụ thuộc vào x là:

Xem lời giải »

Câu 6:

Trên đồ thị (C) của hàm số $y = x^{\frac{π}{2}}$ lấy điểm $M_{0}$ có hoành độ $x_{0} = 1$ . Tiếp tuyến của (C) tại điểm $M_{0}$ có phương trình là:

Xem lời giải »

Câu 7:

Một người gửi vào ngân hàng số tiền A đồng, lãi suất r mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn nửa năm. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau 3 năm là:

Xem lời giải »

Câu 8:

Tìm tập xác định D của hàm số $y = {(x^{3} - 6 x^{2} + 11 x - 6)}^{- 2}$

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho alpha, beta là các số thực. Đồ thị hàm số y=x^alpha, y=x^beta trên khoảng

Xem thêm bài tập Toán có lời giải hay khác: