Cho điểm O trên đường thẳng xy. Trong một nửa mặt phẳng bờ
Câu hỏi:
Cho điểm O trên đường thẳng xy. Trong một nửa mặt phẳng bờ xy ta dựng \(\widehat {zOt}\)= 90 độ. Trên Oz lấy điểm A và Ot lấy điểm B sao cho OA = OB. Kẻ AM và BN vuông góc với xy. Chứng minh rằng:
a) ∆OAM = ∆BON.
b) MN = AM + BN.
Trả lời:
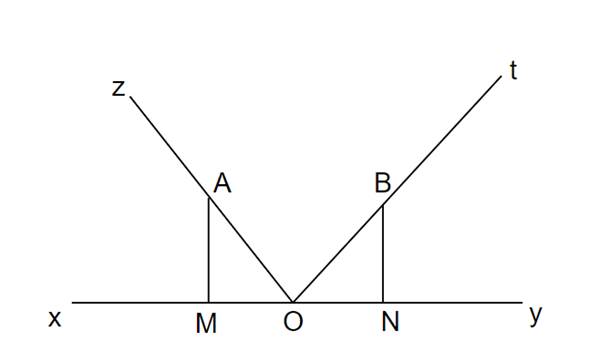
a) Ta có: \(\widehat {MOA} + \widehat {AOB} + \widehat {BON} = 180^\circ \)
Mà \(\widehat {AOB} = 90^\circ \)
⇒ \(\widehat {MOA} + \widehat {BON} = 90^\circ \)
Lại có: \(\widehat {MOA} + \widehat {OAM} = 90^\circ \)
⇒ \(\widehat {BON} = \widehat {OAM}\)
Xét ∆OAM và ∆BON có:
\(\widehat {AMO} = \widehat {BNO} = 90^\circ \)
OA = OB
\(\widehat {OAM} = \widehat {BON}\)
⇒ ∆OAM = ∆BON (g.c.g)
b) Có ∆OAM = ∆BON (phần a) nên MA = ON và OM = BN
Xét: AM + BN = ON + OM = MN
Vậy MN = AM + BN.

