Cho tam giác ABC nhọn. Đường tròn tâm O đường kính BC cắt AB ở M
Câu hỏi:
Cho tam giác ABC nhọn. Đường tròn tâm O đường kính BC cắt AB ở M và cắt AC ở N. Gọi H là giao điểm của BN và CM.
a) Chứng minh AH vuông góc với BC.
b) Gọi E là trung điểm AH. Chứng minh bốn điểm A, M, H, E cùng nằm trên một đường tròn và EM là tiếp tuyến của đường tròn (O).
Trả lời:
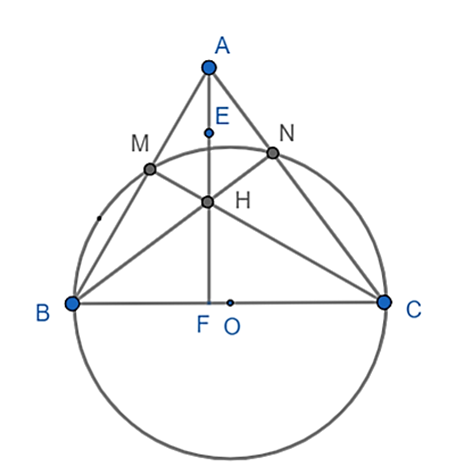
a) Xét (O) có ΔBMC nội tiếp và BC là đường kính
Do đó: ΔBMC vuông tại M
⇒ BM ⊥ MC tại M
⇒ CM ⊥AB tại M
Xét (O) có ΔBNC nội tiếp và BC là đường kính
Do đó: ΔBNC vuông tại N
⇒ BN ⊥ NC tại N
⇒ BN ⊥ AC tại N
Xét ΔABC có BN, CM là đường cao
BN cắt CM tại H
Do đó: H là trực tâm của ΔABC
⇒ AH ⊥ BC
b) Xét tứ giác AMHN có: \(\widehat {AMH} + \widehat {ANH} = 90^\circ + 90^\circ = 180^\circ \)
nên AMHN là tứ giác nội tiếp đường tròn đường kính AH
⇒A, M, H, N cùng thuộc một đường tròn.
Gọi giao điểm của AH với BC là F
Xét ΔABC có: H là trực tâm của ΔABC
F là giao điểm của AH với BC
Do đó: AH ⊥ BC tại F
⇒ ΔAFB vuông tại F
⇒ \(\widehat {ABF} + \widehat {BAF} = 90^\circ \)
Mà \(\widehat {ABF} + \widehat {MCB} = 90^\circ \)(do ΔCMB vuông tại M)
Nên: \(\widehat {MCB} = \widehat {BAF}\)
Lại có: \[\widehat {EMO} = \widehat {EMH} + \widehat {OMH} = \widehat {EMH} + \widehat {OCM} = 90^\circ - \widehat {MAH} + \widehat {MCB} = 90^\circ \]
Vậy EM là tiếp tuyến của (O).

