Cho nửa đường tròn (O). Đường kính AB = 6 cm. Kẻ các tiếp tuyến Ax

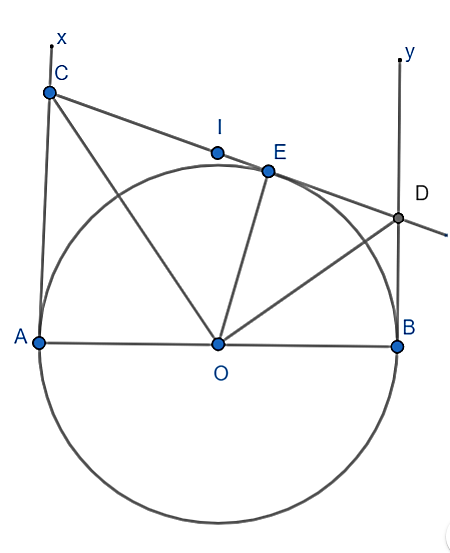
a) Ta có: \[\widehat {AOI} + \widehat {BOI} = 180^\circ \] (2 góc kề bù)

OC là tia phân giác \[\widehat {AOI}\](tính chất 2 tiếp tuyến cắt nhau)

OD là tia phân giác \[\widehat {BOI}\](tính chất 2 tiếp tuyến cắt nhau)

Suy ra: \[\widehat {ECO} = \widehat {OCA};\widehat {EDO} = \widehat {ODB}\]

Xét tam giác ACO và tam giác CEO có:

Chung CO

\[\widehat {ECO} = \widehat {OCA}\]

AC = CE (tính chất hai tiếp tuyến cắt nhau)

Nên: ∆ACO = ∆ECO (c.g.c)

⇒ \[\widehat {COA} = \widehat {COE}\]

Chứng minh tương tự, ta có: ∆DOE = ∆DOB (c.g.c)

⇒ \[\widehat {DOE} = \widehat {DOB}\]

Mà: \[\widehat {DOE} + \widehat {DOB} + \widehat {COA} + \widehat {COE} = 180^\circ \]

⇒ \[2\left( {\widehat {DOE} + \widehat {COE}} \right) = 180^\circ \]

Hay \[\widehat {DOE} + \widehat {COE} = 90^\circ \], tức \[\widehat {DOC} = 90^\circ \]

b) Ta có: \[\widehat {AEB} = \frac{1}{2}\widehat {CEO} + \frac{1}{2}\widehat {DEO} = \frac{1}{2}\widehat {DEC} = 90^\circ \]

\[\widehat {CDO} = \widehat {EBA}\](cùng chắn cung OE)

Xét ∆AEB và ∆COD có:

\[\widehat {CDO} = \widehat {EBA}\]

\[\widehat {COD} = \widehat {AEB} = 90^\circ \]

Suy ra: ∆AEB ~ ∆COD (g.g)

c) I là trung điểm của CD, kẻ IO

Ta có: DB ⊥ AB

         AC ⊥ AB

⇒ DB // AC

⇒ CDBA là hình thang 

⇒ OI là đường trung bình do nối 2 cạnh bên của hình thang

⇒ OI // AC

Mà AC ⊥ AB nên OI ⊥ AB

Vậy AB là tiếp tuyến của (I;IC)