Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N.

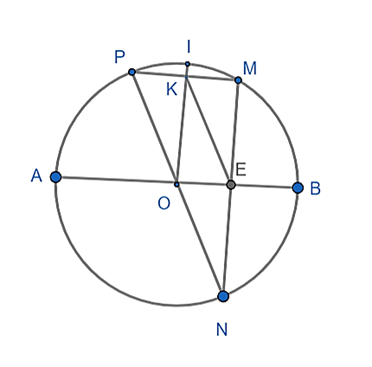
a) Xét (O) có PM // AB

⇒ 2 cung $\stackrel{⏜}{AP}$ và $\stackrel{⏜}{BM}$ bị chắn bởi 2 dây trên sẽ bằng nhau.

mà BM = BN (∆BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến)

⇒ $\stackrel{⏜}{BM}=\stackrel{⏜}{BN}$

⇒ $\stackrel{⏜}{AP}=\stackrel{⏜}{BN}$

b) Xét (O) có OI đi qua điểm chính giữa của PM (giả thiết)

⇒ OI vuông góc với dây PM tại K

⇒ $\widehat{OKM}=90°$

Xét tứ giác OKME có 3 góc vuông: $\widehat{OKM}=90°$ (cmt),

$\widehat{MEO}=90°$ ( MN vuông góc với OB tại E)

$\widehat{EMK}=90°$ (vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M)

⇒ OKME là hình chữ nhật

c) Ta có: $\widehat{OPI }=\widehat{NOE}$ (vì 2 góc đồng vị, MP//AB)

mà $\widehat{OPI }+\widehat{POI}=90°$ (∆POK vuông tại K)

⇒ $\widehat{NOE }+\widehat{POI}=90°$

⇒ $\widehat{NOE }+\widehat{POI}+\widehat{IOE}=90°+90°=180°$

⇒ P, O, N thẳng hàng

- Xét ∆PMN có KE đường trung bình (K là trung điểm PM, E là trung điểm MN)

⇒ KE//PN.