Cho tam giác ABC. Hai điểm M và N di chuyển sao cho Chứng minh MN luôn đi qua một điểm cố định.
Câu hỏi:
Cho tam giác ABC. Hai điểm M và N di chuyển sao cho . Chứng minh MN luôn đi qua một điểm cố định.
Trả lời:
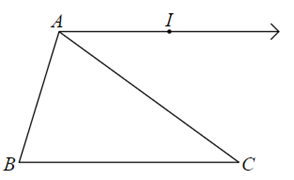
Với cách lấy điểm I như trên, ta có điểm I cố định. Khi đó MN đi qua I, thật vậy:
Theo giả thiết có:
⇒
Suy ra I là trung điểm MN hay MN đi qua I cố định.

