Cho hai số thực a, b thỏa mãn a > b > 4/3 và biểu thức
Câu hỏi:
Cho hai số thực a, b thỏa mãn và biểu thức có giá trị nhỏ nhất. Tính a + b
A.
B. 4
C. 11
D. 6
Trả lời:

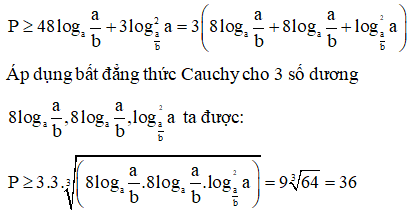

Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Biết là hai nghiệm phương trình và với a, b là hai số nguyên dương. Tính a + b
Xem lời giải »
Câu 2:
Tính tích tất cả các nghiệm thực của phương trình
Xem lời giải »
Câu 3:
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là:
Xem lời giải »
Câu 4:
Cho với và . Khi đó giá trị của m để P đạt giá trị nhỏ nhất là
Xem lời giải »
Câu 5:
Giá trị nào của m để phương trình có ít nhất 1 nghiệm thuộc đoạn
Xem lời giải »
Câu 6:
Tìm m để tồn tại duy nhất cặp (x;y) thỏa mãn và
Xem lời giải »
Câu 7:
Tìm tất cả các giá trị của m để hệ sau có nghiệm
Xem lời giải »
Câu 8:
Biết là hai nghiệm của phương trình và với a, b là hai số nguyên dương. Tính a – b.
Xem lời giải »
