Cho hình bình hành ABCD có AB = 2AD, góc D = 70 độ
Câu hỏi:
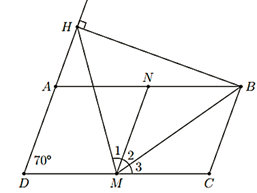
Cho hình bình hành ABCD có AB = 2AD; \(\widehat D = 70^\circ \). Vẽ BH vuông góc AD (H ∈ AD). Gọi M, N lần lượt là trung điểm cạnh CD, AB.
a) Chứng minh tứ giác ANMD là hình thoi.
b) Tính góc \(\widehat {HMC}\).
Trả lời:
Ta có:
AB // CD (tính chất hình bình hành)
N là trung điểm của AB nên AN = 1/2 AB
M là trung điểm của CD nên DM = 1/2 CD
Do AB = CD (tính chất hình bình hành) nên AN = DM
Do đó, AN // DM và AN = DM
Từ đó suy ra tứ giác ANMD là hình bình hành có hai cạnh kề bằng nhau, nên là hình thoi.
Ta có:
BH ⊥ AD (theo đề bài)
Gọi I là giao điểm của BH và MN
Ta có BI = HI (tính chất tam giác vuông cân)
Ta có MI = NI (vì M, N là trung điểm của CD, AB)
Do đó, BI = HI = MI = NI
Từ đó suy ra BH và MN giao nhau tại trung điểm I và vuông góc với nhau.
Vậy ta đã chứng minh được tứ giác ANMD là hình thoi.
b) Ta có: MN // DA và DA ⊥ BH
Suy ra: MN ⊥ BH và đi qua trung điểm của BH
Hay MN là đường trung trực của BH
⇒ \(\widehat {{M_1}} = \widehat {{M_2}}\)
Lại có: \(\widehat {{M_2}} = \widehat {{M_3}};\widehat {NMC} = \widehat {ADM} = 70^\circ \)
Suy ra: \(\widehat {{M_2}} = \widehat {{M_3}} = 70^\circ :2 = 35^\circ \)
Vậy: \[\widehat {HMC} = 3.35^\circ = 105^\circ \].

