Cho tam giác ABD có AB = 15cm, AD = 20cm, BD = 25cm
Câu hỏi:
Cho tam giác ABD có AB = 15cm, AD = 20cm, BD = 25cm. Vẽ AM vuông góc BD.
a) Chứng minh: tam giác ABD vuông. Tính AM, BM, MD.
b) Kẻ tia Bx // AD, vẽ AM vuông góc BD cắt Bx tại C. Chứng minh: AB2 = AD.BC.Trả lời:
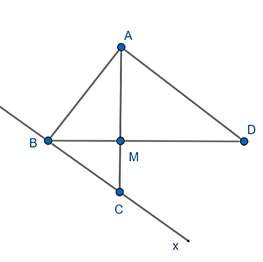
a) Ta thấy: 252 = 202 + 152 hay AB2 + AD2 = BD2
Theo định lí Pytago đảo, suy ra tam giác ABD vuông tại A
Áp dụng hệ thức lượng trong tam giác ABD vuông ta có:
AB.AD = AM.BD ⇒ AM = \(\frac{{AB.AD}}{{BD}} = \frac{{15.20}}{{25}} = 12cm\)
AD2 = MD.BD ⇒ DM = \(\frac{{A{D^2}}}{{BD}} = \frac{{{{20}^2}}}{{25}} = 16cm\)
BM = BD – DM = 25 – 16 = 9(cm)
b) Vì AB ⊥ AD do ABD vuông tại A
Và Bx // AD
Nên Bx ⊥ AB tại B. Suy ra: \(\widehat {ABC} = 90^\circ \)
Xét tam giác BAM và tam giác BDA có:
Chung \(\widehat B\)
\(\widehat {BMA} = \widehat {BAD} = 90^\circ \)
⇒ ∆BMA ∽ ∆BAD (g.g)
Suy ra: \(\widehat {BAM} = \widehat {BDA}\) hay \(\widehat {BAC} = \widehat {BDA}\)
Xét tam giác BAC và tam giác BAD có:
\(\widehat {BAC} = \widehat {BDA}\)(chứng minh trên)
\(\widehat {ABC} = \widehat {BAD} = 90^\circ \)
⇒ ∆BAC ∽ ∆ADB (g.g)
⇒ \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\) ⇒ AB2 = AD.AC.

