Cho hình bình hành ABCD. Vẽ về phía ngoài hình bình hành
Câu hỏi:
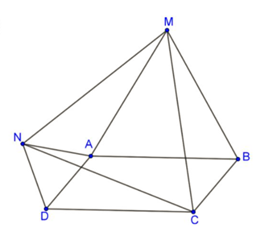
Cho hình bình hành ABCD. Vẽ về phía ngoài hình bình hành các tam giác đều ABM, AND. Gọi E, F, Q theo thứ tự là trung điểm của BD, AN, AM. Hỏi tam giác MNC là tam giác gì? Vì sao?
Trả lời:
\(\widehat {MBC} = \widehat {MBA} + \widehat {ABC} = 60^\circ + \widehat {ABC}\left( 1 \right)\)
\(\widehat {CDN} = \widehat {NDA} + \widehat {ABC} = 60^\circ + \widehat {ABC}\left( 2 \right)\)
\(\widehat {MAN} = 360^\circ - \widehat {MAB} - \widehat {NAD} - \widehat {BAD}\)
\(\widehat {MAN} = 360^\circ - 60^\circ - 60^\circ - \widehat {BAD} = 240^\circ - \left( {180^\circ - \widehat {ABC}} \right) = 60^\circ + \widehat {ABC}\left( 3 \right)\)
Từ (1), (2), (3): \(\widehat {MBC} = \widehat {CDN} = \widehat {MAN}\)
Xét tam giác MBC và tam giác CDN có:
BC = DN (=AD)
\(\widehat {MBC} = \widehat {CDN}\)
MB = DC (=AB)
⇒ ∆MBC = ∆CDN (c.g.c)
Chứng minh tương tự: ∆MBC = ∆MAN (c.g.c)
⇒ ∆MBC = ∆CDN = ∆MAN
⇒ MC = CN = MN
⇒ Tam giác CMN là tam giác đều.

