Cho hình chóp đều S. ABCD có AC = 2a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD)

Câu hỏi:

Cho hình chóp đều S. ABCD có AC = 2a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD) bằng 45⁰. Tính thể tích V của khối chóp S.ABCD theo a.

A. $V = \frac{a^{3} \sqrt{2}}{3}$

B. $V = \frac{2 a^{3} \sqrt{3}}{3}$

C. $V = a^{3} \sqrt{2}$

D. $V = \frac{a^{3}}{2}$

Trả lời:

Chọn A

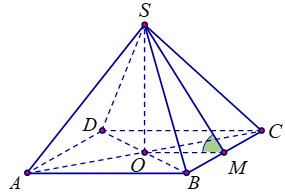
Gọi M là trung điểm của BC, suy ra $O M ⊥ B C$ .

Ta có $\hat{(S B C); (A B C D)} = \hat{S M O} = 45^{o}$ .

Ta có

$A C^{2} = A B^{2} + B C^{2} = 4 a^{2} \Rightarrow A B = B C = a \sqrt{2} . O M = \frac{1}{2} A B = \frac{a \sqrt{2}}{2} \Rightarrow S O = \frac{a \sqrt{2}}{2} . \tan 45^{o} = \frac{a \sqrt{2}}{2}$ .

Vậy $V_{S . A B C D} = \frac{1}{3} . S O . S_{A B C D} = \frac{1}{3} . \frac{a \sqrt{2}}{2} . {(a \sqrt{2})}^{2} = \frac{\sqrt{2} a^{3}}{3}$ .

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, $\hat{B A C} = 120^{o}$ và BC =AA' = a $\sqrt{3}$ . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.

Xem lời giải »

Câu 2:

Cho khối lăng trụ tam giác đứng ABC.A'B'C' có đáy là tam giác vuông tại A, AC = AB = 2a, góc giữa AC' và mặt phẳng (ABC) bằng 30⁰. Tính thể tích của khối lăng trụ ABC.A'B'C'.

Xem lời giải »

Câu 3:

Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 45⁰.

Xem lời giải »

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh $a \sqrt{3}$ . Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SC=4a. Tìm thể tích khối chóp S.ABCD.

Xem lời giải »

Câu 5:

Cho khối lăng trụ đứng, mặt phẳng (P) đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ ABC. A'B'C' thành hai khối đa diện có tỷ số thể tích bằng k với k ≤ 1. Tìm k.

Xem lời giải »

Câu 6:

Cho khối chóp S. ABC có góc $\hat{A S B} = \hat{B S C} = \hat{C S A} = 60^{o}$ và SA=2, SB=3, SC=4. Thể tích khối chóp S. ABC.

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho hình chóp đều S. ABCD có AC = 2a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD)

Xem thêm bài tập Toán có lời giải hay khác: