Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông
Câu hỏi:
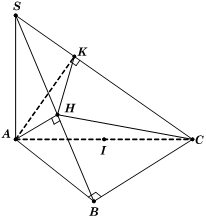
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Thể tích của khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKCB là:
A.
B.
C.
D.
Trả lời:
Chọn A
Theo giả thiết, ta có và (1)
Do (2)
Từ (1) và (2), suy ra ba điểm B, H, K cùng nhìn xuống AC dưới một góc 90o nên hình chóp A.HKCB nội tiếp mặt cầu tâm I là trung điểm AC, bán kính
Vậy thể tích khối cầu
(đvtt).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho đường tròn (C) đường kính AB và đường thẳng . Để hình tròn xoay sinh bởi (C) khi quay quanh là một mặt cầu thì cần có thêm điều kiện nào sau đây:
(I) Đường kính AB thuộc .
(II) cố định và đường kính AB thuộc .
(III) cố định và hai điểm A, B cố định trên .
Xem lời giải »
Câu 2:
Cho mặt cầu (S) tâm O, bán kính R và mặt phẳng (P) có khoảng cách đến O bằng R. Một điểm M tùy ý thuộc (S). Đường thẳng OM cắt (P) tại N. Hình chiếu của O trên (P) là I. Mệnh đề nào sau đây đúng?
Xem lời giải »
Câu 3:
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
Xem lời giải »
Câu 4:
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một cát tuyến cắt (S) tại B và C sao cho . Khi đó khoảng cách từ O đến BC bằng:
Xem lời giải »
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng 60o . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD nhận giá trị nào sau đây?
Xem lời giải »
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là trung điểm H của cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60o . Gọi G là trọng tâm tam giác SAC , R là bán kính mặt cầu có tâm G và tiếp xúc với mặt phẳng (SAB) . Đẳng thức nào sau đây sai?
Xem lời giải »
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là:
Xem lời giải »
Câu 8:
Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a. Cạnh bên và vuông góc với đáy (ABC). Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
Xem lời giải »