Cho hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A. cạnh BC=2a và
Câu hỏi:
Cho hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A. cạnh BC=2a và nhọn. Biết (BCC'B') vuông góc với (ABC) và (ABB'A') tạo với (ABC) góc 450. Thể tích của khối lăng trụ ABC. A'B'C' bằng:
A.
B.
C.
D.
Trả lời:
Chọn B
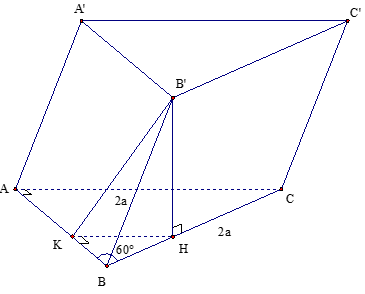
Do ABC là tam giác vuông tại A, cạnh BC=2a và nên AB=a, AC=√3
Gọi H là hình chiếu vuông góc của B' lên BC => H thuộc đoạn BC (do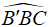 
nhọn)
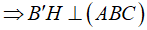(do (BCC'B') vuông góc với (ABC)).
Kẻ HK song song AC (K thuộc AB)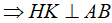 
(do ABC là tam giác vuông tại A).
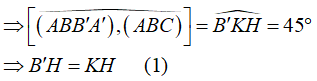
Ta có ΔBB'H vuông tại H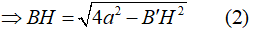 
Mặt khác HK song song AC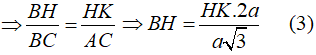 
Từ (1), (2) và (3) suy ra:
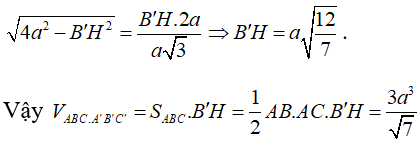
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a.
Xem lời giải »
Câu 2:
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD). Biết côsin của góc tạo bởi mặt phẳng (SCD) và (ABCD) bằng . Thể tích Vcủa khối chóp S.ABCD là:
Xem lời giải »
Câu 3:
Khối chóp S.ABCD có đáy là hình thoi cạnh a, SA = SB = SC = a, cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S.ABCD là:
Xem lời giải »
Câu 4:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng:
Xem lời giải »
Câu 5:
Cho khối lăng trụ ABC. A'B'C'. Gọi E là trọng tâm tam giác A'B'C' và F là trung điểm BC. Tính tỉ số thể tích giữa khối B'. EAF và khối lăng trụ ABC. A'B'C'.
Xem lời giải »
Câu 6:
Cho hình chóp S. ABC có đường cao SA=2a, tam giác ABC vuông tại C, AB=2a,. Gọi H là hình chiếu của A trên SC, B' là điểm đối xứng của B qua mặt phẳng (SAC). Thể tích của khối chóp H. AB'B bằng:
Xem lời giải »
