Cho số phức z có acgumen là phi. Tìm một acgumen của số phức z ngang
Câu hỏi:
Cho số phức z có acgumen là . Tìm một acgumen của số phức
A.
B.
C.
D.
Trả lời:
Đáp án D
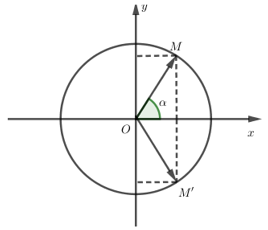
Số phức z có điểm biểu diễn là M thì có điểm biểu diễn là M’ đối xứng với M qua Ox. Do đó là một acgumen của
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Số phức z có mô đun r = 3 và acgumen thì có dạng lượng giác là:
Xem lời giải »
Câu 2:
Phần thực của số phức z thỏa mãn là:
Xem lời giải »
Câu 3:
Điểm biểu diễn của số phức z là M(1;2). Tọa độ của điểm biểu diễn số phức là:
Xem lời giải »
Câu 4:
Gọi lần lượt là hai nghiệm của phương trình với có phần ảo dương. Giá trị của biểu thức bằng
Xem lời giải »
Câu 5:
Giả sử là hai nghiệm phức của phương trình và A, B là các điểm biểu diễn của . Tọa độ trung điểm của đoạn thẳng AB là:
Xem lời giải »
Câu 6:
Cho số phức . Chọn 1 acgumen của z:
Xem lời giải »
Câu 7:
Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện |z| = 5,
Xem lời giải »
Câu 8:
Gọi là 1 acgumen của số phức z có điểm biểu diễn là nằm trên đường tròn đơn vị, số đo nào sau đây có thể là một acgumen của z?
Xem lời giải »


